SCI论文(www.lunwensci.com)
摘要:“解决实际问题”是小学数学的“亮点”,集中反映了学生的基础知识水平、数学思维水平,以及知识应用能力,属于一项综合性考察题目。在《义务教育数学课程标准(2022年版)》(以下简称“新课标”)中,也对“解决实际问题”提出了更加具体的要求,倡导教师基于“解决实际问题”这一载体,借助多元化教学模式,全面激活学生的数学思维,提升数学知识应用能力。本文以此切入,分析了“解决实际问题”的教学现状,并结合教学实践案例,对“解决实际问题”教学策略展开探究,旨在提高数学课堂的教学效果。
[关键词]核心素养,小学数学,解决实际问题,教学策略
“解决实际问题”的前身是应用题,是小学数学的重要组成部分,也是教学重难点。新课标对“解决实际问题”提出了更高的要求,要求能够综合数学知识,从数学的角度发现问题、分析问题、解决问题,提升学生的数学应用意识,培养学生多样化解决问题的能力,使其在一题多解中发散思维,并形成一定的创新意识。传统的应用题教学模式显然已经无法满足“解决实际问题”的教学需求。鉴于此,小学数学教师唯有精准把握新课标下“解决实际问题”的要求,基于小学生的实际情况,积极探索一套全新的教学模式,旨在提升学生解决实际问题的能力。
一、核心素养下小学数学“解决实际问题”新要求
在2001年颁布并开始实验的《全日制义务教育数学课程标准(实验稿)》中,首次提出了“解决问题”这一目标,随即成为小学数学课堂教学“四大目标”之一。伴随新课程改革的深入推进,关于“解决实际问题”的要求持续完善。在新课标中,聚焦“解决实际问题”的要求,进行了详细的阐述:引领学生综合数学知识,从数学的角度分析问题、解决问题;引领学生在运用数学知识解决实际问题的过程中,发散思维、增强应用意识,并提升学生的实践能力。分别从低、中、高学段提出了“解决实际问题”新要求,如(1)低学段:初步掌握和运用加法、减法、乘法、除法解决实际问题的能力,能够列出解决两步计算问题的分步解决方案。(2)中学段:能够列等式解答两步或者相对容易的三步计算类型的问题;掌握常见的数量关系。掌握并理解解决实际问题的一般步骤。(3)高学段:能够运用方程、比例等知识,解决实际生活中的工程问题、分数问题、比例问题等。
二、核心素养下小学数学“解决实际问题”教学策略研究
(一)优化审题教学,读懂题目含义
鉴于“解决实际问题”的内涵,教师在开展教学时,最为重要的就是加强审题教学,带领学生认真审题,读懂读透题目、明确问题。首先,教师必须要引导学生一字不落地读题,认真看清楚题目中的每一个字、每一句话。同时,还应在阅读中,圈出关键词,提炼出已知条件,分析所求问题。其次,教师必须要指导学生认真阅读题目,通过仔细分析,深层次挖掘题目中的隐含条件,排除干扰条件。最后,在“解决实际问题”审题中,还应通过题目明确其考查的知识点,从数学知识体系中找到对应知识点,进而形成针对性的解题思路。
例如,在对“红红摘了20个苹果,姐姐比红红多摘了10个苹果,两个人一共摘了多少个苹果?”这一题目进行审题时,先指导学生一字不落地阅读题目,之后再将关键词“姐姐比红红多”“一共”标注出来,并引导学生一边审题一边思考:姐姐摘了多少个?两个人一共摘了多少?如此,在教师的引导下,学生通过认真审题,基本上弄懂了题目的意思,为其更好地解答问题奠定了坚实的基础。
(二)分析题目,厘清数量关系
数学本身就是一门研究数量关系、空间形式的科学,数量关系反映了某些数量之间的本质联系,是解决数学问题的“金钥匙”。无论是哪一个类型的题目,学生要想完成题目的解答,不仅要认真审题,还要厘清题目中的数量关系,找到条件和问题之间的联系。只有在此基础上,才能运用数量关系,从已知转换到未知,最终实现问题的解答。鉴于此,教师在日常教学中,应有意识地引导学生去分析题目、寻找题目中的数量关系,并加强技能指导,指导学生采用画图或者列表的方式,将题目中的数量关系呈现出来。
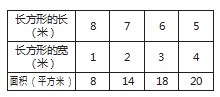
例如,“王叔叔打算用一个18m长的栅栏围成一块长方形的菜地,请问有多少种围法?在周长不变的情况下,哪一种围法使王叔叔得到的菜地面积最大?”针对这一题目,教师在引导学生分析、解答题目时,为帮助学生更好地厘清题目中的数量关系,可以指导学生一边审题,一边绘制表格,将题目中的数量关系清晰地呈现出来(见下表)。借助表格将题目中的数量关系清晰地呈现出来。学生只要结合所学的数学知识,即可轻松得出第一问的答案,即有4种。同时,学生通过观察图表还可以发现,长方形长和宽的差距越小,面积就越大。因此,当长为5米、宽为4米时,所围成的长方形面积最大,为20平方米。
(三)开展一题多解训练,强化解题思维
鉴于“解决实际问题”的教学要求,教师在优化课堂教学时,必须要改变传统“重结果、轻过程”的观念,全面加强小学生的思维训练。而要达到这一目标,一题多解训练是最佳的选择。这主要是因为通过一题多解训练,可强化学生思维的连贯性、灵活性、发散性,促进高阶思维的发展。另外,学生在多角度分析问题、解决问题的过程中,也能深刻理解基本的数学概念、数学公式,促进了知识的迁移和融会贯通,真正提升了学生的数学综合能力。鉴于此,教师在日常课堂教学中,必须要结合实际情况,带领学生积极开展“一题多解”训练。
例如,“两辆车同时从甲乙两地出发,相对而行。出发两个小时之后,两辆车相遇。其中一辆车的速度为30千米/时,另一辆车的速度是35千米/时。则甲乙两地的距离是多少?”这是一道非常典型的行程问题,是对学生进行思维训练的最佳切入点。教师可引导学生结合所学的数学知识,从多个角度进行思考、解答,最终在“一题多解”训练中,促进数学思维的发展,并拓展数学解题思路。
解法一:引导学生根据题目中已知条件展开思考、分析,先求出两者相遇时,两辆车各自走的路程,之后再将其加起来,即为总路程:30×2+35×2=130(千米)。
解法二:引导学生根据题目中已知条件,先计算出两辆车每个小时一共行驶的路程,之后再乘以相遇的时间,即可计算出两地的路程,即:(30+35)×2=130(千米)。
解法三:根据题目中已知条件和所求结论,可融入方程思想进行解答。假设两地之间的距离为x千米,除以两车相遇的时间,即为两辆车的速度和:x÷2=30+35,解方程得x=130。
(四)渗透数学思想,强化解题能力
数学思想是“解决实际问题”的核心,常常蕴含在数学解题策略中。鉴于新课标下“解决实际问题”的教学要求,在日常教学中,教师不能局限于技术层面,还应积极渗透数学思想,指导学生在数学解题中感悟其中蕴含的数学思想,并逐渐掌握和运用数学思想解答问题的技能。在小学数学学习中,数形结合思想的应用尤为普遍,尤其是针对一些难度比较大、数量关系复杂的数学问题,可融入数形结合思想,引导学生一边审题、一边绘制相关的图形,最终在数形结合思想的辅助下,形成明确的解题思路。
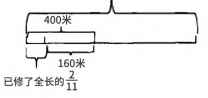
例如,“修一条公路,第一天修了全程的,第二天又修了160米。已知前两天一共修了400米。问:这条公路全长多少米?”这是数学学科中常见的一道工程问题,由于题目中涉及分数、具体的路程等,数量关系相对比较复杂,为学生的解题带来了极大的难度。鉴于此,在指导学生解题时,即可运用数形结合思想,引导学生一边审题,一边绘制线段图(见图1)。如此,题目中的数量关系一目了然,学生即可从中得出解题的思路:两天修的全长(400米)-第二天修的全长(160米)=第一天修的全长。而第一天修的全长是整条路的400-160=240(米),240÷11=1320(米)。可以说,在本题中,通过线段图(见下图),使得题目中的数量关系更加简单明了,以便于学生快速找到解题的“突破口”。除此之外,在小学数学解题中,转化思想也是比较常见的。所谓的转化思想,就是将一个问题进行转化,使其成为另外一个问题,并运用相关的知识进行解答。经过课堂教学实践证明,在小学数学课堂教学中,应用转化思想,能够彻底打开小学生的数学解题思路,并在转化中形成系统的知识体系。
例如,“一根钢管长2.7米,截下全长的,加工了9个零件。那么剩下的钢管还能做多少个零件?”在解决这一道数学题目时,即可引导学生融入转化思想,从不同的角度进行思考,寻找不同的解题方法。
解法一:根据题目含义,可将其与工程问题联系在一起,将整个钢管的长度视为单位“1”。如此,题目即可转化为工程问题,形成解题思路(1-
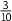
)÷(

÷9)=21;
解法二:根据题目意思,还可以将其转化成为所学的“倍比问题”,假设整个钢管为“10份”,已经做了3份,余下7份未做,则根据倍比关系,得出余下份数占已加工份数的7÷3=倍,由于3份做了9个零件,因此余下份数可做7÷3×9=21(个)。
可见,在这一数学题目中,就是运用了转化思想,引导学生从工程、倍比两个角度进行思考、分析、解答。如此,不仅拓展了学生的解题思路,也促使其在解题中形成了系统的数学知识体系,真正提升了学生的数学综合素养。
(五)融合同一类型问题,强化解题能力
“解决实际问题”能力不是一朝一夕就能形成的,必须要在教师的引导下,通过长期的针对性训练,方可达到预期的目标。鉴于“解决实际问题”千变万化的现状,教师需要灵活应用探究式教学模式,为学生留出适当的空间、时间,通过启发、鼓励、引导等方式,指导学生对同一类型的题目进行整合、分析,使其在同一类型题目的探究中,循序渐进地提升自身的解题能力。
例如,在学习完“植树问题”之后,就以“某绿化要在一条长度为150m的小路一边植树,每隔10m种一棵树,并且两端都要栽种,一共要栽种多少棵树?”为例,将“一端种树、两端都不种”的相关题目给学生呈现出来,使得学生在同一类型数学题目的对比学习中,真正理解植树问题的三种模型:(1)两端都种,总长÷间隔=段数,段数+1=棵数;(2)只栽种一端,总长÷间隔=段数,段数=棵数;(3)两端都不种,则总长÷间隔=段数,段数-1=棵数。在此基础上,教师对这一类型的问题进行了拓展和延伸,包括:锯木头问题、公交车站点问题、爬楼问题、敲钟问题等进行了整合,使得学生在“植树问题”的拓展和延伸中,真正掌握这一类型题目的内涵本质,丰富了这一类型题目的解答方式。
(六)鼓励学生自行创编题目
在开展“解决实际问题”的教学中,教师要彻底摒除“题海战术”的模式,给学生提供独立思考、拓展延伸的平台,引导学生结合所学知识,自行创编题目。小学阶段所涉及的“解决实际问题”类型,主要包括浓度问题、行程问题、分数问题、植树问题、年龄问题等。鉴于此,在日常教学过程中,可为学生搭建一个自由创编的平台,引导学生在自编题目、自己解决的过程中,真正掌握某一个部分的知识点。
例如,在“比例尺”相关知识教学中,笔者就聚焦这一部分知识点,为学生设计了一个问题:“在一张1:800的图纸中,某长方形面积为560cm2,周长为120cm,则该长方形的实际面积为多少?周长为多少?”这一问题比较简单,在教师的引导下,学生可轻松解答。接着,教师指导学生参考例题,结合自己的实际生活自行创编题目。如此,学生在创编题目的过程中,真正掌握了某一类型题目的内涵,提升了学生的实际问题解决能力。
综上所述,核心素养视域下,对小学数学“解决实际问题”教学提出了更高的要求。鉴于此,小学数学教师唯有转变传统的教学观念与模式,根据新课标的要求,立足于小学生的实际情况,从审题、数量关系分析、数学思维、数学思想等维度优化教学,不断提升学生的审题能力、问题分析能力和数学思维等,以便于其能够灵活运用所学知识,解决各类实际问题。
参考文献:
[1]吴顺田.基于核心素养的小学数学解决问题教学研究[J].亚太教育,2022(14):54-56.
[2]台芳芳.核心素养背景下小学数学“解决实际问题”的教学策略研究[J].数学学习与研究,2021(13):113-114.
[3]顾雯婷.小学低年级数学解决实际问题教学策略的研究[J].文理导航(下旬),2021(1):40+47.
[4]马小花.锻造思维品质促进学习真的发生——小学数学“解决实际问题”指导策略探究[J].教育实践与研究(A),2020(10):30-32.
[5]高晨.核心素养下小学数学“问题解决”的教学研究[D].厦门:集美大学,2019.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/72243.html
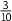 )÷(
)÷( ÷9)=21;
÷9)=21;