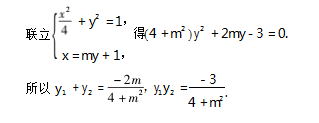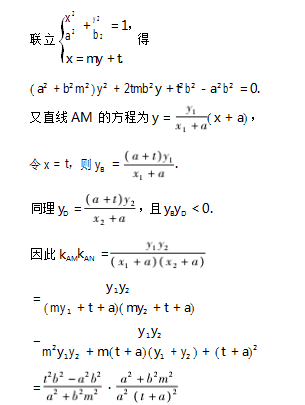SCI论文(www.lunwensci.com)
摘 要 : 文章给出了一道 2021 年清华大学强基计划试题的多种解法,并对试题进行推广探究.
关键词 : 清华大学,强基计划,试题推广
文[1]给出了 2021 年清华大学强基计划数学 试题的解答,其中第 11 题从学生惯用的斜率 k 入手 设参求解,不论是定值的求解还是最值的取得,都忽 略了斜率不存在的情况,这也正是学生解题时容易 疏漏的地方.笔者对文[1]的解答做出了改进,并探 究试题的其他解法及推广,以开阔学生的解题视野,构建知识体系,探寻试题本质规律.
1 试题呈现
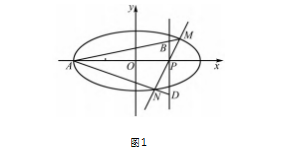
P( 1.0 ) 的直线交椭圆与 M,N 两点,直线 AM,AN 与 直线 x = 1 分别交于 B,D 两点,则下列选项正确的 是( ) .
A.PB·PD为定值
B.PB+PD为定值
C.PB· 1|PD 的值可以是 2
D.PB+PD的值可以是 2
分析 如图 1.试题以椭圆 C 与过其长轴上一定点的动直线交于 M,N 两点为背景,设计了与之相关的定值、最值问题的探究,解题的关键在于几何关 系PB·PD 1 1.PB +PD如何转化为坐标运 算,而直线 AM,AN,MN 的内在联系为考生构图设参 提供了丰富的视角.问题的设计给广大考生充分发 挥自己能力的空间,有助于创新人才和拔尖人才的选拔.
2 解法分析
解法 1 由题设知直线 MN 的斜率不为 0.因此 设直 线 MN 的 方 程 为 x = my + 1.M ( x1 ,y1 ) ,N( x2 ,y2 ) .
因此,选项 A,D 正确,B,C 错误.
点评 该解法与文[1]的解法都是从直线 MN 入手构图设参,将所求几何问题转化为点 B 与点 D 纵坐标的相关运算,区别在于直线 MN 的表达,该解 法中直线 MN 的方程用 x = my + 1 的设法回避了讨 论斜率的存在性,避免了解题时因斜率不存在的情况而造成的疏漏.
解法 2 记直线 AM,AN 在 y 轴上的截距分别
点评 该解法从直线AM,AN 入手构图设参,亮 点在于抓住了直线 AM 与 AN 逻辑结构的对称性,巧 妙地利用直线方程的截距式设参求解,不仅简化了 数学运算,还发现了直线 AM 与 AN 在 y 轴上的截距 之积 mn 为定值这一规律,为进一步揭示试题本质提供了思考途径.
点评 该解法从形入手,利用几何关系将所求 问题BP·DP转化为两直线 AM 与 AN 的斜率之积 k1 k2 的代数运算,从而问题最终落在了点 M 与N 的坐标表达上,该解法在设点时选择了椭圆的参 数方程,从参数的视角阐释了直线 MN 在运动变化过程中保持的规律性,与解法2 揭示的规律相得益彰.
解法 4 由题设知直线 AM,AN 的斜率均存在,故设直线 AM,AN 的方程分别为
点评 单墫教授在《解析几何的技巧》中写道 “将两个一次方程乘起来是一个重要的手法,在组 成二次曲线束时常常需要这样做 ” ,这也是该解法 的特点.站在曲线系的视角,这类问题的解答显得更为简洁、高效,试题所揭示的规律也更为清晰、直白.
上述四种解法从不同侧面阐释了过点P( 1.0 ) 的直线 MN 在运动变化过程中保持的规律性,即直 线 AM 与 AN 斜率之积为定值,并在这一规律基础上衍生了相关定值、最值.同时,也给了我们继续深入探究试题本质的启发与思考.
3 推广探究
思考 1 若试题中的点 P ( 1.0 )一般化为长轴上异于顶点的任一点 P( t,0 ) ,结论还是否成立?经探究,得到如下结论 :
对于双曲线,为了保持和椭圆具有统一的规律 性,此处只推广直线交双曲线于同一支的情形,证明过程如变式 1 的解法,不再赘述.
变式 2 已知抛物线 y2 = 4x 的顶点为 O,过点 P( 2.0 ) 的直线交抛物线于 M,N 两点,直线 OM,ON与直线 x = 2 分别交于 B,D 两点,
( 1) 求证 :PB·PD为定值 ;
(2) 求PB+PD的最小值.
经由上述解法探索、变式思考和推广探究,试题 的本质逐渐显现,解题活动也由对解法的初步探索 逐步深化到对试题的领悟和对数学的理解,正如罗 增儒教授所讲的解题的四个水平在不断深入探究中 得以展开.在强基计划实施的当下,深入挖掘试题价值,对培养学生的解题能力和创新能力大有裨益.
参考文献 :
[1]甘志国.2021 年清华大学强基计划数学试题及 其详解[J].数理化解题研究,2022 (04) : 88 -89 .
[2]管良梁.立足经验生长 实现解答自然——— 以 一道解析几何定值问题的教学为例[J].数理 化解题研究,2022 (22) : 89-91 .
[3] 田鹏.一道椭圆中两线段长度乘积为定值试题 的探究[J].数理化学习( 高中版) ,2022 (06) :15 -18 .
[4]周文国.解析几何中定值定点问题的解决策略[J].理科考试研究,2020.27 (15) : 17-20 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/71480.html