SCI论文(www.lunwensci.com)
摘要:解三角形是高考解答题的热点题型,求解此类问题需要分析已知条件,合理运用正弦定理和余弦定理构建边和角的关系.在处理三角形中的边角关系时,一般都化为角的关系,或都化为边的关系.题中若出现边的一次式一般运用正弦定理,出现边的二次式一般运用余弦定理.解决三角形问题时还要注意角的限制范围.
关键词:解三角形,正弦定理,余弦定理
1试题呈现
题目(2020年全国Ⅰ卷文数第18题)ΔABC的内角A,B,C的对边分别为a,b,c.已知B=150°.
(1)若a=
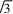
,b=2
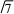
,求ΔABC的面积;(2)若sinA+
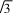
sinC=
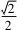
,求C.2试题探析
2.1第(1)问解析
解法1由余弦定理可知b2=a2+c2-2accosB.故28=3c2+c2-2
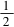
3 c·ccos150.所以7c2=28,解得c2=4.所以ΔABC的面积为S=acsinB=c2=
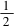
解法2由正弦定理可知a=
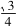
c⇔sinA=
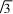
sinC.由B=150°,得A+C=30°所以03 sinC=sinA=sin(30°-C)=cosC-
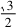
sinC.所以cosC=3sinC.由sin2 C+cos2 C=1,sinC>0,得sinC=1.
2
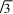
7由正弦定理知siC=siB.所以c=bs=2.从而a=2
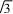
所以ΔABC的面积为S=acsinB=
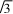
解法3由余弦定理可知
b2=a2+c2-2accosB.故28=3c2+c2-2
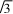
c·ccos150.所以7c2=28,解得c=2.从而a=2
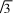
3.所以ΔABC的面积为S=
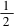
acsinB=
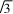
解法4如图1,过点C作CD⊥BA,交AB的延长线于点D,依题意可得CD=a=c,BD=
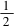
CD=c.
在RtΔADC中,由勾股定理可得CD2+AD2=AC2.所以c2+c2=28.解得c2=4.所以ΔABC的面积为S=acsinB=c2=
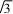
解法5如图2,过点B作BD⊥AC于点D,设∠ABD=θ,则∠CBD=150°-θ.
依题意得CD=asin(150°-θ)=一道高考题的多解分析论文csin(150°-θ),AD=csinθ,BD=一道高考题的多解分析论文ccos(150°-θ)=ccosθ⇔
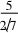
一道高考题的多解分析论文sinθ=5cosθ.结合sin2θ+cos2θ=1可得sinθ=
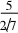
,cosθ=.
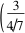
由AD+CD=AC=2一道高考题的多解分析论文,得一道高考题的多解分析论文csin(150°-θ)+csinθ=cosθ+sinθ)c=2一道高考题的多解分析论文.所以+)c=
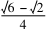
,解得c=2.从而a=.
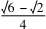
所以ΔABC的面积为S=acsinB=一道高考题的多解分析论文.
2.2第(2)问解析
解法1因为B=150°,从而A+C=30°.故sinA+一道高考题的多解分析论文sinC=sin(30°-C)+一道高考题的多解分析论文sinC=cosC-一道高考题的多解分析论文sinC+一道高考题的多解分析论文sinC=2 cosC+一道高考题的多解分析论文2 sinC=sin(C+30°)=.
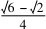
因为0°<C<30°,从而30°<C+30°<60°.所以C+30°=45°,解得C=15°.
解法2因为B=150°,从而A+C=30°.故sinA+一道高考题的多解分析论文sinC=sin(30°-C)+一道高考题的多解分析论文sinC=cosC-sinC+一道高考题的多解分析论文sinC
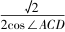
=cosC+sinC=.
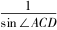
所以cosC=一道高考题的多解分析论文-一道高考题的多解分析论文sinC.
因为sin2 C+cos2 C=1,所以sin2 C+(一道高考题的多解分析论文-一道高考题的多解分析论文sinC)2=4sin2 C-2一道高考题的多解分析论文sinC+2=1,解得sinC=.
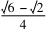
因为0°<C<30°,所以sinC=.
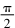
又因为sin15°=,所以C=15°.
解法3因为B=150°,从而A+C=30°.故sinA+一道高考题的多解分析论文sinC=sinA+一道高考题的多解分析论文sin(30°-A)=sinA+cosC-sinA=cosA-sinA=sin(60°-A)=.
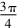
因为0°<C<30°,从而30°<60°-A<60°.所以60°-A=45°,解得A=15°.从而C=15°.
解法4因为B=150°,从而A+C=30°.
故sinA+一道高考题的多解分析论文sinC=sin(30°-C)+一道高考题的多解分析论文sinC=cosC-sinC+一道高考题的多解分析论文sinC=cosC+sinC=sinBcosC-cosBsinC=sin(150°-C)=.
因为0°<C<30°,从而120°<150°-C<150°.所以150°-C=135°,解得C=15°.解法5因为sinB=,故sinA+一道高考题的多解分析论文sinC=一道高考题的多解分析论文sinB.
由正弦定理,得a+一道高考题的多解分析论文c=一道高考题的多解分析论文b⇔b=.
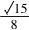
由余弦定理,得b2=a2+c2-2accos150°.所以()2=a2+c2+一道高考题的多解分析论文ac.
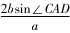
即a2=b2,故a=c,从而A=C.因为A+C=180°-B=30°,所以C=15°.
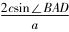
解法6因为sinB=,
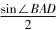
故sinA+一道高考题的多解分析论文sinC==一道高考题的多解分析论文sinB.由余弦定理,得b2=a2+c2-2accos150°.由正弦定理,得sin2 B=sin2A+sin2 C+一道高考题的多解分析论文3 sinA·sinC.故()2=sin2A+sin2 C+一道高考题的多解分析论文sinAsinC.所以sin2A=sin2 C.因为0°<A,C<30°,故sinA=sinC.从而A=C.因为A+C=180°-B=30°,所以C=15°
3同类变式
题1在锐角ΔABC中,角A,B,C的对边分别为a,b,c,已知sin(A-B)=cosC.
(1)若a=3一道高考题的多解分析论文,b=一道高考题的多解分析论文,求c;
(2)求的取值范围.
分析(1)根据三角形内角和定理和诱导公式,将三角形内角的三角函数关系转化为角的关系,求出其中的一个角,然后利用余弦定理列方程,即可求c的值.要注意角的范围和三角函数的单调性.
(2)利用(1)的结论B=,可得A+C=. 所以C=-A.
所以acosC ccosA=sinAcosiosAsinC=sin(2A-π),化成只含一个角的三角函数值,再利用三角函数的性质求出该式的范围.解析(1)由sin(A-B)=cosC,得sin(A-B)=sin(-C).因为ΔABC是锐角三角形,所以A-B=-C.即A-B+C=.
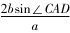
又A+B+C=π,所以B=.
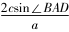
由余弦定理,得b2=c2+a2-2accosB 即(一道高考题的多解分析论文)2=c2+(3一道高考题的多解分析论文)2-2c·3一道高考题的多解分析论文cos. 即c2-6c+8=0,解得c=2或c=4.又当c=2时,b2+c2-a2=(一道高考题的多解分析论文)2+22
(3一道高考题的多解分析论文2)2=-4<0,所以b2+c2<a2,此时A为钝角,与已知矛盾,所以c≠2,故c=4.
(2)由(1)知B=,则A+C=,即C=-A.所以acosC ccosA=sinAcosiosAsinC==一道高考题的多解分析论文sin(2A-).2因为ΔABC是锐角三角形,所以<A<.所以-<2A-<.所以-<sin(2A-)<.所以-1<<1.故的取值范围为(-1,1).题2在ΔABC中,角A,B,C的对边分别为a,b,c,点D在边BC上,且sin∠BAD=2sin∠CAD.(1)若AD=b=2,cos∠BAD=,且∠CAD为锐角,求CD的长;(2)若BD=CD,求的值.分析(1)由题设可得sin∠BAD=,进而求得cos∠CAD=,应用余弦定理求CD的长;(2)由正弦定理可得sin∠CDA=,sin∠BDA=,结合∠CDA+∠BDA=180即可求目标式的值.
解析(1)由cos∠BAD=,0<∠BAD<π,则 sin∠BAD=.
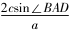
所以sin∠CAD==.
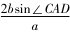
又∠CAD为锐角,则cos∠CAD=.又CA=AD=b=2,在ΔCAD中,cos∠CAD=
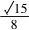
b2+b2-CD2==,可得CD=1.2b2
(2)由BD=CD=,在ΔCAD中,=,则sin∠CDA=.
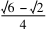
在ΔBAD中,=
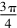
, 则sin∠BDA=
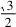
.又∠CDA+∠BDA=180°,故=.又sin∠BAD=2sin∠CAD,所以=2.
题3如图3,在平面四边形ABCD中,∠BCD=,AB=1,∠ABC=.
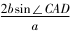
(1)当BC=一道高考题的多解分析论文,CD=一道高考题的多解分析论文时,求ΔACD的面积;(2)当∠ADC=,AD=2时,求cos∠ACD.分析(1)利用余弦定理求出AC,cos∠ACB,再利用诱导公式、三角形面积公式计算作答.
(2)在ΔABC和ΔACD中用正弦定理求出AC,再借助同角公式求解作答.解析(1)当BC=一道高考题的多解分析论文时,在ΔABC中,由余弦定理,得AC2=AB2+BC2-2AB·BCcos∠ABC.即AC2=3-2一道高考题的多解分析论文cos=5.解得AC=一道高考题的多解分析论文,则s 0.因为∠BCD=,又CD=一道高考题的多解分析论文,所以ΔACD的面积为SΔACD=AC·CDsin∠ACD=×一道高考题的多解分析论文×=.
(2)在ΔABC中,由正弦定理,得AB ACsin∠ACB=sin∠ABC.即AC==2cos一道高考题的多解分析论文ACD.在ΔACD中,由正弦定理,得AD Asin∠ACD=sin∠ADC.ADsinπ即AC=6=1 整理,得sin∠ACD=一道高考题的多解分析论文cos∠ACD.而sin2∠ACD+cos2∠ACD=1,∠ACD为锐角,所以cos∠ACD=一道高考题的多解分析论文/3.
参考文献:
[1]谢新华.一道2021年高三八省联考试题的多解探究[J].数理化解题研究,2022(07):95-97.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/70127.html
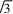 ,b=2
,b=2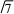 ,求ΔABC的面积;(2)若sinA+
,求ΔABC的面积;(2)若sinA+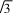 sinC=
sinC=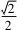 ,求C.2试题探析
,求C.2试题探析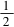 3 c·ccos150.所以7c2=28,解得c2=4.所以ΔABC的面积为S=acsinB=c2=
3 c·ccos150.所以7c2=28,解得c2=4.所以ΔABC的面积为S=acsinB=c2=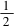 解法2由正弦定理可知a=
解法2由正弦定理可知a=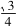 c⇔sinA=
c⇔sinA=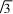 sinC.由B=150°,得A+C=30°所以03 sinC=sinA=sin(30°-C)=cosC-
sinC.由B=150°,得A+C=30°所以03 sinC=sinA=sin(30°-C)=cosC-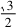 sinC.所以cosC=3sinC.由sin2 C+cos2 C=1,sinC>0,得sinC=1.
sinC.所以cosC=3sinC.由sin2 C+cos2 C=1,sinC>0,得sinC=1.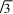 7由正弦定理知siC=siB.所以c=bs=2.从而a=2
7由正弦定理知siC=siB.所以c=bs=2.从而a=2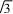 所以ΔABC的面积为S=acsinB=
所以ΔABC的面积为S=acsinB=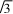
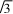 c·ccos150.所以7c2=28,解得c=2.从而a=2
c·ccos150.所以7c2=28,解得c=2.从而a=2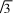 3.所以ΔABC的面积为S=
3.所以ΔABC的面积为S=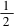 acsinB=
acsinB=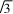

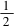 CD=c.
CD=c.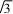
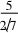 一道高考题的多解分析论文sinθ=5cosθ.结合sin2θ+cos2θ=1可得sinθ=
一道高考题的多解分析论文sinθ=5cosθ.结合sin2θ+cos2θ=1可得sinθ=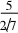 ,cosθ=.
,cosθ=.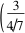 由AD+CD=AC=2一道高考题的多解分析论文,得一道高考题的多解分析论文csin(150°-θ)+csinθ=cosθ+sinθ)c=2一道高考题的多解分析论文.所以+)c=
由AD+CD=AC=2一道高考题的多解分析论文,得一道高考题的多解分析论文csin(150°-θ)+csinθ=cosθ+sinθ)c=2一道高考题的多解分析论文.所以+)c=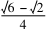 ,解得c=2.从而a=.
,解得c=2.从而a=.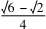 所以ΔABC的面积为S=acsinB=一道高考题的多解分析论文.
所以ΔABC的面积为S=acsinB=一道高考题的多解分析论文.
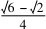 因为0°<C<30°,从而30°<C+30°<60°.所以C+30°=45°,解得C=15°.
因为0°<C<30°,从而30°<C+30°<60°.所以C+30°=45°,解得C=15°.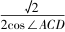 =cosC+sinC=.
=cosC+sinC=.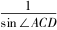
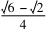 因为0°<C<30°,所以sinC=.
因为0°<C<30°,所以sinC=.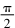 又因为sin15°=,所以C=15°.
又因为sin15°=,所以C=15°.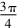 因为0°<C<30°,从而30°<60°-A<60°.所以60°-A=45°,解得A=15°.从而C=15°.
因为0°<C<30°,从而30°<60°-A<60°.所以60°-A=45°,解得A=15°.从而C=15°.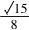 由余弦定理,得b2=a2+c2-2accos150°.所以()2=a2+c2+一道高考题的多解分析论文ac.
由余弦定理,得b2=a2+c2-2accos150°.所以()2=a2+c2+一道高考题的多解分析论文ac.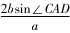 即a2=b2,故a=c,从而A=C.因为A+C=180°-B=30°,所以C=15°.
即a2=b2,故a=c,从而A=C.因为A+C=180°-B=30°,所以C=15°.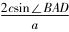 解法6因为sinB=,
解法6因为sinB=,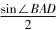 故sinA+一道高考题的多解分析论文sinC==一道高考题的多解分析论文sinB.由余弦定理,得b2=a2+c2-2accos150°.由正弦定理,得sin2 B=sin2A+sin2 C+一道高考题的多解分析论文3 sinA·sinC.故()2=sin2A+sin2 C+一道高考题的多解分析论文sinAsinC.所以sin2A=sin2 C.因为0°<A,C<30°,故sinA=sinC.从而A=C.因为A+C=180°-B=30°,所以C=15°
故sinA+一道高考题的多解分析论文sinC==一道高考题的多解分析论文sinB.由余弦定理,得b2=a2+c2-2accos150°.由正弦定理,得sin2 B=sin2A+sin2 C+一道高考题的多解分析论文3 sinA·sinC.故()2=sin2A+sin2 C+一道高考题的多解分析论文sinAsinC.所以sin2A=sin2 C.因为0°<A,C<30°,故sinA=sinC.从而A=C.因为A+C=180°-B=30°,所以C=15°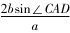 又A+B+C=π,所以B=.
又A+B+C=π,所以B=.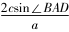

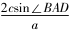 所以sin∠CAD==.
所以sin∠CAD==.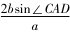 又∠CAD为锐角,则cos∠CAD=.又CA=AD=b=2,在ΔCAD中,cos∠CAD=
又∠CAD为锐角,则cos∠CAD=.又CA=AD=b=2,在ΔCAD中,cos∠CAD=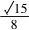 b2+b2-CD2==,可得CD=1.2b2
b2+b2-CD2==,可得CD=1.2b2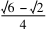 在ΔBAD中,=
在ΔBAD中,=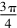 , 则sin∠BDA=
, 则sin∠BDA=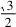 .又∠CDA+∠BDA=180°,故=.又sin∠BAD=2sin∠CAD,所以=2.
.又∠CDA+∠BDA=180°,故=.又sin∠BAD=2sin∠CAD,所以=2.