SCI论文(www.lunwensci.com):
摘 要 : 特殊值法可理解为对题目中未知量取具体的数值,代入有关代数式进行计算,从而实 现简便高效的解题.对此,本文着重探讨特殊值法在高中数学解题过程中的具体应用,帮助学生掌 握这种数学解题技巧,探寻数学解题新思路,能够举一反三、灵活变通地应对不同类型的数学题目.
关键词 : 高中数学; 特殊值法; 分类讨论
在解答某些数学题目的过程中,可以通过设题 中某个未知量为特殊值的方式帮助我们简化解题过 程,得到最终答案,这种解题策略的应用能够帮助学 生节省解题时间,提升解题效率.因此,从这个思路 出发,本文主要探讨特殊值法在数学解题中的具体 应用,并主要围绕转换角度、构造函数、代入检验、定 位变量以及合理赋值这几个方向展开具体探讨,以 帮助学生学会应用特殊值法高效简便解题,切实提 升数学解题能力.
1 转换角度,减少计算压力
特殊值法体现的是从一般到特殊,再从特殊到 一般的解题思想.如果数学题目中的已知条件十分 抽象、数量关系非常复杂、用常规思路解题难度很大 时,我们可以通过选择合适的特殊数、特殊点、特殊 数列、特殊图形等,转换问题思考的角度,从特殊中 探索解答问题的规律,正确求得答案.
例 1 如果 x、y、z 是全不相等的实数,且 a = x2 - yz,b = y2 -zx,c = z2 -xy,则下列结论正确的是 ( ) .
A.a,b,c 都不小于 0
.a,b,c 都大小于 0
C.a,b,c 至少有一个小于 0
D.a,b,c 至少有一个大于 0
解析 这道题中的未知数是比较多的,如果我 们用常规思路去解题的话,所构造出的代数式较为 复杂,解题难度较大.这时我们就可以应用特殊 值法的思路,根据题设条件由于 x,y,z 是不全相 等的实数,可取值的范围是比较大的,我们可 以 选择容易计算的实数如令 x = 1 ,y = -1 ,z = 1 ,分 别代入 a = x2 -yz,b = y2 -zx,c = z2 -xy 计算可得 a = 2 ,b = 0 ,c = 2 ,可排 除 B 和 C 选项 ; 继续取特 殊值令 x = 1 ,y = -1 ,z = 2 ,代入可得 a = 3 ,b = - 1 ,c = 5 ,可排除 A 选项,故正确答案为 D,快速 解答了该题目.
评析 在面对一些计算难度较大的数学题目的 时候,我们可以根据题设条件将其中的某个未知量 设为特殊值,但要注意这个量的取值要和最终要求 的结果有所联系,并且无论取值多少都不会影响最 后要求的量的值,这样才可以在一定程度上帮助我 们简化计算过程,减少计算压力,实现灵活高效解 题,从而提升数学解题的效率.
2 构造函数,避免分类讨论
构造函数的方法一般应用于函数、导数综合题 目的解答中.这类题目的难点就在于分类讨论和最 值转化,需要学生通过构造函数的方式来将复杂的 函数形式进行转化,这样才能往下推导计算,在实现 快捷解题的同时,更培养了学生融会贯通的能力.
例 2 设 a= [-1,1],且函数 g(x) = log22x + (a-4) log2 x + 4-2a 恒为正值,求 x 的取值范围.
解析 本道题目中给出的 g(x) 函数解析式是 关于 log2 x 的二次 函数,常规的解题思路是设 t = log2 x,则原函数转化为 u(t) = t2 + (a-4) t + 4-2a, 需进行较为复杂的分类讨论,学生们感到解题难度 非常的大,很多同学都选择了放弃.但我们再去观察 一下这道题目,参量 a 的范围题目中已经给出了,那 我们不妨利用主元变更法的思路来构造新的函数模 型,回避 分 类 讨 论.具 体 来 讲,学生可以把关于 log2 x 的二次函数转化为 以 a 为自变量的一次函 数,设f( a) = ( log2 x -2 ) a + log22x -4 log2 x + 4 , 那么要使f( a) 在设 a = [- 1 ,1]时恒大于零,我 们只需要取特殊点,当且仅当f( 1 ) >0 ,f( -1 ) > 0 时 即可成立,代入可得 log2 x < 1 或 log2 x >3 ,接 着解这两个不等式就可以得 出 x 的取值 范 围为 (0 ,2 ) ∪( 8 ,+ ∞ ) ,这样解题就高效简便 得 多 了,学生们也更容易接受.
评析 在实际解题中,教师要善于根据题目中 的条件,对题设条件中的不同情况加以分类,逐类求 解,这种分类讨论的方法是学生必须掌握的解答函 数类题目的基本思路,教师在教学中,要善于引导学 生捕捉题目中的关键信息,从而生成最佳的解题思 路,为高效解题奠定坚实的基础.
3 代入检验,获得信息矛盾
检验答案是教师应引导学生培养的一种良好学 习习惯.一方面,可以使学生通过检验判断答案是否 正确,当出现信息矛盾时及时纠错、改错,避免出现 粗心大意、考虑不全面等情况 ; 另一方面,有利于培 养学生思维的严谨性与深刻性,使学生形成良好的 学习品质与思维品质,提升学生的综合素养.
例 3 若数列{ an } 与{ bn } 中,a1 = b1 = 1,an + 1 - an = 2,bn /bn + 1 = 1/2 ( n ≥1 ) ,则{ an bn } 的前 n 项和
为( ) .
A.3 -(2n + 3) (1/2) 2 B.6 -(2n + 3) (1/2) 2 -
1
C.(3-2n) 22-3 D.(2n-3) 22 +
3
解析 首先我们可以取特殊值 n = 1,2,3,则 a1 、a2 、a3 依次为 1,3,5,同理 b1 ,b2 ,b3 依次为 1,2, 4,那么 a1 b1 = 1,a2 b2 = 6,a3 b3 = 20.接下来代入选项 进行检验,当 n = 1 时代入 A 选项,S1 = 3 - (2 + 3) / ( 1/2) 2 = -17 ≠1 = a1 b1 ,可排除 A 选项.同理代入 C 选项可得 S1 = (3-2) × 2 -3 = -1 ≠1 = a1 b1 ,可 排除 C 选项.最后将 n = 2 代入 B 选项,S2 = 6 - (2 × 2 + 3) ( 1/2) = 6-7/2 = 5/2 ≠1 + 6 = a1 b1 + a2 b2 , 可排除 B 选项,综合可得正确答案为 D.这样,通过 利用特殊值法和代入检验法,使该问题的顺利解答.
评析 一般来说,代入检验的基本思路是把最 终得到的答案带回原条件中进行检验,或者把答案 当作条件来解题目中的其他条件,以此来验证结果 是否正确.但有时因代入检验的计算量过大,会 浪费时间,学生也可以利用代入符合答案范围的 特殊值进行检验,通过特殊值、特例来快速检验 答案,提升检验 效率,这都是对学生灵活处理数 学问题能力的检验,也是学生深度理解和运用数 学知识的体现.
4 定位变量,加强数形结合
我们在对变量进行赋值或取特殊值的时候,如 果我们忽视题设的条件,没有充分考虑到变量的取 值范围,出现无效赋值或解题错误的情况,则无疑会 导致问题解决过程中出现南辕北辙,使得问题解决 功亏一篑.因此,对于某些数学题目来讲,学生要善 于运用数形结合的思想方法,借数的精确性与形的 直观性来使某些抽象的数学问题直观化、生动化,进 而可以有效定位变量的范围并进行赋值,找到解题 的切入点.
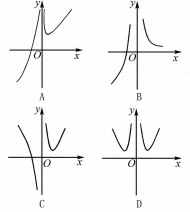
例 4 函数f ( x) = x + 1 / | x | 的 图 象 可 能 是 ( ) .
解析 在解答这类型题目的时候,我们可以结 合函数的单调性以及取特殊值的方法来进行判定.
以单调性来看,当 x=(0,1) 时,函数f(x) = x + 1/x, 为单调递减函数 ; 当 x=( 1,+ + ∞ ) 时,函数f(x) = x + 1/x,其图象为单调递增函数,当 x =( - ∞ , 0 ) 时,同理函数f(x) = x -1/x,为单调递增函数,可确 定正确答案为 A.除了这个方法之外,学生也可以取 一些特殊点,比如 x = -2,-1/2,1/2,1,2 等,代入 解析式结合图象来进行排除,这样能进一步缩短解 题时间.
评析 在利用特殊值法在解答这类型题目的时 候,我们对于变量的取值要符合题设条件与不同函 数定义域、值域等隐形条件,同时要善于抓好拐点、 极值点、最值点这些特殊点,充分理解这些特殊点的 含义,这样既能帮助我们利用赋值巧解复杂数学问 题,达到事半功倍的效果,更可培养学生面对数学问 题,能全面深刻的认知数学问题.
5 合理赋值,巧解不等式
特殊值法在解答不等式相关的问题中的妙用有 很多,甚至可以说是解答不等式类选择题目的首选 方法.我们可以通过对不等式中的变量赋予恰当的 数值或代数式,再加上恰当的运算和推理,就可以将 复杂的推导问题转化为简单的计算问题,进而通过 简化计算与推导过程帮助学生节省解题时间,达到 快速高效做题的目的.
例 5 设函数f(x) 在 R 上的导函数为f ' (x) , 且 2f ( x ) + xf ' ( x ) > x2 ,则在 R 上恒 成 立 的 是 ( ) .
A.f(x) >0 B.f(x) <
0
C.f(x) >x D.f(x) <x
解析 如果用常规思路去解题的话,根 据 2f(x) + xf ' (x) >x2 ,我们可以构造函数记 g (x) = x2f(x) ,令 g ' (x) = x[2f(x) + xf ' (x) ) ]= 0 得唯一 驻点 x = 0,那么当 x <0 时,g ' (x) <0,g(x) 单调递 减 ; 当 x >0 时,g ' (x) >0,g (x) 单调递增,也就是 g(0) 为该函数的最小值,g(0) = 0,因此恒有 g (x) = x2f(x) >g(0) = 0,可得f(x) >0,当 x = 0 时同样 满足,因此可得到正确答案为 A.但在解答这道题目 的时候,特殊值法是一个很好用的解题技巧,学生也 可以用这个方法来解题.不过这一次我们赋值的不 是特殊的数值,而是特殊的函数.我们可以根据已 知条件取容易计算的特殊函数f(x) = x2 ,则f ' (x) = 2x,那么题目中的 2f(x) + xf ' (x) 为 了 2x2 + x(2x) = 4x2 ,原不等式也就转化为 4x2 >x2 ,自然 而然是成立的.那么f(x) = x2 >0 对应 A 选项,可 得 A 选项是正确 的,这样对于解选择题来说就快 的多了.
评析 在数学解题中,教师根据题目条件,通过 结合具体的数学题目,使学生从中思考如何分析与 应用赋特殊值法,可以帮助学生有效掌握这种解题 策略,提升数学解题能力,让学生在灵活的数学解题 中树立对数学学习的信心.
总之,在解答数学题目的过程中,需要学生掌握 有关的数学知识、一定的解题技巧及解题思想.因 此,作为高中数学教师,我们要善于引导学生做好题 型的归纳与总结,学会从中提炼解题规律,掌握解题 技巧,进而能在遇到同类型题目时,从脑中的知识体 系和解题技巧体系中逐一搜索,找到适合的解题思 路与方法,这样才能真正提升数学解题能力,培养良 好的数学素养.
参考文献 :
[1]刘海杰.构造法在高中数学解题中的运用措施 分析[J].数理化解题研究,2022 (12) : 14 -16 .
[2]许佳,陈振锋.例析特值法在数学解题教学中的
应用[J].中学数学研究,2021 (3) : 54-55 .
[3]褚梦琪.运用特殊值法,提升高中数学的解题效 率[J].语数外学习,2017 (1) : 35-35 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69037.html