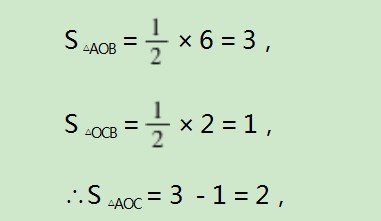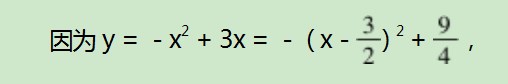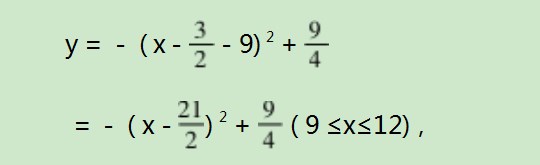SCI论文(www.lunwensci.com)
摘要:将模型思想融入初中数学教学中,有助于深化学生对数学知识本质的理解,掌握运用数学知识解决问题的思路与方法,促进其学习能力的进一步提升.教学实践中应结合学生的认知规律以及具体教学内容,采取针对性的融入策略,使学生牢固掌握相关的数学模型,并灵活应用于解题中.
关键词:初中数学;模型思想;融入;教学
模型思想是一种运用数学模型解决问题的思想.在该思想指引下可进一步提升学生的学习效率,迅速找到解决问题的思路.初中数学教学中应为学生剖析相关的理论知识,做好数学模型的归纳,尤其要展示模型思想在解题中的具体应用,以进一步提高学生的灵活应用能力.
1剖析模型理论
初中数学涉及有很多的模型,如一次函数模型、二次函数模型、反比例函数模型等.教学中应通过列举实例为学生讲解数学模型的本质,运用数学模型解决问题的思路与方法以及应用注意事项.同时为增强学生运用模型思想解题的自信心,应注重为学生创设熟悉的问题情境,进一步夯实学生所学的理论知识.
例如在讲解二次函数模型时,为学生展示如下问题情境:某药店新进一批消毒液,每瓶的进价为10元,在销售中发现销售量y(瓶)和每瓶售价x(元)存在一次函数关系(其中10≤x≤21且x为整数),当售价定为12元时,每天销售量为90瓶;当售价定为15元时,每天销售量为75瓶.若每天的销售利润为w元,则售价定为多少元时,每天获得的利润最大?
解答该题应先构建销售量y和售价x的函数模型,而后构建每天利润和售价的函数模型.
根据题意可知y=kx+b,根据已知条件不难求出k=-5,b=150,y=-5x+150,则w=(x-10)(-5x+150)=-5x2+200x-1500(10≤x≤21且x为整数),由二次函数性质可得x=-=20时,w取得最大值500,即每瓶的售价为20元时,每天可获得最大利润500元.
2讲解相关例题
初中数学课本中的最短路径问题,实际上属于“将军饮马模型”.讲解该模型时应注重给学生预留空白的时间,要求学生认真揣摩求解最短路径的思路,使其能够真正地顿悟、理解与掌握.同时,为更好地锻炼学生的学以致用能力,在完成该模型的讲解后,应为学生讲解经典的例题,进一步拓展其视野,使其更好地把握“将军饮马模型”的本质,在以后的解题中能够以不变应万变.例如,可在课堂上为学生讲解如下例题:
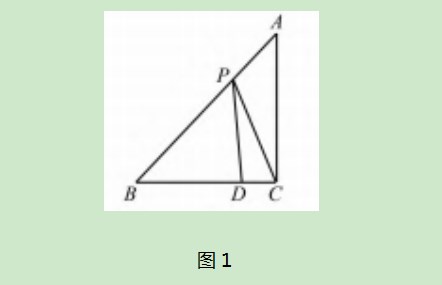
如图1,△ABC为等腰直角三角形,其中∠ACB=90°,AC=BC,点D为BC上一点,BD=6,DC=2,点P为AB上一动点,则PC+PD的最小值为().
A.8 B.10 C.12 D.14
从“将军饮马”模型中获得解题启发.
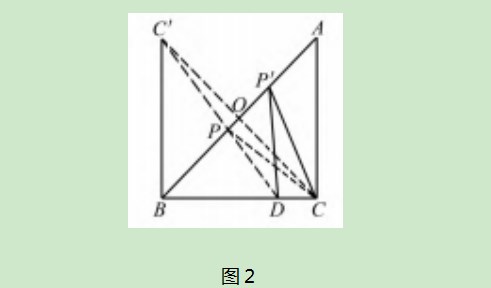
如图2,过点C作CO⊥AB,垂足为点O,延长CO到C',使得OC'=OC,连接DC'交AB于点P,连接CP.易知CP=C'P,所以PC+PD=C'P+PD,显然当C'、P、D三点处在同一条直线上时其和最小.连接BC',则由对称性可知∠C'BA=∠CBA=45°,所以∠CBC'=90°,则BC'⊥BC,∠BCC'=∠BC'C=45°,BC=BC'=8,由勾股定理可得DC'=^BC'2+BD2=10,选择B项.
3加强专题训练
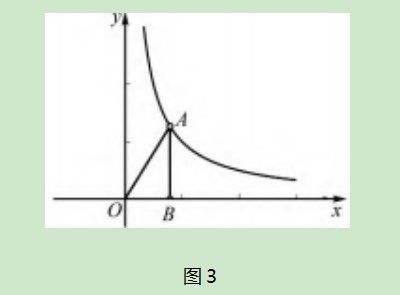
初中数学教学中为使学生更好地掌握建模思想的应用技巧,应结合学生的具体情况,以及数学模型的重要程度,积极组织学生加强相关的专题训练活动.通过训练使学生不断地犯错、纠错,加深对数学模型的认识与理解,提高运用模型思想解题的效率.如在讲解反比例函数知识时,引导学生关注如下模型:如图3所示,在y=k/x图像上存在一点A,过点A作AB⊥x轴,垂足为点B,则S△AOB=2.该模型是初中数学各类测试以及中考的参考模型,教学中可引导学生自行推导该模型的结论,与此同时向学生展示如下习题,及时对学生进行训练,使学生能够当堂掌握该模型:
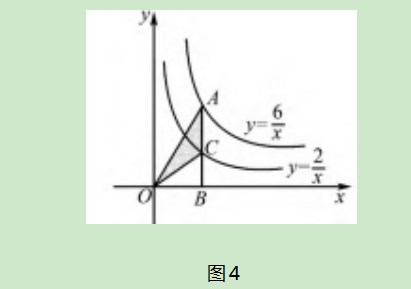
如图4,点A为反比例函数y=6/x的图象上一点,过点A作AB⊥x轴,垂足为B,线段AB和反比例函数y=2/x的图象交于点C,则△AOB的面积为().
A.4 B.3 C.2 D.1
习题属于在模型的基础上有所延伸,能很好地考查学生对模型的理解程度.
实际上,S△AOC=S△AOB-S△OCB,
由模型中的结论可很快地计算出
选择C项.
4重视学习总结
初中数学教学中为使模型思想更好地融入到教学中,应注重引导学生学会学习,鼓励学生做好学习的总结与反思.如对常见问题的提炼与抽象,自行推导相关数学模型,并在解题中加以应用.同时,能够主动与其他学生交流学习心得,学习他人总结出的数学模型,更好地提高自身的解题能力.二次函数图象的平移是初中数学的重要知识点.教学中应引导学生进行总结,推导出相关的模型,指引其以后更好地解题.
在教师的指引下,学生总结出了如下模型:
对于二次函数y=ax2+bx+c(a≠0),先转化为顶点式y=a(x+h)2+k,其图像沿x轴平移m个单位,沿y轴平移n个单位得到的函数解析式为y=a(x+h+m)2+k+n,其中沿x轴分别向左、向右平移时,m分别取正、负;沿y轴分别向上、向下平移时n分别取正、负,简称“左加右减,上加下减”.另外,点的平移也遵循该规律.为使学生体会到应用该模型解题的便利,可要求学生应用推导的模型解答如下习题:
将一段抛物线y=-x2+3x(0≤x≤3)向右平移9个单位,得到的新抛物线和直线y=x+b有唯一公共点,则b的取值范围是.
由平移模型可知新得到的函数解析式为
将其和直线y=x+b联立,消元得x2-20x+108+b=0
令Δ=0,得到b=-8.
同时,观察平移后的图像可求得b的取值范围为-12≤b<-9.
综上,b的取值范围为b=-8或-12≤b<-9.
模型思想是一种重要的分析问题的思想,在初中数学中占有重要地位.实践中为使学生更好地掌握模型思想,能够具体问题具体分析,提高其应用模型思想解题的灵活性,掌握运用模型思想的解题技巧,可按照理论剖析、例题讲解、习题训练、学习总结这一思路开展教学工作,实现模型思想与初中数学教学活动的有效融合.
参考文献:
[1]欧琼华.初中数学教学中融入模型思想的策略[J].名师在线,2021(18):66-67.
[2]黄屹东.融入模型思想优化初中数学教学[J].新智慧,2021(01):91-92.
[3]龚华敏.论数学模型思想在初中数学教学中的渗透[J].数理化解题研究,2021(11):30-31.
[4]莫宇平.应用模型思想提高学生数学应用能力探研[J].成才之路,2021(11):58-59.
[5]邱宗如.初中数学模型思想的教学实践与思考[J].福建中学数学,2020(08):43-45.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/63942.html