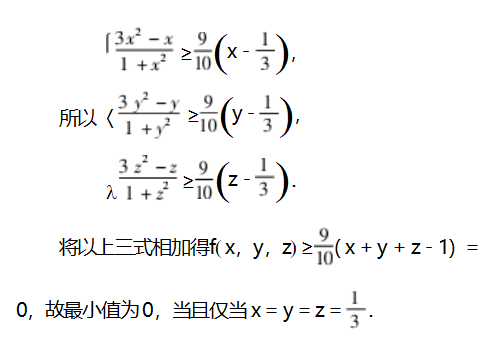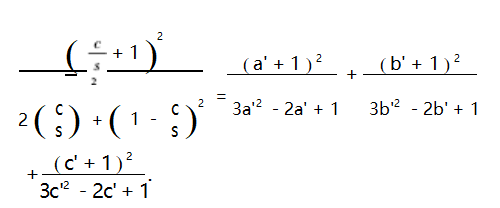SCI论文(www.lunwensci.com)
摘要:本文以函数与导数为主要工具,主要应用“切线放缩”与“割线放缩”证明代数不等式,突出数形结合思想中的“以直代曲”思想.本文突出呈现函数“凸性”在此方法中的重要性,并把它作为选择具体直线时的思路切入点.
关键词:代数不等式,证明,以直代曲,函数的凸性
我们经常会见到一类条件不等式,给出有限个变量的范围或它们和的值,之后证明与这些变量有关的代数式的和的取值范围.
一种通常的表现形式是:
当然,等号或不等号的呈现形式也不唯一,以上仅作为一个常见表示展现给大家,目的是从形式上先做了解.我们可以看到,很多解答中对这类问题都展现了非常高超的配凑变形技巧,这让我们不禁思考:对于这类问题在思考时的总体方向是什么?本文就将深入探究这类问题,将思考的过程予以展现,找出问题思考的总体方向,寻找隐藏在变形技巧后面的总体规律,并形成主要的解题思想——以直代曲.
1“以直代曲”思想之割线放缩技巧
割线放缩是以直代曲思想的重要呈现,它的理论基础是函数的凸性.关于函数的凸性,我们利用二阶导数判断,当f″(x)≤0在区间M上成立时,f(x)在区间M上为上凸函数;当f″(x)≥0在区间M上成立时,f(x)在区间M上为下凸函数.
点评本题是利用割线放缩的一道典型例题,首先,整体的放缩方向是“往大放”,同时考虑到函数的凸性是“下凸”,于是想到“封口”处理.从图1来看,直线和函数是“割线”关系,故名割线放缩.事实上,根据刚才对例题的分析可以看到,函数的凸性是在放缩过程中必须要重点考虑的一个部分.可以看到,割线放缩的关键是根据不等式的结构形式,找到要研究的函数,之后研究这个函数的凸性区间端点等非常重要的信息,之后确定直线的位置.
2“以直代曲”思想之切线放缩技巧
通过刚才的分析,我们知道分析函数的凸性是极为重要的,这点不仅仅是应用在割线放缩中,切线放缩也至关重要.同样,切线放缩也是“以直代曲”思想的重要呈现.
事实上,我们分别将0和1代入二阶导数,发现符号相反,这说明在区间[0,1]上,函数的凸性发生了改变.即使凸性不一致也没关系,我们看看本题可能会用到的取等条件.我们猜测是x=y=z=1计算在此处g(x)的二阶导数大于0,说明此处函数下凸.根据不等式的方向是“往小放”,所以我们使用切线放缩.
本题依据函数在取等条件时的凸性决定使用切线放缩.本题的函数凸性不唯一,所以在证明时我们用了作差比较来严格证明.例1的函数凸性唯一,所以我们使用图象说明即可.切线放缩是一种更为常用的与函数凸性结合的方法,一般的步骤仍然是先分析函数凸性,根据不等号方向确定切线放缩的直线,同时,切点可以根据取等条件确定.
所以,令a+b+c=1,得到的是等价不等式,这样处理是合理的.
3“以直代曲”思想之切割线放缩的综合应用
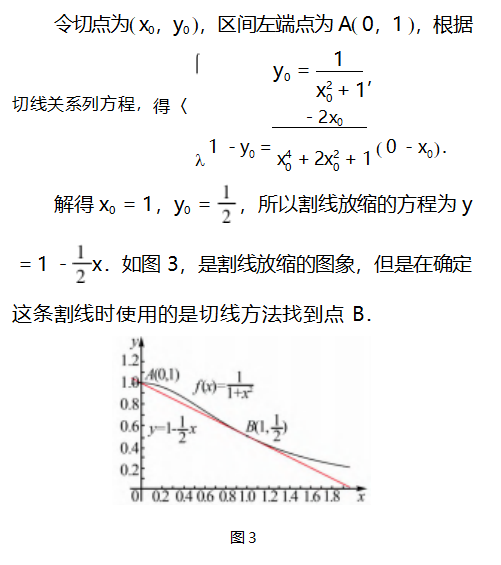
可以看出,在[0,2]上函数凹凸性不唯一,应该是先上凸再下凸.结合要放缩的方向,我们总体上使用割线放缩.但是,因为是先上凸后下凸,如果连接区间端点的话就会穿过图象,我们的考虑是从区间左端点向下凸部分引切线.也就是说,我们用“切点”作为割线放缩“封口”的另一个端点.
从本题来看,虽然主体使用了割线放缩,但是其中的一个端点使用了切点,也就是说,本题综合使用了前面的两个“以直代曲”的思路.事实上,在具体利用直线放缩不等式的时候,不是固定用切线或者是割线,而是一定要根据函数的凸性,“因地制宜”地选择解决问题的方法.
本文展示了“以直代曲”的具体思想来解决代数不等式问题,给出了每一个放缩时具体用的函数图象.在实际做题中,函数的凸性分析是至关重要的.一定要在具体的问题中灵活运用,用图形从直观形象的分析中尽快找到解决问题的思路.
参考文献:
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[M].北京:人民教育出版社,2020.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/60979.html