SCI论文(www.lunwensci.com):
摘要:线性代数课中讲到矩阵的行阶梯形不唯一,但其最简形是唯一的,然而课本上并未给出证明。本文利用矩阵初等行变换知识结合向量的线性相关知识,给出矩阵行最简形唯一性的一个初等证明。
关键词:初等行变换;行阶梯形;行最简形;线性相关
本文引用格式:金永,等.行最简形唯一性的初等证明[J].教育现代化,2019,6(30):158-159.
在给工科学生讲授线性代数课,讲到矩阵的初等变换、行阶梯形、行最简形时,我们会提到行阶梯形是不唯一的,而行最简形是唯一的,学生在此处总会追问为什么行最简形是唯一的?它的唯一性课本《工程数学线性代数》[1,2]上并没有给出解释,一些其他线性代数课本如《经济管理数学基础线性代数》[3]或经典的《高等代数》[4]上又不涉及这一概念,然而我们知道行最简形对于求解线性方程组也是很关键的(尤其学生进行手算时)。基于上述原因本文尝试给出一种初等的证明,使学生在掌握初等行变换以及向量线性相关性知识的前提下可以自行解除对这一问题的疑惑。
设矩阵Am×n在进行初等行变换过程中出现的两个任意状态为M1和M2(可以认为M1和M2是两个不同同学对矩阵A进行初等行变换过程中出现的两个矩阵)。注意M1和M2的任意性。
引理1。M1和M2是行等价的。证明:显然存在m阶可逆矩阵P1和P2使得P1A=M1,P2A=M2。所以A=P1-1M1=P2-1M2。可得P2P1-1M1=M2。即M1与M2行等价。将M1和M2按列分块,设M1=(α1,α2,…,αn),
M2=(β1,β2,…,βn)。
引理2。向量组α1,α2,…,αn与β1,β2,…,βn有完全一致的线性关系。证明:由引理1知存在m阶可逆矩阵P使得PM1=M2。从线性方程组的角度来看,这说明由M1到M2进行的是保持解的消元变换[5],即,对任意的j,αj能表示成其余向量的表示形式同βj能表示成其余向量的表示形式是一致的(因为这是保持解的变换)。这就说明了向量组α1,α2,…,αn与β1,β2,…,βn有完全一致的线性关系。
引理3。设αj,βj如前所述,则对于1≤j≤n,αj=0当且仅当βj=0。此处0表示零向量(以下同)。证明:由引理1知存在m阶可逆矩阵P使得PM1=M2。即P(α1,α2,…,αn)=(β1,β2,…,βn),所以Pαj=βj,1≤j≤n再由,P的可逆性知αj=0当且仅当βj=0。显然要证明行最简形的唯一性只需证明由M1和M2化成的行最简形相等。以下我们约定,以αj(或βj)的第i个非零元素出发进行消元变换,指的是,以矩阵M1(或M2)的(i,j)位置元素为目标,最终将该位置元素化为1,该列其余位置都为0的初等行变换。
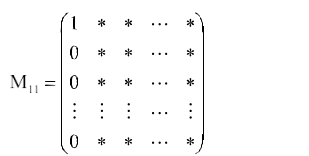
定理M1和M2化成的行最简形相等。证明:首先不妨假设α1≠0,由引理3知β1≠0。以α1的任意非零分量出发进行消元变换,再交换行(如果有必要交换的话),则M1可化成如下形式:
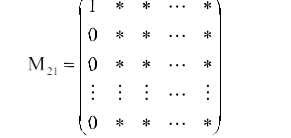
同理,以β1的任意非零分量出发进行消元变换,再交换行(如果有必要交换的话),则M2可化成如下形式:
变换之后的矩阵M11和M21按列分块后仍记为向量组α1,α2,…,αn和向量组β1,β2,…,βn(以下同)可知α1=β1。注意此时引理1、引理2、引理3仍成立。以下对α2进行讨论:α2=0;由引理3知β2=0。
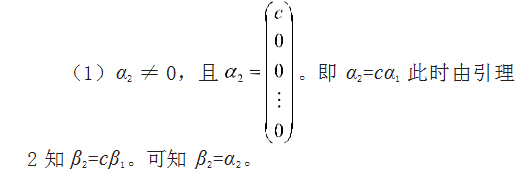
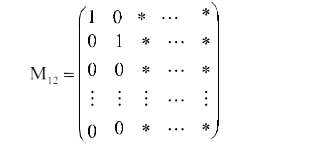
(2)α2≠0,且α2从2个分量开始至少有一个非零分量。由引理2知β2从2个分量开始至少有一个非零分量。以α2的第二个分量(包含第二个)之后的任意非零分量出发进行消元变换,再交换行(如果有必要交换的话),则M11可化成如下形式:
同样,以β2的第二个分量(包含第二个)之后的任意非零分量出发进行消元变换,再交换行(如果有必要交换的话),则M21可化成如下形式:
综上可知要么 β2=α2,要么经过初等行变换可化

后面再用类似的方式逐个讨论α3,α4,…。n步之后,必有α1=β1,α2=β2,…αn=βn。即M1n=M2n。说明M1与M2有相同的行最简形。推论:矩阵A的行最简形唯一。
参考文献
[1]工程数学线性代数第五版.同济大学数学系编.高等教育出版社.
[2]工程数学线性代数第六版.同济大学数学系编.高等教育出版社.
[3]经济管理数学基础线性代数.陈殿友术洪亮主编.清华大学出版社.
[4]高等代数第二版.北京大学数学系几何与代数教研室代数小组编.高等教育出版社.
[5]高等代数第三版.北京大学数学系几何与代数教研室前代数小组编王鄂芳石生明修订.高等教育出版社.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/9749.html