SCI论文(www.lunwensci.com):
摘 要 :本文从矩阵的初等行变换出发,分别提出在矩阵、向量组、线性方程组、矩阵的特征向 量、二次型中的一些应用,并呈现对应例题,加强学生对矩阵的初等行变换的理解与应用.
关键词 :初等行变换;矩阵;向量组;线性方程组
目前,《线性代数》这门课程是理工科和经管类 必开设的一 门课程,主要内容包括行列式、矩阵、线 性方程组、向量组、相似矩阵、二次型等. 矩阵的初等 行变换贯穿在整个线性代数的内容中,为了方便学 生学习,下面归纳总结了关于矩阵初等行变换在线 性代数中的应用.
1 矩阵中的应用
1. 1 求矩阵的逆
若矩阵 A 可逆,则 A - 1 也可逆,A - 1 可以表示成 若干个初等矩阵的乘积,因此可由矩阵的初等行变 换求 A - 1,即(A,E) 初等行变(E,A - 1 ),我们将矩 阵 A 和单位矩阵 E 都做初等行变换,当矩阵 A 化为 单位矩阵 E 时,单位矩阵 E 就变成了 A - 1 .
1. 2 求矩阵的秩
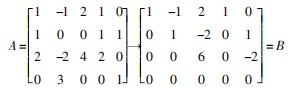
矩阵秩的定义是非零子式的最高阶数,我们知 道初等变换不改变矩阵的秩,对矩阵 A 做初等行变 换化为行阶梯形矩阵 B,由行列式的性质可知,矩阵 A 和矩阵 B 的非零子式最高阶数相同,所以矩阵 A 与矩阵 B 的秩相等.
因为矩阵 B 中有三个非零行,即 R ( B ) =3,所 以 R (A ) =3.
2 在向量组中应用
2. 1 求向量组的秩
由于任何矩阵 A,它的行秩 =列秩 =R (A ),因 此我们只需将向量组中的向量均按列构成一个矩阵 A,向量组的秩就等于矩阵 A 的秩.
例 3 求向量组 α 1 = ( 1,- 2,2 ),α2 = ( 1,- 4, 0 ),α3 = ( 1,- 2,2)的秩.
解 以
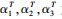
为列向量构成矩阵 A,并对矩 阵 A 进行初等行变换,把 A 化为阶梯形矩阵 B.
R (A ) =R ( B ) =2,又因为向量组 α 1,α2,α3 的秩等 于矩阵 A 的秩,即向量组 α 1,α2,α3 的秩为 2.
2. 2 求向量组的极大无关组
由于初等行变换不改变矩阵列向量的线性关系, 因此可由初等行变换求解向量组的极大无关组.
例 4 求向量组 α 1 = ( 1,2,3,0 ),α2 = ( - 1,- 2,0,3 ),α3 = (2,4,6,0 ),α4 = ( 1,- 2,- 1,0 ) 的 一个极大线性无关组.
解 以
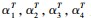
为 列 向 量 构 成 矩 阵 A, 并对矩阵 A 进行初等行变换,把 A 化为行最简形 矩阵 B.
非零行首非零元 1 所在的列作极大线性无关 组,因此向量组 α 1,α2,α3,α4 的一个极大线性无关 组为 α 1,α2,α4 .
3 在线性方程组中的应用
通过一系列的初等行变换,将系数矩阵或增广矩阵化为行最简形矩阵,判断方程组是否有解,有解 的情况下,求出通解.
3. 1 解齐次线性方程组
例 5 求解齐次线性方程组
3. 2 解非齐次线性方程组
例 6 求 非 齐 次 线 性 方 程 组
解 对增广矩阵 B 进行初等行变换,化为行最 简形矩阵.
可以得出系数矩阵的秩等于增广矩阵的秩,并 且小于未知量的个数,因此方程组有无数个解. 即它
的同解方程组为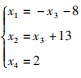 其中 x3 为自由未知量,令自由未知量 x3 =0,得特解
其中 x3 为自由未知量,令自由未知量 x3 =0,得特解 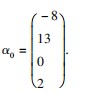
导出组的同解方程组为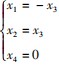 ,其中 x3 为自由未知量,令 x3 = 1,得对应齐次线性方程组的基础解系
,其中 x3 为自由未知量,令 x3 = 1,得对应齐次线性方程组的基础解系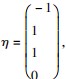 所以线性方程组的通解为 α0 + cη
所以线性方程组的通解为 α0 + cη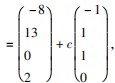 ,其中 c 为任意常数.
,其中 c 为任意常数.
4 在矩阵特征向量中的应用
上面我们介绍了用初等行变换求解线性方程 组,计算矩阵的特征向量就会涉及到解齐次线性方程组.
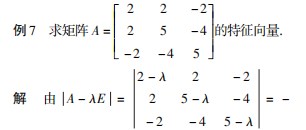 ( 1 - λ )2 ( λ - 10 ) =0,得矩阵的特征值 λ 1 = 10,λ2 =λ3 =1.
( 1 - λ )2 ( λ - 10 ) =0,得矩阵的特征值 λ 1 = 10,λ2 =λ3 =1.
矩阵的初等行变换贯穿于整个线性代数章节 中,熟练应用初等行变换是学好线性代数的基础,学 生要在平时学习中,学会归纳总结,使每个知识点建 立联系.
参考文献 :
[ 1 ] 同济大学数学系. 工程数学线性代数[ M ] . 北京 : 高等教育出版社,2014 .
[2 ] 郝秀梅,姜庆华. 线性代数[ M ] . 北京 :经济科学 出版社,2017 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/43670.html



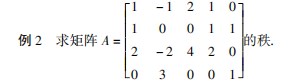
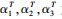 为列向量构成矩阵 A,并对矩 阵 A 进行初等行变换,把 A 化为阶梯形矩阵 B.
为列向量构成矩阵 A,并对矩 阵 A 进行初等行变换,把 A 化为阶梯形矩阵 B.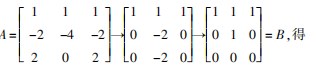
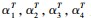 为 列 向 量 构 成 矩 阵 A, 并对矩阵 A 进行初等行变换,把 A 化为行最简形 矩阵 B.
为 列 向 量 构 成 矩 阵 A, 并对矩阵 A 进行初等行变换,把 A 化为行最简形 矩阵 B.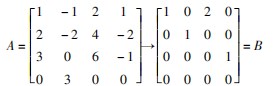

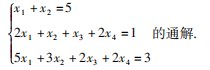
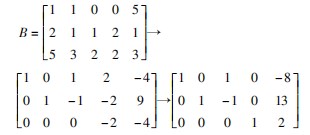
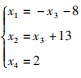 其中 x3 为自由未知量,令自由未知量 x3 =0,得特解
其中 x3 为自由未知量,令自由未知量 x3 =0,得特解 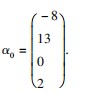
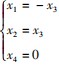 ,其中 x3 为自由未知量,令 x3 = 1,得对应齐次线性方程组的基础解系
,其中 x3 为自由未知量,令 x3 = 1,得对应齐次线性方程组的基础解系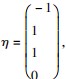 所以线性方程组的通解为 α0 + cη
所以线性方程组的通解为 α0 + cη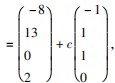 ,其中 c 为任意常数.
,其中 c 为任意常数.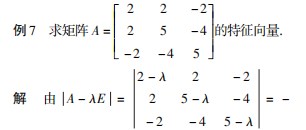 ( 1 - λ )2 ( λ - 10 ) =0,得矩阵的特征值 λ 1 = 10,λ2 =λ3 =1.
( 1 - λ )2 ( λ - 10 ) =0,得矩阵的特征值 λ 1 = 10,λ2 =λ3 =1.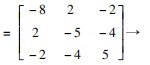
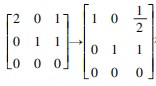 得基础解系
得基础解系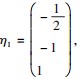 故 A 的对应于特征值 λ 1 =10 的全部特征向量为 c1
故 A 的对应于特征值 λ 1 =10 的全部特征向量为 c1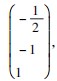 其中 c1 为任意非零常数.
其中 c1 为任意非零常数.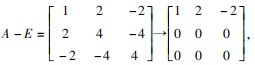
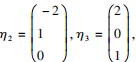 故A的对应于 特 征 值 λ2 = λ3 =1 的全部特征向量为
故A的对应于 特 征 值 λ2 = λ3 =1 的全部特征向量为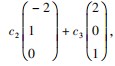 其 中 c2 , c3 是 不 全 为 零 的 任 意常数.
其 中 c2 , c3 是 不 全 为 零 的 任 意常数.