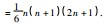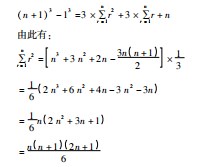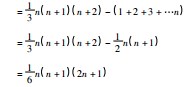SCI论文（www.lunwensci.com）:
1二次幂求和公式的产生
早在公元前300多年的古巴比伦数学文献中就有对…次幂求和的探索,并得出1
2+2
2+3
2
的结果.此后人们进一步求出了一般的…次幂求和公式,得出
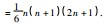
这个公式是如何推导出来的,后人从不同的角度对此做了许多猜想和验证,不仅方法多样,还直观易懂,其中蕴含的数学思想方法启迪后来者继续对这个问题进行探索.本文根据人的思维发展特点和心理发展规律,提出归纳法是最接近古人思维的一种方法,即与一次幂求和公式进行对比,找到规律,推导过程如下:
1２ ：１ ＝１
但这只是对古巴比伦人做法的一种猜测.
历史上…次幂求和公式的推导基本是沿着代数和几何两条脉络进行的.古希腊人用几何图形求解代数问题的思想给…次幂求和公式的几何代数法提供了启示.如毕达哥拉斯学派对三角形数的研究可以非常直观的求出自然数列的求和公式,只需将两个完全相同的三角形数拼成一个n行n+1列的平行四边形,由此一个n层的三角垛中所包含的点数就是n(n2+1),这种方法相比高中等差数列求和的倒序相加法更容易理解和记忆.同样地,对正方形数的研究也会对…次幂求和问题有一定的启示意义.阿拉伯数学家奥马·海亚姆就通过几何代数的方法进行了推导,…次幂求和就是图中所有正方形的体积之和,可转化为大长方形面积减去各个小长方形面积之和.这种方法更具有一般性,不仅可以求…次幂和,还可解决更高次幂求和问题.
数学进入近代以后,人们转而从代数角度运用公式进行演算,如17世纪法国数学家帕斯卡对次数为3的…项式进行变形,利用裂项相消的方法把三次幂进行降幂处理,推出了…次幂求和公式,其方法如下:
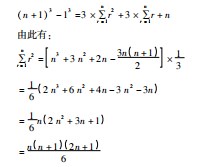2两种尝试
在初等数学中,对于项数较多的数列求和计算题用裂项相消法可以极大地简化计算.本文在前人成果的基础上,作了如下两种尝试.方法1:裂项相消法…次幂的一般形式为n2,我们对n2作如下变形:
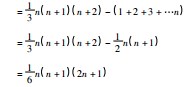
此法沿用了裂项相消的思想,把…次幂求和转化为自然数列求和,从而达到简化计算的目的.
方法2:公式法
本文在帕斯卡的基础上进行了改进,运用立方差公式推导出了…次幂求和公式.
3一点感想
在数学发展的过程中,对某一问题的研究,不同的人往往会从不同的角度进行思考,因此会有不同的创新点.也正因为如此一题多解在发展思维方面有独特的作用.通过数学史,我们可以了解古人的思维方法,发现古人思维的闪光点.而古今方法的对比,往往可以给我们很多思维上的启迪.把数学史融入数学教学作为数学教育领域中的一个课题,对今天数学教育的改革有积极的意义.教学中我们可以针对某一知识点向学生展示古人解决问题的方法,引导学生学习古人追求真理的精神,把我们的数学课题变成一门有血有肉活生生的课堂,更好地激发学生学习数学的兴趣.
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/51153.html
