SCI论文(www.lunwensci.com):
摘要:构造函数法是具有转化性质的数学思想,在高中数学解题中应用广泛,通过运用该方法将抽象、复杂的数学知识简化,变成学生能解决的问题形式,从而提高解题效率。文章介绍构造函数法的内涵,就该方法在数列题、不等式、方程等题型中的应用进行介绍,希望能抛砖引玉,与高中数学教师共同交流和进步。
关键词:高中数学,解题教学,构造函数法
构造函数法对学生综合能力要求较高,学生不但要扎实掌握基础知识,也要灵活应用知识。但在教学实践中,笔者发现很多学生不懂得如何构造函数,解题逻辑不清晰,走了不少弯路,对此应结合教学内容和学生接受能力,对构造函数法在各类题目中的应用进行详细解释,重点要求学生多看、多想、多练,做到陶行知先生所说的“让学生走上创造之路,手脑并用,劳力上劳心”。
一、构造函数法
构造函数法是指运用函数概念和性质,构造辅助函数来解题的方法,其关键在于找到反映题目特征的函数,再利用函数的性质解决问题。构造函数法是一种具有较强灵活性、创造性的解题模式,其应用必须符合以下几个原则:(1)构造的函数必须能与原题形成有效的联系;(2)构造出的函数在求解时必须比原有解题方法的难度小;(3)构造出的函数在单调性、奇偶性、周期性等方面应和原题目相符,以杜绝函数错误的问题。此外,在构造函数的过程中还应分析命题的条件、结论等,厘清其逻辑,再根据题目条件排列组合,最终得出构造函数。
二、构造函数法在高中数学解题中的应用
构造函数法在很多题型的解答中都有很大用处,以下就常用的题目类型进行介绍。
1.在数列题中的应用
数列是高中数学的重难点,包括等比、等差数列等,数列知识常与其他数学知识综合命题,解题难度大。对于此类综合型题目的求解,教师一方面要引导学生熟练掌握各类数列的概念、通项公式的解法,夯实数列知识基础;另一方面要选择有代表性的题目让学生练练手,在解题过程中总结技巧,积累经验。
例题1已知{an}为等比数列,且a1=2,a8=4,函数f(x)=x(x-a1)(x-a1)(x-a1)...(x-a1)。求f′(0)的值。
这道题目是函数和数列的综合题,解题关键在于仔细分析函数表达式和求解内容,采用构造函数法列式:f(x)=xg(x),再利用数列性质求解。
令g(x)=(x-a 1)(x-a2)(x-a3)…(x-a8),因此f(x)=xg(x),求导后得出f′(x)=g(x)+xg′(x)。可知,f′(0)=g(0)=a1·a2·a3…·a8,因a1=2,a8=4,可知g(0)=a1·a2·a3…·a8=(2×4)4=212。
2.在不等式中的应用
不等式是高中数学的重要知识点,从高考命题来看,命题组对不等式相关问题的考查力度越来越大,题型包括不等式问题变形、抽象函数不等式求证等,在这类题目的解答中,主要是利用构造函数进行求导,得出答案。
以不等式证明类题目的解答为例,这类题目的解答中,若直接从题目已知条件进行证明分析,难度很大,甚至无法证明,对此必须进行不等式分析,根据不等式结构形式构造函数,再利用函数的单调性证明。

在这道题目的解答中,通过观察不等式的结构不难发现这三个分式的结构很类似,引入函数构造法后,可以构造函数f(x)=,再利用函数的单调性证明不等式,如下所示。
证明:根据已知条件构造函数f(x)=

,可
知函数f(x)在(-∞,-1)和(-1,+∞)递增。因不等式性质|a+b|≤|a|+|b|,因此
 在这类题目的证明中,教师应引导学生仔细观察题目,灵活使用构造函数法,再利用函数性质快速得出答案。
在这类题目的证明中,教师应引导学生仔细观察题目,灵活使用构造函数法,再利用函数性质快速得出答案。
3.在方程中的应用
对高中生而言,方程并不陌生,他们从初中就接触方程,但高中阶段的方程题型更加多样,求解更加复杂,解答难度骤增。对于一些非常复杂、难以直接求解的方程题,可以利用构造函数法对问题进行转化,降低解答难度,再得出答案。
例题3解方程3x+4x+5x=6x
这道题目的方程既不能合并,又不能分解,直接求解难度很大,在解题时,可以根据方程和函数的关系来巧妙构造函数,再借助函数解方程。
4.在解析几何中的应用
解析几何是高考必考点,题目难度不一,充分挖掘题干中的各种条件,综合运用多种解题方法才能得出答案。教师在教学中应灵活运用多重方法帮助学生理解和记忆各种计算公式,通过绘制思维导图等方法加深知识印象,形成知识网络。同时,教师也要选择合适的题型引导学生掌握多样化的求解方法,增强学生的解题自信。
例题4已知实数a、b、c、d满足

=

=1。已知e是自然对数的底数,求(a-c)2+(b-d)2的最小值。
在这道题目的解答中,教师应引导学生仔细观察题目中的等式,再构造函数。
解:因
 =1,所以b=a-2ea,构造函数f(x)=x-2ex,点(a,b)在函数图像上。同理,因
=1,所以b=a-2ea,构造函数f(x)=x-2ex,点(a,b)在函数图像上。同理,因 =1,所以d=2-c,构造函数g(x)=2-x,点(c,d)在函数图像上。g(x)为直线,f(x)为曲线,求过f(x)上一点与g(x)平行的切线即可。因切线斜率为-1,因此f′(x)=1-2ex=-1,可知x=0。切点坐标为(0,-2)。再计算该点到直线g(x)的距离平方为8。
=1,所以d=2-c,构造函数g(x)=2-x,点(c,d)在函数图像上。g(x)为直线,f(x)为曲线,求过f(x)上一点与g(x)平行的切线即可。因切线斜率为-1,因此f′(x)=1-2ex=-1,可知x=0。切点坐标为(0,-2)。再计算该点到直线g(x)的距离平方为8。
三、结语
构造函数法能帮助学生迅速厘清解题思路,快速解题,但由于该方法的应用有一定难度,因此教师应为学生总结应用要点:应用构造函数法解题时,应根据函数的周期性、奇偶性、单调性等知识点求解,因此学生必须扎实掌握函数基础知识。教师应从教学内容出发,让学生多做经典例题,引导学生积累解题技巧,不断提高学生对构造函数法的应用水平,促进学生解题能力的提升。
参考文献
[1]张卓斌.数学解题应遵循“多想少算”原则[J].数学通报,2021(1):60-62.
[2]张昆.构造函数解题教学设计示例[J].数学通报,2022(2):46-48.
[3]许秀亮.看形找数以数解形——谈平面解析几何试题解题策略[J].数学通报,2021(3):49-53,58.
[4]龙正武,秦玉波.提高学生代数解题能力的两点思考[J].数学通报,2020(3):25-27.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/48779.html

 ,可知函数f(x)在(-∞,-1)和(-1,+∞)递增。因不等式性质|a+b|≤|a|+|b|,因此
,可知函数f(x)在(-∞,-1)和(-1,+∞)递增。因不等式性质|a+b|≤|a|+|b|,因此
 在这类题目的证明中,教师应引导学生仔细观察题目,灵活使用构造函数法,再利用函数性质快速得出答案。
在这类题目的证明中,教师应引导学生仔细观察题目,灵活使用构造函数法,再利用函数性质快速得出答案。
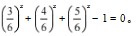 设函数
设函数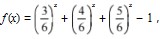 则f(1)=1,f(2)<1,f(3)=0,则原方程的一个根为x=3。因
则f(1)=1,f(2)<1,f(3)=0,则原方程的一个根为x=3。因 、
、 在R上是减函数,因此f(x)在R上是减函数,当x>3时,f(x)<f(3)=0,当x<3时,f(x)>f(3)=0。因此,原方程的唯一解为x=3。
在R上是减函数,因此f(x)在R上是减函数,当x>3时,f(x)<f(3)=0,当x<3时,f(x)>f(3)=0。因此,原方程的唯一解为x=3。 =
= =1。已知e是自然对数的底数,求(a-c)2+(b-d)2的最小值。
=1。已知e是自然对数的底数,求(a-c)2+(b-d)2的最小值。 =1,所以b=a-2ea,构造函数f(x)=x-2ex,点(a,b)在函数图像上。同理,因
=1,所以b=a-2ea,构造函数f(x)=x-2ex,点(a,b)在函数图像上。同理,因 =1,所以d=2-c,构造函数g(x)=2-x,点(c,d)在函数图像上。g(x)为直线,f(x)为曲线,求过f(x)上一点与g(x)平行的切线即可。因切线斜率为-1,因此f′(x)=1-2ex=-1,可知x=0。切点坐标为(0,-2)。再计算该点到直线g(x)的距离平方为8。
=1,所以d=2-c,构造函数g(x)=2-x,点(c,d)在函数图像上。g(x)为直线,f(x)为曲线,求过f(x)上一点与g(x)平行的切线即可。因切线斜率为-1,因此f′(x)=1-2ex=-1,可知x=0。切点坐标为(0,-2)。再计算该点到直线g(x)的距离平方为8。