角度 5 联想三角函数定义,转化为三角函数问题.
解法 5 如图 5,设 P( x,y)为圆 C:x2+ y2= 4y- 3 上一点,且∠POx = θ,又直线 l1 : 3 x + y = 0 和l2 : 3 x - y = 0 均与圆 C 相切,倾斜角分别为 120°,60°,则 θ∈[60°,120°].
解法 6 如图 5,以坐标原点为极点,x 轴非负半轴为极轴建立极坐标系,设 P( ρ,θ) 为圆 C 上一点,则 θ∈[60°,120°]



结合,当点 B 位于 B3 位置时,OA→在向量OB→方向上的投影取最大值,即为 OA→ = 3;当点 B 位于 B1 位置时,OA→在OB→方向上的投影为 2 2 ;当点 B 位于 B2位置时,OA→在向量OB→方向上的投影为根号 6 .

数学离不开解题 ,数学研究的过程就是解决问 题的过程 ,掌握数学的一个重要标志就是善于解题. 可见 ,解题是一名教者的必备技能 ,技能的形成并非 一朝一夕 ,而在于日积月累. 数学解题是巩固基础知 识、落实基本技能、感悟思想方法、提升思维敏锐度 的系统活动 ,所以对一道典型问题进行多角度的分 析与解答是非常必要的. 笔者从六个角度对一道清 华测试题予以分析 ,给出六种不同的解法 ,解法 1 是 在观察出分式的齐次化特征后 , 比值换元为一次函 数 ,再以导数为工具求函数最值. 解法2 至 5 是基于 函数式的结构特征 ,联想所学的基本概念、公式 ,构 造出函数式的几何意义解题 ,其中解法 2 和 3 联想 点到直线的距离公式 ,分别将函数式转化为直角三 角形内角的正弦值问题和距离问题 ;解法 4 联想向 量夹角余弦公式 ,转化为余弦函数问题 ;解法 5联想 三角函数定义 ,转化为三角函数问题. 解法 6 通过极 坐标换元法 , 同样将问题转化为三角函数问题 ,与解 法 5 异曲同工. 用多种方法解答同一道数学题 ,不仅 能更牢固地掌握相关的数学知识 ,还能更灵活地运 用所学知识 ,加强对数学整体性的理解与认识. 通过 一题多解 ,分析、比较各种解法 ,可以找到最佳的解 题途径 ,从而发散学生的思维能力 ,对巩固数学知识 和提高解题能力大有裨益.
4. 2 夯实基本知识 ,强化通性通法
《 普通高中数学课程标准( 2017 年版)》指出 : 在数学高考命题中 ,考查内容应围绕数学内容主线 , 聚焦学生对重要数学概念、性质、方法的理解和应 用 ,强调基础性 ;注重数学本质和通性通法. 因此 ,笔 者认为在日常的解题教学中 ,教师应加强基础知识、 基本技能和基本数学思想方法的训练 , 以提高学生 解题的基本活动经验. 我们寻求一题多解 ,但不能满 足于一题多解 ,更不能为了一题多解而多解 ,而是要 在解答的过程中总结出哪种方法适合哪类题型 ,选 择哪个方法更加合理、高效 ,对于一些常考题型 ,甚 至于必考题型 , 教师要指导学生总结该类问题的“ 通性通法”,形成解题模型. 通过文中对问题的多种解法不难看出 ,六种解法间的计算量和思维深度都有差别 ,但也都是解决类似分式函数的通法 ,那如何进行“通性通法”的训练呢? 笔者认为 ,所谓“ 通性通法”一定是建立在对问题形式、结构、特征等有着深刻理解的基础之上 ,在有多种方法选择的情况下 ,能快速找到最合理、高效的方法来完成解答. 在日常的解题教学中 ,教师要指导学生分析每一种解法的优与劣 ,打破总是求导判断单调性的类似经验解题的惯性思维 ,如解法 1 就是最常规解法 ,虽思路顺畅 ,但过程冗长、计算量大 ;解法 2 至 5 根据函数式结构特征 ,联想点到直线距离公式、向量数量积、三角函数定义式、数形结合解出题目 ;解法 6 直接极坐标换元 ,转化为三角函数问题 ,直接了当 ,干净利落. 因此 ,教师在解题教学中要指导学生如何根据问题特征 ,设计最合适的算理 ,选择最佳的解法 ,这样在平常的考试及最终的高考中才能“ 以不变应万 变”,顺利完成考试.
参考文献 :
[ 1 ] 教育部考试中心. 中国高考评价体系[M ] . 北 京 :人民教育出版社 ,2019 .
[2 ] 刘海涛. 一 个 二元条件极值问题的解法探析 [J ] . 中学数学研究( 华南师范大学版) ,2021 (03 ) :44 - 45 .
[3 ] 刘海涛 ,何浩成. 例谈极坐标换元法在二元最值 问题中的应用[J ] . 中学数学研究( 华南师范大 学版) ,2021( 15) :22 - 24 .
[4 ] 刘海涛. 重视解题教学 ,善于变式推广 ,探究通 解通法— 以 2020 年 全 国 卷 Ⅰ 导 数 题 为 例 [J ] . 数学教学研究 ,2021 ,40(02) :49 - 54 .
[5 ] 中华人民共和国教育部. 普通高中数学课程标 准(2017 年版) [ M ] . 北京 : 人民教育 出版社 ,2018 .

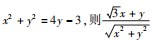 的最大值为( )
的最大值为( )
 - 3,得(k2+ 1) x2- 4kx + 3 = 0,由 Δ≥0,解得
- 3,得(k2+ 1) x2- 4kx + 3 = 0,由 Δ≥0,解得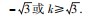

 知可将函数式理解为直角三角形内角的正弦值问题.角度 3 联想点到直线距离公式,转化为距离问题.
知可将函数式理解为直角三角形内角的正弦值问题.角度 3 联想点到直线距离公式,转化为距离问题.
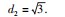


 角的余弦值与正弦值的和的问题.
角的余弦值与正弦值的和的问题.

 结合,当点 B 位于 B3 位置时,OA→在向量OB→方向上的投影取最大值,即为 OA→ = 3;当点 B 位于 B1 位置时,OA→在OB→方向上的投影为 2 2 ;当点 B 位于 B2位置时,OA→在向量OB→方向上的投影为根号 6 .
结合,当点 B 位于 B3 位置时,OA→在向量OB→方向上的投影取最大值,即为 OA→ = 3;当点 B 位于 B1 位置时,OA→在OB→方向上的投影为 2 2 ;当点 B 位于 B2位置时,OA→在向量OB→方向上的投影为根号 6 .
