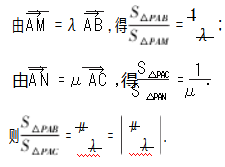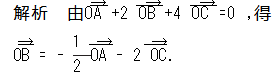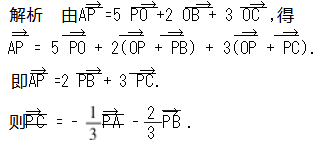平面向量中的三个结论及其应用论文

 

SCI论文（www.lunwensci.com）：

　　摘  要 :本文给出平面向量中涉及两个三 角形面积比 ,直角三 角形中数量积以及两个向量的三 角不等式等三个结论及其应用.

　　关键词 :平面向量;面积比;数量积;三角不等式

　　结论 1  点 P 是△ABC 所在平面上一点 ,=  ,λμ≠0 ,S △ 表示三角形的面积 ,则=  .
 

　　证明  (1)当 λ >0,μ >0 时 ,如图 1,在射线 AB, AC 取点M,N 使  ,以 AM,AN 为邻 边作▱AMPN,则   ,且 S△APM =S△APN.
 

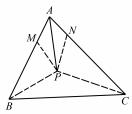
图１
 

　　

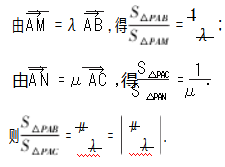
　　(2) 当 λ <0 ,μ >0 时 ,如图 2 ,在射线 BA,AC 上取点 M,N 使  ,以 AM,AN 为邻 边作▱AMPN,则  ,且 S △APM = S △APN.
 

图２
 

　　

　　(3) 当 λ >0 ,μ <0 时 ,同上可证 ;

　　(4) 当 λ <0 ,μ <0 时 ,同上可证. 由(1) (2) (3) (4)知命题成立.

　　例 1  已知 A,B ,C 三点不共线 ,且 （）


　　A.     B.     C. 6    D.

　　解析  由 及命题得 =,故选 C.
 

　　例 2  已知点 O 在 △ABC 的内部 ,且有 OA +2 OB +4 OC = 0 ,则 △OAB 与 △OBC 的面积的比值为
.

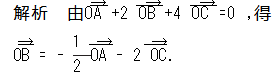
　　由命 题 得 △OAB 与 △OBC 的 面 积 的 比 值 为

　　例 3  已知△ABC 所在的平面内一点 P (点 P与点Ａ，Ｂ，Ｃ不重合，且则△ACP 与△BCP 的面积之比为(     ).

　　A. 2∶ 1    B. 3∶ 1    C. 3∶ 2    D. 4∶ 3

　　
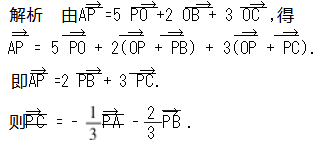
　　由 命 题 得 △ACP 与 △BCP 的 面 积 之 比 为 ,故选 A.


　　例 4  已知 △ABC 所在的平面内一 点 P 满足2 PA +5 PB + 3 PC =0 , △ABC 的面积为 S,则△PBC的面积为_____.

　　


　　由命题得

　　所以△PBC 的面积为 .
 

　　例 5  设 P ,Q 为△ABC 内的两点 ,且   +,,则△ABP 与△ABQ 的面积之比为(     ).
 

　　A. 1 ∶ 27    B. 1 ∶ 4    C. 4∶ 9    D. 1 ∶ 3

　　

　　由命题得△ABP与△ABQ 的面积之比为

　　

　　故选 C.

　　结论 2  如图 3 ,在 Rt △AOB 中 ,AB ⊥ OA,则
 

　　证明 

　　
 

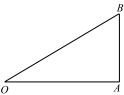
图 3
 

　　例 6  如图 4 ,在☉C 中 ,是不是只需知道☉C的半径或弦 AB 的长度 ,就可以求出AB ·AC的值?
 

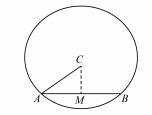
图　4

　　解析  取线段 AB 中点 M,连接 CM, 由圆中垂 径定理 ,得 CM⊥AB ,AM = MB.

　　由性质 ,得

　　

　　所以只需知道弦 AB 的长度 ,就可以求出的值.
 

　　例 7  如图 5 ,O 为△ABC 的外心 ,AB = 4 ,AC = 2 , ∠BAC 为钝角 ,M 是边 BC 的中点 ,则的值是(     ).
　　
　　A. 2 3  B. 12   C. 6    D. 5
 

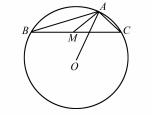
图 5

　　解析  由 M 是边 BC 的中点 ,得
　　
　　由性质及例 1 的解答过程 ,得

　　

　　故选 D.

　　例 8  据《九章算术》记载 ,商高是我国西周时 期的数学家 ,曾经和周公讨论过“勾 3 股 4 弦 5”的 问题 ,比毕达哥拉斯早 500 年. 如图 6 ,现有 △ABC满足“勾 3 股 4 弦 5”,其中 AC = 3 ,BC = 4 ,点 D 是CB 延长线上的一点 ,则 = (    ).

　　A. 3  B. 4    C. 9    D. 不能确定
 

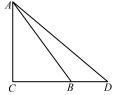
图 6
 

　　解析  由题意 ,得 AC⊥CB.由性质 ,得  = 32 =9.

　　故选 C.

　　例 9  在 Rt △ABC 中 , ∠ACB =  ,AC = BC = 2 ,点 P 是斜边 AB 上一点 ,且 BP = 2PA,则  ·→ CP.CA  →+ CP ·CB = (    ).

　　A. -4    B. -2    C. 2    D. 4
 

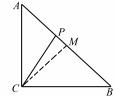
图 7
 

　　解析  如图 7 ,取线段AB 中点 M,由题意知 CM⊥AB ,且 CM =  2/1 AB =  2/1 = 2.
 

　　

　　注  由上述解答过程可知 ,例 9 中的点 P 若是 直线AB 上任意一点 ,均有 =4.

　　例 10  已知菱形 ABCD 的边长为 a, ∠ABC =


　　A. - a2    B. - a2    C. a2    D.a2
 

　　解析  设菱形 ABCD 的对角线 AC ,BD 相交于 点 O,由菱形的性质得 AC ,BD 垂直且相互平分.

　　由 ∠ABC =60° ,得

　　BD = 2BCcos30° = 3a OD =  3 /2a.

　　

　　故选 D.

　　例 11  在▱ABCD 中 ,AM⊥BD 于点M,AM = 3 , 则  = —— .

　　解析  设 ▱ABCD 的对角线 AC ,BD 相交于点 O,由平行四边形性质得 AC =2AO.

　　

　　结论 3  对于向量 a,b,有  a + b  ≤  a  +  b  , 等号当且仅当 a,b 共线且同向时成立.

　　例 12  如图 8 ,空间直角坐标系 O - xyz 中 ,正 △ABC 的顶点 A,B 分别在 xOy 平面和 z 轴上移动.若 AB =2 ,则点 C 到原点 O 的最远距离为(    ).
 

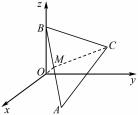
图 8
 

　　A. 3 - 1    B. 2    C. 3 + 1    D. 3

　　解析  取线段 AB 的中点 M, 由题意得 OB ⊥


　　由1 ,得点 C 到原点 O 的最远距离为 3 + 1 ,当且仅当O,M,C 三点共线时取最大值. 故选 C.

　　例 13  已知点 G 是△ABC 的外心 ,是三个单位向量 ,且 2  = 0 ,如图 9 所 示 , △ABC 的顶点 B ,C 分别在 x 轴的非负半轴和 y 轴的非负半轴上移动 ,O 是坐标原点 ,则 的最大值为(    ).

　　A. 2   B. 3   C. 2  D. 3

　　解析  如图 9 ,由 2 = 0 知 G 为线段 BC 中点 , ∠BAC = .
 

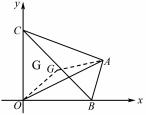
图 9
 

　　又 GA = GB = GC = 1 ,得 BC =2.

　　则 OG = CG = 1.

　　所以

　　例 14   在 平 面 直 角 坐 标 系 中 , O 为 原 点 , A( - 1 ,0) ,B(0 , 3 ) ,C(3 ,0). 动点 D 满足 = 1 ,则的最大值是————.

　　

　　例 15  已知函数则该函数的最小值为————.

　　解析  设 P(x2 ,x) ,A(2 ,5) ,B(3 ,0) ,则

　　→
　　PA=

　　→
　　PB  =  
 

　　→
　　PC==

　　由6得该函数的最小值为  ,等号当且仅当 P ,A,B 三点共线时成立.
 

　　参考文献 :

　　[1] 杜龙安. 例析平面向量在三 角形四心 中的应用 [J]. 数理化解题研究 ,2021(25) :40 -41.