SCI论文(www.lunwensci.com)
摘 要 : 向量数量积最值问题是高考常考的一类重要题型.解答此类型问题时,绝大多数考生 往往只会采用解析法以及公式法求解,其实向量数量积最值问题的解法是灵活多样的.基于此,本 文以 2020 年天津卷第 15 题第二空为例,从 8 种不同的视角入手,归纳出 9 种解法.
关键词 : 向量数量积,最小值,多解
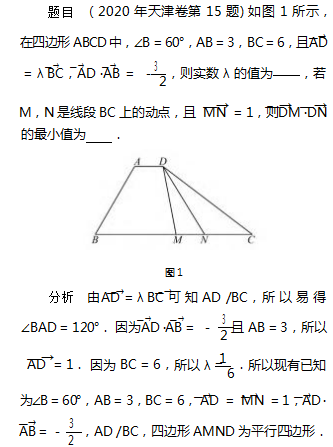
1 试题呈现
2 试题溯源
试题溯源可以帮助解答者加深对问题的认识, 从而寻求更多的解答方式. 向量数量积问题是高考 的热点问题,最小值问题深受命题者青睐.弄清问题 的源头,对于问题的多角度、多方法求解可以起到事半功倍的效果.
评注 例题与上海卷第 8 题都是向量数量积的 双动点问题,并且两动点之间都是固定距离且两向 量的起点都是固定的,两者的区别仅在于例题中向 量的起点是位于同侧的,上海卷第 8 题是位于异侧,但两者的解答方式与思想方法都是十分类似的.溯源 2 ( 2018 年天津理第 8 题) 如图 2,在平 面四 边 形 ABCD 中,AB ⊥ BC,AD ⊥ CD, ∠BAD =
评析 本例中点 E 为边 CD 上的动点,点 E 相 对于两定点 A,B ; 例题中点 D 为相对于两距离固定 的动点 M,N 的定点.运动是相对的,将两定点 A,B 相对于动点 E 运动看作距离固定的两点 A,B 为相 对于点 E 动点时,也就是例题.在 2015.2016.2018. 2019 年天津卷中文理科都考了向量的数量积,其中 2015 年文科 14 题与 2018 年理科第 8 题都是向量的 数量积的最小值问题.
3 试题多解
3.1 考虑基底法
何为基 底 法? 即用两条不共线的非零向量 表示这一平面内所有向量的方法. 在 具 体 问 题 中,往往不能直接对问题所求向量进行运算,这 时就需要运用基底法将所求向量进行合理转化, 最终方便运算.
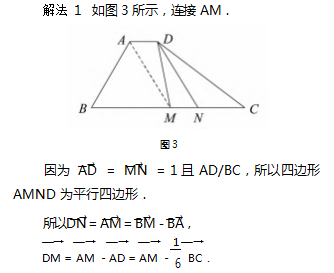
解法 1 如图 3 所示,连接 AM.
评注 由解法 2 中所设 M( t,0 ),N ( t + 1.0 ) 可 以看出,并不是所有点的坐标都是已知的,因此需要 设点的坐标.为了运算方便且过程简洁,在设点时应 当注意挖掘点的特殊性以及点与点之间的关系,尽 量减少未知数个数.
3.3 考虑余弦定理求两向量夹角余弦值
许多时候,向量数量积不能直接运算的主要原 因不在于向量模长的求取,而是两向量夹角余弦值 的未知.运用三角形余弦定理可以较为方便地求出 夹角的余弦值,因此,将余弦定理与向量数量积公式相结合.具体如下 :
评注 若是已知两向量模长,运用余弦定理可 以求得其夹角的余弦值,这样也就可以有效解决两 向量夹角余弦值未知或难求的问题.关键在于正确 运用余弦定理将两向量夹角的余弦值进行转化.
3.4 考虑将双动点转化为单动点
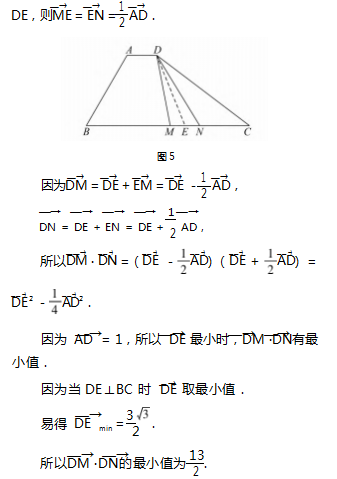
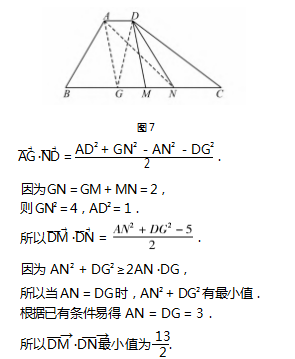
解法 4 如 图 5 所 示,取 MN 中 点 E 并 连 接
评注 例题中点 M 与点 N 虽为双动点,但两点 之间的距离是固定的,因此运用向量加法的三角形 法则将动点 M 与动点 N 转化为它们的中点 E,解法 4 亦可看作是分点恒等式的应用.
3.5 考虑向量中值定理
评注 向量中值定理是一个较为常用但是往往 被忽略的一个定理,在平行四边形中利用余弦定理 可以得到中值定理.
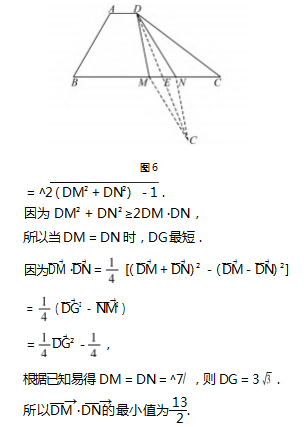
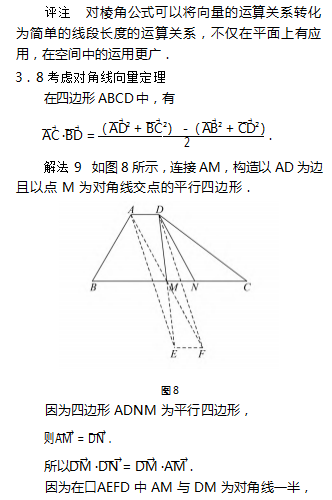
3.6 考虑极化恒等式
评注 对角线向量定理可以说就是向量数乘余 弦定理的组合或推导结论,在各地的高考试题都有 所体现.
纵观历年高考向量题,是没有屡试不爽的通法 妙招的.解答向量数量积最值问题的方法可以是多 样的 ; 除常规的基底法与解析法以外,可充分利用平 面向量几何意义从而构造几何图形,以及运用极化恒 等式、向量中值定理、对棱角公式等恒等式进行解答.
参考文献 :
[1] 徐达强,刘秋阳,刘成龙.2017 全国高考江苏卷理科 12 题的多解及推广 [J].理科考试研究, 2017.24 (21) : 5-7.
[2] 李一舟,殷伟康.平面向量最值问题的常见解题策略 [J].中学数学,2019 (07) : 50-52.
[3] 蔡小雄.更高更妙的高中数学思想与方法 ( 第10 版) [M].杭州: 浙江大学出版社,2018.
[4] 吴淑芳,朱成万.1 个公 式 5 类 问题 14 年 高考——— 对角线向量定理在浙江高考中的妙 用 [J].中学教研(数学) ,2017 (08) : 36-40.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66808.html