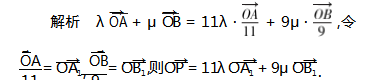平面向量等值线定理及其应用论文

 

SCI论文（www.lunwensci.com）：

　　摘  要 :本文梳理了等值线性质及如何求定值“k”,对等值线进行解读. 应用等值线解高考题 及竞赛题中出现的一类向量线性表示后的系数问题.

　　关键词 :等值线定理;等值线应用;平面向量
　
　　平面向量基本定理是向量坐标表示 , 以及向量 法求解几何问题的理论基础 , 由其引出了几个系数 等值线定理 ,笔者在高三复习教学时注意到 ,在解决 向量线性表示后的系数问题时 ,等和线与等差线能 让学生从形的角度去分析问题 ,解法直观 ,过程简洁 流畅 ,可以拓展思维 ,加深学生对平面向量基本定理 的理解 ,应用最为广泛 ,是解决此类问题的通法. 文 [1] 给出了定理的证明过程 ,下面整理性质并进行应用举例 ,供考生参考.

　　为表示定值“k”给出定义 :若 a ∥b ( b≠0 ) ,则  =   (a ,b 同向) ; = -    (a ,b 反向) .

　　1 等和线

　　1. 1 等和线定理

　　平面内一组基底 {   }  (x ,y ∈R) ,若点 P 在直线AB 或 l( l∥AB) 上 ,则 x + y = k ( 定值) ,反之亦成立. 直线AB及 l 称为等和线.

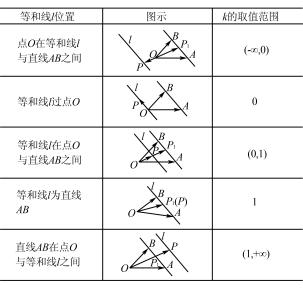
　　1. 2 等和线性质
 

表 1   等和线性质

 

　　见表 1 所示 , 当等和线过点 O 时 k = 0;当等和线不过点 O 时 ,k =  ,P1   为直线 OP 与 AB 的交点. 特别地 , 当等和线为直线 AB 时 , 即为三点共线定理 :平面内 一 组基底 { , }  (x ,y∈R) ,则 P ,A ,B 三点共线的充要条件是 x+ y = 1.
 

　　1. 3 等和线应用举例

　　例 1     ( 2016 年 河 北 赛 区 预 赛 6 ) 在 ΔABC 中 ,D 为边 BC 的中点 , 当动点 E 在线段 AD 上移 动时 ,若  ,则 s = λ 2  + μ 的最小值是_____.

　　解析
　　因为又 A ,D ,E 三点共线 ,故 λ + 2μ = 1.

　　所以 λ2  + μ = ( 1 - 2μ)2  + μ.

　　故当μ = 3/8 时 ,s 的最小值是 7/16.

　　例 2    (2010 年吉林赛区预赛 11)已知圆 O 的 半径为 1 ,半径 OA ,OB 的夹角φ(0 < φ < π) 为常数 , 点 C 为圆上动点 ,若  ,则 x + y 的最大值为____.
 

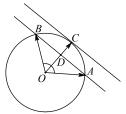
图 1

　　解析   , 由等和线定理 ,如图 1平移等和线AB 至与圆 O 切于点 C 时 ,x + y 取最大值 ,此时 x + y =.
 

　　又 | OD | = cos  ,故 x + y 的最大值为 .
 

　　例 3    ( 2017 年高考全国 Ⅲ 卷理 12 )在矩形 ABCD中 ,AB = 1 ,AD = 2 ,动点 P 在以点 C 为圆心且 与 BD 相切的圆上. 若  ,则 λ + μ 的最大值为(       ) 

　　A. 3       B. 2 2       C.  5       D. 2

　　解析   如图 2 ,根据等和线定理 ,平行移动等和线 BD 至 l ,使直线 l 与圆 C 切于点 P 时 λ + μ 最 大 ,过点A 作直线 l 的垂线 ,垂足为点 G ,不妨设圆 C 半径为 r ,AF = CH = r ,FG = 2r ,故 λ + μ = = = 3.
 

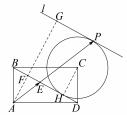
图 2

　　例 4    (2020 年四川赛区预赛4) 在直角坐标系 中 ,A(1 ,2) ,B(3 ,0) ,点 P 为圆(x - 3)2  + (y - 2)2 = 1 上任意一点 ,设) ,则 11λ + 9μ 的最小值是____-
 

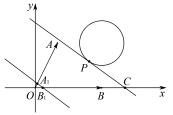
图 3

　　          
                             .
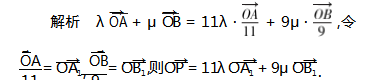
　　由等和线定理 ,如图 3 平移等和线 A1 B1  至与圆切于点 P 时 ,11λ + 9μ 最小 ,此时 11λ + 9μ =.

　　可求得切线 PC 方程为 3x + 4y - 12 = 0. 所以 | OC | = 4.

　　又 | OB1 | = ,故 11λ + 9μ 的最小值是 12.

　　例 5    ( 2017 年高考江苏卷 12 ) 如图 4 ,在同 一平面内 , 向量的模分别为 1 , 1 ,  2 , 与的夹角为 α ,且 tanα = 7 , 与 的夹角 为45 ° . 若  = m  + n ( m , n ∈ R) , 则 m + n= _____ .
 

　　解析  如图 4,连接 AB 交 OC 于点 D , 由等和线定理可知 m + n =.
 

　　在△AOB 中 ,tan∠AOB = -  4/3  ,故 sin∠AOB =  4/5
 

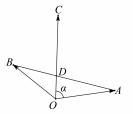
图 4
 

　　由 tanα = 7,得 sinα =  .
 

　　又 S △AOB  = S△AOD  + S△BOD ,　

　　即| OA | · | OB | · sin∠AOB

　
　　=  | OA | · | OD | sinα +  | OB | · | OD | sin45°. 解得 | OD | =  . 所以 m + n = 3.
 

　　2 等差线

　　2. 1 等差线定理

　　平面内一组基底 {  }   (x,y ∈R) , = - ,若点 P 在直线 AB1  或 l ( l∥ AB1 ) 上,则 x - y = k ( 定值) ,反之亦成立. 直线 AB1 或 l 称为等差线.
 

　　2. 2 等差线性质

　　见表2 所示,当等差线过点 O 时 k =;当等差线不过点 O 时,k = ,P1  为直线 OP 与 AB1  的交点.

　　2. 3 等差线应用举例

　　例 6    (2011 年辽宁赛区预赛 8) 直线 3 x - y -3 = 0 与抛物线 y2  = 4x 交于 A,B 两点 , ( 点 A 在 x 轴上方) ,与 x 轴交于点 F,若 ,则 μ2  - λ2  = ____.

表 2   等差线性质

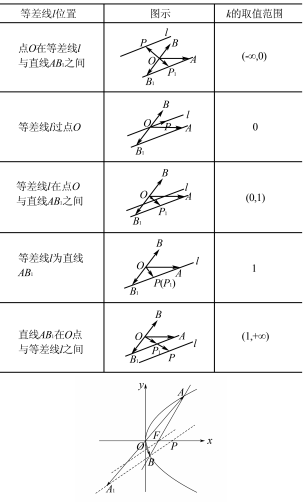
图 5
 

　　解析   联立直线 AB 与抛物线方程可得 A (3 ,2 3 ) , B (  , -  ) , 作的相反向量 , 即A1 ( - 3 , - 2 3 ) .
 

　　如图 5,连接 A1 B 与 x 轴交于点 P,由等和线定 理,点 F 在等和线 AB 上,故 μ + λ = 1. 由等差线定理,平移等差线 A1 B 过点 F,则 μ - λ =.

　　又直线 A1 B 方程为 y =(x - 2) ,
 

　　令 y = 0 得 P(2 ,0) .

　　又 F(1 ,0) ,所以μ - λ =  . 即 μ2  - λ2  = .

　　例 7     在 ΔOMN 中 ,若，点 P 落在四边形ABNM 内( 含边界) ,则的取值范围是____.
 

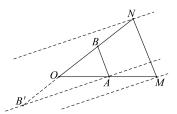
图 6
 

　　解析  如图 6 , 由等和线定理 ,平行移动等和线 AB 至 MN ,可得 x ,y 需满足 1 ≤x + y≤2.

　　由等差线定理 ,平行移动等差线 AB′ , 当等差线 过点 M 时 , (x - y)max   = 2 , 当 等 差 线 过 点 N 时 ,(x - y)min  = - 2 ,得 x ,y 还需满足 - 2≤x - y≤2.

　　即 x ,y 需同时满足


　　由线性规划知识 ,为以上不等式组所表示可行域中的点P(x ,y) 与点( - 2 , - 1) 连线的斜率 ,故∈ [ ,] .

　　3 对等值线的解读

　　定理中系数取定值的等式分别为 x + y = k ,x - y =k ,与平面直角坐标系中的直线方程形式完全一 致 ,而且系数取定值时点 P 轨迹也是直线 ,难道是巧合吗?

　　显然不是. 当平面内一组基底{ OA ,OB} 是单位正交基底时 ,通过构建以为标架的平面直角坐标系，，有序实数对（x,y）就是点p的坐标，也是的坐标，事实上 , 当平面内一组基底{ OA ,OB} 不是单位正交基底时 ,参照仿射几何知识 ,也可以通过构建以{ O ;OA→，为标架地 平面仿射坐标系，使该平面内的任一点点同样地与有序数对(x ,y) 建立起一一对应关系.需要注意的是 ,与平面直角坐标系不同 ,平面仿射坐标系两轴单位长度无需相同。那么向量 ,也就会对应唯一 的平面仿射坐标 系坐标(x ,y) .

　　在平面仿射坐标系中 ,直线方程也同样是二元 一次方程. 这就不难解释两种等值线为什么是直线了. 事实上 , 这两个系数取定值的等式正是以 { O ; 为标架的平面仿射坐标系中点 P 的轨迹方程;这两种等值线正是在以{ O;OA ,OB} 为标架的平 面仿射坐标系中的方程所对应的曲线. 那么我们可 以想到 ,除了这两种等值曲线外 ,应该还有满足其它 条件的等值曲线 , 比如等积线、等商线、等平方和线 , 其实质是平面仿射坐标系中满足条件的轨迹曲线.

　　基于以上认识 ,类比平面直角坐标系中的相关 概念 ,在对应的平面仿射坐标系中 ,对等值线中的k 可以赋予一定的几何意义. 等和线方程 x + y = k 变 形为 y = - x + k ,则 k 对应的就是“纵截距”;等差线 方程 x - y =k 变形为 y = x - k ,则 k 对应的就是“纵 截距的相反数”. 至此 ,我们从另一角度更深刻地认 识了平面向量基本定理系数等值线 ,也可以理解并 记忆不同图形所对应的k 的取值情形.

　　通过以上实例 ,我们可以发现运用等值线定理 解题时 ,首先三个向量应该共起点 ,对于没有共起点的问题 ,可以通过寻找相等向量转化进而求解. 其次 ,解题时通常是先找到基底{ OA , OB}下的“ 基准线”,也就是 k = 1 时的等值线 ,然后平行移动等值 线 ,利用图形几何特征 ,快速找到与“ 基准线”平行 的特殊等值线 ,再利用文中给出的公式求出对应 k 值 ,通过将向量问题转化为几何问题 ,使向量分解后 的系数问题以直观形象的方式得以圆满解决.

　　参考文献 :

　　[ 1 ] 潘成银. 平面向量基本定理系数等值线[J ] . 数 学通讯( 下半月) ,2013(02) :40 - 43 .