SCI论文（www.lunwensci.com）:
摘要:纵观条件中含有导函数与抽象函数的不等关系的题型，发现题设条件所给出的式子往往都是一阶线性微分方程的一部分，在高观点下，笔者揭示此类问题的本质，为解决此类问题提供参考.
关键词:高观点；构造法；导数压轴题；本质
1 问题的提出
例 1 (2015 年全国高考Ⅱ卷第 12 题)设函数f ′(x )是奇函数f(x )(x ∈R)的导函数，f(－1 ) ＝0， 当 x >0 时，xf ′(x )－f(x ) > 0，则使得函数f(x ) > 0成立的 x 取值范围是( ) .
A. (－1，0) ∪(1，＋∞ ) B. (－∞，－1) ∪(0，1)
C. (－∞，－1) ∪(1，＋∞ )D. (－1，0) ∪(0，1)
上例中出现了“xf ′(x )－f( x ) > 0”的结构式， 解决此类问题需要构造辅助函数. 对于此类题目，有一些常见结构式的辅助函数构造方法:
(1)若f(x ) ＋xf ′(x ) > 0(或 < 0)，可构造辅助 函数 g(x ) ＝xf(x )；
(2)若f(x ) －xf ′(x ) > 0(或 < 0)，可构造辅助函数 g(x ) ＝
；
(3)若 nf(x ) ＋xf ′(x ) >0(或 <0)，可构造辅助 函数 g(x ) ＝xnf(x )；
(4)若 nf(x ) －xf ′(x ) >0(或 <0)，可构造辅助函数 g(x ) ＝
；
(5)若f(x ) ＋f ′(x ) > 0(或 < 0)，可构造辅助 函数 g(x ) ＝exf(x )；
(6)若f(x )－f ′(x ) > 0(或 < 0)，可构造辅助函数 g(x ) ＝
；
(7)若f(x ) －tanxf ′(x ) >0(或 < 0)，可构造辅助函数 g(x ) ＝
.
在日常教学中，教师一般会要求学生熟记以上 常见结构式的辅助函数，然后再加以训练来巩固记 忆，然而，此类题目往往只有少数学生能够成功解 决. 问题的关键在于，如何去构造这样的辅助函数? 构造方法是怎样的? 有没有一般的步骤呢?
2“辅助函数”的构造原理(基于不定积分原理)
对于结构为 y′＋P(x )y ＝Q(x )的方程，结合求 导法则[ u (x )v (x ) ] ′ ＝u ′(x ) v (x ) ＋u ′(x ) v (x )，将 方程两端同乘以一个非零因子 r (x )，得
此时函数 ｇ(ｘ)的导函数中包含方程的左边部分 Ｐ(ｘ)ｙ ＋ ｙ′，而在高中相关类型导数题中往往给出了这部分与零之间的不等关系，从而可以判断出函数 ｇ(ｘ)的单调性，进而结合函数知识求解.
此时函数 ｇ(ｘ)的导函数中包含④式的左边部分 ｙ′ ＋ Ｐ(ｘ)ｙ － Ｑ( ｘ)，而在高中相关类型导数题中往往给出了这部分与零之间的不等关系，从而可以判断出函数 ｇ(ｘ)的单调性，进而结合函数知识求解.
此类结构的构造原理，基于不定积分的相关方法，读者可以深入了解，也可略过.
３ 结构为 Ｐ(ｘ)ｆ(ｘ) ＋ ｆ ′(ｘ)的类型
所以 ｇ(ｘ)在(０， ＋ ∞)上单调递增.
由于函数 ｆ ( ｘ) 为奇函数且 ｆ ( － １) ＝ ０，所以ｇ(ｘ)为偶函数，且 ｇ( － １) ＝ ｇ(１) ＝ ０.
因此，ｇ(ｘ)在(０， ＋ ∞)上单调递增，在( － ∞，０)上单调递减. 要求函数 ｆ(ｘ) > ０ 成立的 ｘ 取值范围，则 ｘｇ(ｘ) > ０，易知 ｘ∈( － １，０)∪(１， ＋ ∞)，故选 Ａ.
下面对结构式为 Ｐ(ｘ)ｆ(ｘ) ＋ ｆ ′(ｘ)类型的算法步骤进行总结:
(１)将题设条件中的结构式化归为 Ｐ( ｘ) ｆ( ｘ)＋ ｆ ′( ｘ)，即让“ ｆ ′ ( ｘ)” 的系数变为 １； (２) 找到Ｐ(ｘ)，并借助导数公式寻找其一个原函数 φ( ｘ)；(３)构造辅助函数 ｇ(ｘ) ＝ ｅφ(ｘ)·ｆ(ｘ).
按照上述步骤，我们再来看一看常见结构的构造方法:
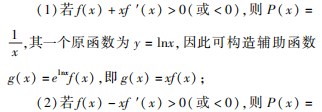
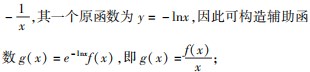
下面对结构式为 ｆ ′(ｘ) ＋ Ｐ(ｘ) ｆ( ｘ) － Ｑ( ｘ)类型的算法步骤进行总结:
(１)将题设条件中的结构式化归为 ｆ ′( ｘ) ＋Ｐ(ｘ)ｆ(ｘ) －Ｑ(ｘ)，即让“ｆ ′(ｘ)”的系数变为１；(２)找到Ｐ(ｘ)，并借助导数公式寻找其一个原函数 φ(ｘ)；(３)利用求导公式寻找 ｅφ(ｘ)Ｑ(ｘ)的一个原函数 ψ(ｘ)；(４)构造辅助函数 ｇ(ｘ) ＝ ｅφ(ｘ)·ｆ(ｘ) － ψ(ｘ).
此类问题一般出现在选择题或填空题的压轴题位置，难度较高，其难点在于构造出“辅助函数”. 经过本文的探究，找到了构造相应“辅助函数”的一般步骤，将难点转化为“逆用导数求导公式，寻找导数的原函数”.
参考文献:
[１] 何尚凯. 浅谈一阶线性微分方程的解法[ Ｊ]. 高考，２０１８(２６):２０３.
[２] 宿晶. 构造函数在解决导数问题中的运用策略和技 巧 [ Ｊ ]. 数 理 化 解 题 研 究， ２０１６ ( １６ ):１５ － １７.
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/45154.html
