SCI论文(www.lunwensci.com):
摘 要 :整体法是一种思考问题的重要方法. 在高中物理习题教学中,有着很广泛的应用. 新课 程对学生思维能力有更高的要求,为提高学生掌握运用整体法解答物理问题的意识,更好的把握相 关细节,应做好整体法理论知识的讲解,并展示整体法在不同物理问题中的应用.
关键词 :整体法;物理;解题;应用
高中物理解题中有时可以将若干对象看成一个 整体,运用物理知识分析问题,能大大降低分析问题 的难度,促进解题效率的提升,因此教学实践中应注 重为学生系统地讲解整体法,为其更好地应用于解 题中奠定坚实的基础.
1 用于解答平衡类问题
平衡类问题是高中物理中很重要的一类问题. 关键在于合理的选取研究对象,运用受力分析列出 平衡方程. 其中选取研究对象时运用整体法能更好 的把握研究对象的整体受力情况,降低构建物理平 衡方程的难度,达到顺利解题的目的.
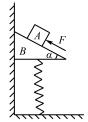
例如,如图 1 所示,三角形斜劈 B 紧靠墙壁放 在弹簧上. 将物块 A 放在 B 上. 起初 A 、B 均静止. 某 时刻使用力 F 沿斜面方向向上推 A,但 A 、B 均未动,则施加 F 后以下判断正确的是( ) .
A. A 、B 间的摩擦力一定变大
B. B 和墙之间可能无摩擦力
C. B 和墙面间的弹力可能不变
D. B 和墙面间的弹力变大
图 1
开始时对 A 进行受力分析,其受到重力,B 的支 持力,B 对 A 的静摩擦力f=mgsinα,处于静止状态.当施加力 F 后,若 F =2mgsinα,此时其静止,AB 间 的摩擦力的大小也为 mgsinα,A 项错误. 将 AB 看成 一个整体,开始时弹簧弹力和 AB 两者的重力相等, B 和墙壁无摩擦. 当施加 F 后,AB 仍静止,弹簧弹力 不变. 但是 AB 受到力 F,因此,B 受到墙壁的摩擦力大小为 Fsinα,方向竖直向下.
综上分析 D 项正确.
2 用于解答连接体类问题
高中物理中将轻绳、轻杆、弹簧等将物体连接起 来的一类问题通称为连接体类的问题. 因连接体的 局部和整体是统一 的,因此,解答该类问题常使用整 体法. 将若干研究对象看成一个整体,运用物理知识 求解出相关参数,以此为桥梁,便可分析、计算出连 接体中各研究对象的相关参数. 教学中为使学生体 会到运用整体法解答连接体类问题的便利,养成运 用整体法解题的良好习惯,应注重与学生一起剖析 相关的例题.
例如,如图 2 所示,使用轻绳将由相同材料制成 的 m1,m2 连接在一起,放置在斜面上. 在恒力 F 作用 下,沿斜面向上做匀加速直线运动,下列关于轻绳的拉力说法正确的是( ) .
A. 和斜面倾角 θ 有关
B. 和物体与斜面的动摩擦因数 μ 有关
C. 只和物体的质量 m1 有关
D. 若 F 沿斜面向下拉连接体,则轻绳拉力和θ、 μ 无关
图 2
当 F 沿斜面向上拉连接体时,将 m1 、m2 看成一 个整体,设加速度为 a,根据牛顿第二定律 :
F -( m1 +m2 )gsinθ-μ( m1 +m2 ) gcosθ = ( m1 +m2 ) a;
以 m2 为研究对象,设轻绳的拉力为 T,根据牛顿第二定律 :
T-m2 gsinθ-μm2 gcosθ=m2 a,
联立解得 T=
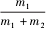
F.
同理当 F 沿斜面向下拉连接体时由 :
F+ ( m1 +m2 )gsinθ-μ( m1 +m2 ) gcosθ = ( m1 +m2 ) a ′,
T′+m1 gsinθ-μm1 gcosθ=m1 a ′,
联立解得 T′=
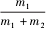
F.
综上分析可知选择 D 项.
3 用于解答相对运动类问题
相对运动 是 高 中 物 理 中 不 易 理 解 的 运 动 题 型. 解答该 类 题 型 的 思 路 较 多,解 题 中 只 有 具 体 问题具体 分 析,灵 活 运 用 多 种 解 题 方 法,才 能 少 走弯路. 其中运用整体法将整个运动过程看成 一 个整体,从能量的角度进行分析可获得事半功倍 的解题效 果. 教 学 中 应 注 重 经 典 例 题 的 讲 解,使 学生掌握运用整体法分析相对运动类问题的思路与技巧.
例如,如图 3 所示,倾角 θ =30° 光滑足够长的 斜面固定在水平面上,下端固定一挡板(和斜面垂 直) . 将可视为质点的物块放在木板的左端,一起放在 斜 面 上. 其 中 物 块 和 木 板 的 质 量 m 相 等 均 为1kg. 物块和木板的动摩擦因数
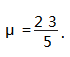
开始时木板下端和挡板的距离 L =0 . 9 m. 由静止释放物块 和木板,使 其 一 起 沿 斜 面 下 滑. 木 板 和 挡 板 碰 撞 的时间极 短,发 生 弹 性 碰 撞,物 块 恰 好 末 滑 离 木 板. g = 10m/s2,最大静最大静摩擦力等于滑动摩 擦力. 求 :
(1)木板和挡板第一次碰撞前的瞬间速度 v0;
(2)木板的长度 s.
图 3
(1)将物 块 和 木 板 看 成 一 个 整 体,根 据 动 能 定理 :
2mgLsin θ=

×2mv0 2
代入数据解得 v0 =3 m/s.
(2)木板和挡板会不断的碰撞,物块会一直在 木板上向下运动. 直到系统的能量完全消耗,木板停 在挡板位置,物块停在木板右端. 因木板和挡板碰撞 前后无能量损失,因此,以整个过程为研究对象,由能量守恒可得 :
μmgscosθ=mgLsin θ+mgsin θ(L+s )
代入数据解得 s =9 m.
4 用于解答电路类问题
动态电路分析是高中物理的常考知识点. 解答 相关习题时运用整体法可使得问题顺利的突破. 运 用整体法把握电路中相关参数的整体变化趋势,然 后结合电路的串并联特点以及电学元件所处的位置 灵活运用欧姆定律,便可分析出相关物理参数的变 化规律. 教学实践中,应注重为学生深入的讲解相关 的例题,使其把握应用整体法解答电路类问题的相 关细节.
例如,如图 4 所示,R1 、R2 、R3 为定值电阻,阻值 均为 R,滑动变阻器的阻值范围为 0 ~ 2R,电源电动 势为 E,内阻为 r,则滑动变阻器滑片按照以下方向 滑动时,判断正确的是( ) .
图 4
A. a→b 时,A 表示数变小
B. a→b 时,V 表示数变大
C. a→b 时,R1 消耗的电功率增大
D. 由 b → a 时,滑 动 变 阻 器 电 功 率 先 增 大 后变小
滑动变阻器滑片由. a → b 时,有效电阻变小,从 整体上来看,由欧姆定律可知干路电流增大,路端电 压变小,选项 A、B 错误. 由于流经 R1 的电流变小,则 消耗的功率变小,选项 C 错误. R1 支路的电流变小, 但干路的电流是变大的,因此,流过电流表的电流变 大. 滑动变阻器滑片由 b → a 时,接入电路中的阻值 将会从 0 逐渐增大至 2R. 将定值电阻和 r 看成一个整体,等效为电源内阻,则 r等效 =

≈R,则变阻器阻值为 R 时电功率会大,因此滑片滑动 的过程中电功率先增大后减小.
选择 D 项.
整体法是一种较为常用的解题方法. 教学实践 中为使学生牢固地掌握并灵活地应用于解题中,既 要做好整体法相关理论知识的灌输,优选精讲相关 的例题,又要引导学生做好听课的总结以及课下的 及时训练,不断的积累运用整体法解题的经验,提高 应用整体法解题的能力.
参考文献 :
[ 1 ] 刘家祥. 整体法在高中物理解题中的应用[ J ] . 数理化解题研究,2021 ( 16) :79-80 .
[2 ] 李燕. 推理法在高中物理解题中的有效应用 [J ] . 高中数理化,2021 ( 10 ) :45-46 .
[3 ] 陈碧. 整体法在高中物理解题中的应用[ J ] . 中 学生数理化(学习研究),2017 (01 ) :20 .
[4 ] 赵彬. 高中物理力学解题中整体法的应用方法 分析[J ] . 名师在线,2020(21 ) :68-69 .
[5 ] 张维平. 高中物理解题的整体法和隔离法的应 用 [J ] . 高中数理化,2020( 14 ) :32 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/45148.html

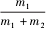 F.
F.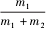 F.
F.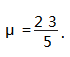 开始时木板下端和挡板的距离 L =0 . 9 m. 由静止释放物块 和木板,使 其 一 起 沿 斜 面 下 滑. 木 板 和 挡 板 碰 撞 的时间极 短,发 生 弹 性 碰 撞,物 块 恰 好 末 滑 离 木 板. g = 10m/s2,最大静最大静摩擦力等于滑动摩 擦力. 求 :
开始时木板下端和挡板的距离 L =0 . 9 m. 由静止释放物块 和木板,使 其 一 起 沿 斜 面 下 滑. 木 板 和 挡 板 碰 撞 的时间极 短,发 生 弹 性 碰 撞,物 块 恰 好 末 滑 离 木 板. g = 10m/s2,最大静最大静摩擦力等于滑动摩 擦力. 求 :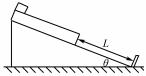
 ×2mv0 2
×2mv0 2
 ≈R,则变阻器阻值为 R 时电功率会大,因此滑片滑动 的过程中电功率先增大后减小.
≈R,则变阻器阻值为 R 时电功率会大,因此滑片滑动 的过程中电功率先增大后减小.