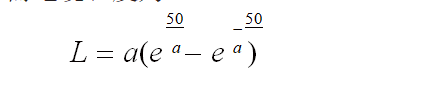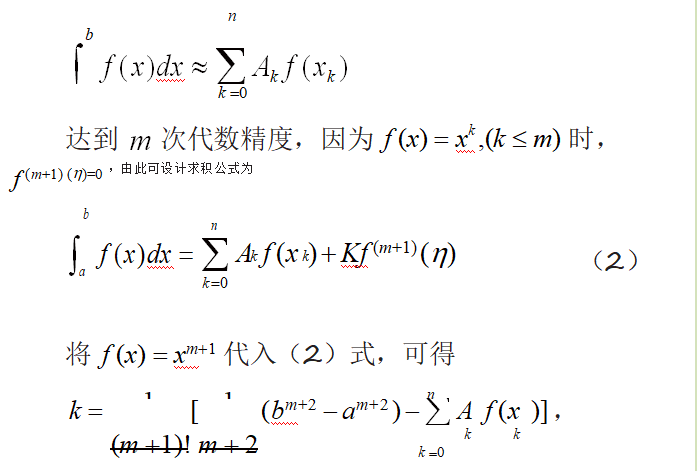SCI论文(www.lunwensci.com):
摘 要:数值分析是理工科的专业基础课,具有很强的实用性。本文针对课程的特点和教学实践,提出了数值分析课程建设的一些创新方法。从提升教学理念着手,改进教学方法,优化教学内容,强化实践教学,构建以学生自主学习为本,教师引导为辅的教学模式,激发学生学习的主观能动性,培养学生的思维意识和创新能力。
关键词:数值分析;教学改革;创新意识;应用能力
本文引用格式: 何俊红 . 基于创新型培养模式的《数值分析》课程教学改革与实践 [J]. 教育现代化 ,2021,8(41):87-90.
Teaching Reforms and Practices of “Numerical Analysis” Based on Innovative Training ModeHE Junhong
(Institute of Mathematics and Information Science, Baoji University of arts and Sciences, Baoji Shaanxi)
Abstract: Numerical analysis is a professional basic course for science and engineering, and it has strong practicability. According to the characteristics and teaching practice of the course, some innovative methods for the construction of numerical analysis courses are proposed. Starting from the promotion of teaching concepts, improving teaching methods, optimizing teaching content, strengthening practical teaching, constructing a teaching model based on student training and supplemented by teacher guidance, stimulates the subjective initiative of students in learning, and cultivates students’ thinking consciousness and innovative ability.
Keywords: numerical analysis; teaching reform; innovative consciousness; application ability
一 引言
随着高校教育改革的不断深入,以及社会对于应用型人才需求的不断增加,这就对在实际教学中不断重视和加强学生创新能力的培养,提出了更高的要求。培养创新型人才就是要将原来的以“教” 为主的教学模式转变为以“学”为主的翻转模式, 充分突出学生主体地位,在教与学的过程中让学生学会用科学方法认识、理解、掌握和运用知识,进而以自我为主体开展实践和创新。
“数值分析”是数学科学与计算机密切结合的实用性很强的一门基础课程,它是培养学生思维能力、计算能力、应用能力和创新能力的重要载体。根据社会对学生综合文化素质及全面能力的更高要求, 针对数值分析的特点,在教学中既要重视对算法的基本思想、概念和方法学习,又要关注学生运用数值方法解决实际问题的意识。这样不仅提高学生的理论分析和算法设计能力,又培养学生逻辑思维能力,确保学生与时代和社会发展需求相适应 [1-3]。因此,对学生创新能力和广泛应用意识的培养应该是该课程教学的落脚点。
二 数值分析课程面临的问题
(一) 当前的教学理念比较传统,不适应时代的发展
数值分析是数学科学与计算机技术密切结合的实用性很强的数学课程,既有纯数学的抽象性和严密性,又有应用的实操性和广泛性。学生在掌握好理论知识的基础上,通过数值实验加深对理论知识的理解,将数值算法理论知识与实际应用有机结合, 培养学生应用所学知识解决实际问题的能力。
目前, 国内许多高校在数学类课程的教学中,仍然采用传统的教育理念和方法进行教学。传统的灌注式教学模式只注重对书本知识的讲授,这样学生对于数值算法的理解仅停留在表层,认识和理解不深入、不透彻,同时学生对授课内容和方式感觉枯燥乏味, 不能引起学生学习兴趣。在教学中不能引导和调动学生主动思考、不利于发挥学生潜能,影响了学生对该课程的接受程度,致使学生在学习过程中缺乏对知识的兴趣和进一步探索精神。
目前,大部分数值分析课程教学在对学生应用能力和实践能力的培养方面比较欠缺,从而使得学生把学到的知识与实际生活应用不能有效的衔接, 这在一定程度上让学生对所学数学知识的实效性感知大大地降低,不利于培养学生创新思维和对知识的实践应用。
(二) 教学内容以及教学方法中存在的不足
数值分析是在学生必修了数学分析、高等代数等课程的基础上开设的课程,教学内容多,知识面跨度大,涉及范围广,有着难度大、抽象度高等特点, 客观上要求学生应具有一定的数学理论基础。目前, 开设的数值分析课程偏重于理论,一方面,学生前期的数学基础参差不齐,学生学习的主动性不高; 另外,学生反映课程中计算公式繁琐复杂,不易记忆, 而且算法的推导和分析有一定的难度,教学内容与实际应用脱节,学生感觉学习比较吃力,教学效果不佳。随着社会的发展,我们应当思考如何提高教学内容的实用性和可操作性。
传统的教学模式重理论推导,轻实践应用,重知识体系,轻探索研究,重知识传授,轻自主学习。在教学方法上只注重算法、数学原理的推导,对知识的应用和实践重视不够,教师以理论知识讲授为主,把一些基本的算法理论讲授给学生。学生只进行填鸭式的记忆,在数值实验环节,仅简单地介绍一些算法和验证性的实验,缺少创新性锻炼,学生对这样的讲授方式感觉枯燥和不感兴趣,学习效果不理想,也不利于学生对知识的深层理解,严重制约了学生独立思考和创新思维能力的培养。
三 数值分析课程教学改革的思路
计的全过程,刘徽在《九章算术注》中指出:“事类相推,各有攸归,故枝条虽分而同本干者,知发其一端而已”[1]。表明数值算法有着共同的基本规律可循,而掌握了基本规律,就能举一反三,触类旁通。近几年,随着高校不断扩张的影响,生源质量有所下降,学生的差异比较大,而当前高校教学普遍面临着班级学生数额较大,学情复杂等特点。在实际教学中,我们应该尊重学生个体差异,注重个性发展,充分体现“以学生发展为中心”的教育理念。利用课堂、微信、QQ 等方式了解学生学习基础、意愿、困难及未来发展方向等,根据学生实际差异,分类别、分层次有针对性地进行学习任务的分配,同时,强化学生思维能力和程序设计能力的训练。对学习能力、程序设计能力比较强的学生,引导、推荐参加大学生数学建模大赛、软件设计大赛、创新创业大赛等实践活动,培养和挖掘学生自主学习和应用知识的潜力。
“学起于思,思源于疑”,有疑问才能激发学生的求知欲。在实际教学中,采用启发式教学、互动式教学,让学生借助于各种教学资源,发挥学习的主观能动性,去学习如何解决学习中的疑问,提高发现问题解决问题的能力,最终把学生培养成为自我学习的主体 [4]。
(二) 引入真实案例,增加课程的实用性
数值分析理论性强,而且各章节之间衔接少, 单纯地进行理论分析,推导算法,学生只能被动地记忆一些数值算法,很难真正理解它,慢慢就缺乏学习的激情。在教学中,教师可根据教学内容适当地增加实际案例,让学生带着问题学习,培养学习的兴趣。
例如,在学习非线性方程求根时,提出问题: 在相距 100 米的两个塔(高度相同)之间悬挂一根电缆,允许电缆在中间最多下垂 1m,计算所需电缆的长度 [1]。通过分析题意,建立坐标系,由悬链线方程得到关系式由上述方程解出 a 后,根据弧长计算公式,所需电缆长度为
此问题的关键是要解出 a 值,而方程(1)是超越方程,用一般方法求解困难,需采用迭代法求解。诚然,每个算法都需要进行严谨的推导证明,但推导分析往往会让学生觉得繁琐且不易理解。因此, 设计收敛的迭代算法,通过编程,实现近似解序列的逼近过程,让学生体会迭代法的实用性,进而深刻理解迭代法的收敛性与收敛速度的相关理论知识。例如,在学习样条插值时,让学生将左手张开放置于显示屏前,通过鼠标输入的方式选择若干点, 利用这些数据可以绘出你的手形曲线。采用问题驱动教学,使其对所学内容与实际问题相联系起来, 将被动式教学转化为与学生互动教学。根据需要大力推进案例教学,通过实际问题讲解数值算法的基本思想和理论,辅助更加生动形象的教学模式,全方位满足学生的需求,提高数值分析课程的教学效果,进而培养学生分析和解决实际问题的能力。
通过案例教学,学生就不会感到数学课的枯燥和抽象,能更深刻地理解数值算法的思想和应用, 同时对学生数学运用能力的提高起到显著促进作用。
(三) 融入思政元素,培养学生的爱国精神
数学教学并不只是单调和抽象的理论课程,其实也是一个充满智慧和人文情节的课程。习近平总书记十分重视爱国主义教育,指出:“要用好课堂教学这个主渠道,使各类课程与思想政治理论课同向同行,形成协同效应”。在讲授《数值分析》课程时要重视思政元素的发掘和精选,遵循“因事而化, 因时而进,因势而新”的原则,不断完善数值分析课程的改革推进工作。
在讲解高斯消元法时,强调我国数学史上一部重要的数学经典《九章算术》,距今已有2千多年了,它在世界数学史上最早提出了线性方程组的程序化解法。它的出现标志着我国古代数学在中世纪达到的最高水平,以此激励学生奋发学习, 攀登数学高峰。数值求积的 Romberg 算法是对复化梯形公式逐次区间半分和逐次外推得到的算法,显著提高了计算结果的精度,其加速效果是奇妙的。在全国各地疫情防控阻击战中,运用趋势外推法的思想追溯病源,切断传播路径。中国行动速度之快世界罕见,展现出中国速度,中国效率。这就是所说的,有一种力量,叫中国力量,有一种速度,叫中国救援,以此激发学生爱国主义自豪感。
(四) 优化教学内容,培养学生的创新意识
数值分析的教学内容丰富,而教学时数在不断减少,面对学时有限的实情下,不可能将所有的知识点细致地讲解。必须因材施教,对教学内容上进行合理取舍。授课中要精心设计教学内容,突出讲授典型的、具有代表性的数值算法和原理,强调算法的构造思想和原理,潜移默化地让学生领会算法的思想和实质,培养学生的探索创新精神。
插值方法的思想很简单,把插值函数表示成一组基函数的线性组合。因此,构造插值函数的核心是构造插值基函数。引导学生针对问题的需求,寻找基函数所满足的条件,问题也就迎刃而解了。在这一章的教学中,可以对拉格朗日插值的思路过程进行细致地讲解,而对泰勒插值、牛顿插值、埃尔米特插值等等让学生自己探究它们的类似与差异之处,掌握不同插值方法适用的条件及近似的效果。让学生明白拉格朗日插值与牛顿插值是解决同一问题的不同方法,泰勒插值是牛顿插值的极限形式, 埃尔米特插值是泰勒插值与拉格朗日插值的综合和推广。
由于泰勒插值的条件苛刻,而拉格朗日和牛顿插值对于函数的近似程度还不够,由此引出了埃尔米特插值;学生通过实践特殊函数的拉格朗日插值,发现龙格现象,此时“峰回路转,柳暗花明又一村”,从而启发人们采用分段插值;而在飞机机翼的设计及精密器械的加工等发面,对函数曲线的光滑性要求比较高,分段三次埃尔米特插值不能满足光滑性需求,自然而然引出了三次样条插值。这是一个层层递进的过程,向学生阐释了学习不应该停留在知识的表面,要勇于发现新知识,敢于探索研究。
利用数值积分进行近似计算,必然要对其进行误差分析。在讨论求积公式的余项时,不是按照传统的教学内容逐个去推导分析,根据代数精度的概念,设求积公式
从而得到所需求积公式的余项,也可将其应用到高精度的高斯型求积公式中。这就是化归的策略,不是对问题进行正面的“攻击”,而是不断将问题加工变形,探究其内在本质,让学生养成良好的思考意识。
在教学中,合理的优化教学内容,丰富学生的数学知识,活跃学生的思想,使学生具有强烈的参与意识,能在经典算法的启示下,构造出新的算法, 引导学生创新思维的培养。
(五) 在实际教学中引入 Matlab 软件,培养学生的实操能力
我在数值分析课程教学中引用 Matlab 软件,该软件既有良好的数值计算功能,又具备强大的图像处理功能,同时用户界面也简单易懂,学习者能够在短时间内掌握这个软件的丰富功能。由于数值分析课程体系的特点,应用传统教学方法很难将课程精髓展现给学生,也不能提起学生的学习兴趣,教学效果不是很理想,长此以往,很多学生因枯燥的教学氛围慢慢产生了消极的学习情绪。
针对此现象, 在授课中,借助 Matlab 软件引导学生用“数值分析” 中的插值、拟合、逼近等方法处理实际生活中的数据, 如:人口数据分析、新冠病例数据分析、股票趋势分析等等,通过实例演示教学,让学生看到数值分析课程在实际生活中的应用,对“数值分析”课程逐渐产生学习兴趣 [6-7]。
运用 Matlab 数值实验,一方面使教学方式方法得到丰富,使课程教学多样化;另一方面,提高数值分析课程的可视化效果。从而深化学生对该课程理论知识的直观理解和解释解决现实问题的能力。例如,在学习了前面几种插值法之后,学生会发现随着多项式次数的增高,插值函数逼近的效果会越来越好,其实这只是一个假象。例如,函数学生可通过 Matlab 程序的可视化图形观察到高次多项式插值的 Runge 现象,进而理解高次多项式插值的病态,这不仅让学生深刻理解了该部分相对比较抽象的知识内容,也展示出数学的迷惑性和魅力。通过这种授课形式引发了学生学习和利用数学知识解决实际问题的兴趣。
数值实验是数值分析课程教学中的一个重要环节,通过数值实验将数值分析课程中的理论知识与实际应用相结合,充分展示其实际应用的广泛性和重要性。Matlab 软件就是数值分析课程数值实验的一个载体,利用 Matlab 软件对教学中的实例求解过程再进行演示,引导学生尝试一题多解,拓展思维和现实应用。
例如,在线性方程组的迭代解法中,针对具体的问题,运用 Matlab 程序,比较雅克比迭代、高斯赛德尔迭代、超松弛迭代的敛散性及收敛速度,进行优劣分析。通过图形、数表等方式对同一问题的几种数值算法结果进行比对,给学生从理论到几何直观展示不同算法在求解过程中的误差大小和收敛速度等,学生也能够直观地筛选出最优算法 [8]。
在实际教学中强化数值实验和程序设计环节, 使学生熟练掌握常用数值算法的构造原理、过程分析,提高对数值分析课程中算法思想、理论分析的理解以及应用。培养学生将现实问题转化为数学模型,构造合理的数值计算方法,利用 Matlab 程序得出结果,再分析模型与实际问题的锲合度,对数学模型进行修正,提高锲合度。通过这样的实践教学, 提高学生学习的积极性,激发学生潜在的创新意识。
通过数值分析课程中的数值实验教学环节,不仅加深了学生对数值分析课程理论知识的掌握,而且培养了学生实际动手能力,达到学以致用的目的, 提高了学生分析问题和解决问题的能力,培养了学生的创新能力。同时,提升了学生数学素养,为学生将来更好地适应工作和科研环境打下良好的基础。
四 结语
在当前新时代新形势的背景下,数值分析的教学改革和实践工作需要我们不断地探索和创新。我校在数值分析课程的教学中采取一系列创新和改革后,学生对该课程的学习积极性和兴趣大大增强。在实际教学过程中,学生参与意识、独立思考和创新思维能力明显增强,课后作业、课程考核成效也大为改善。
教与学相得益彰,数值分析创新型培养模式也为其他数学课程的教学改革提供了经验。当然,我们应当在教学中不断提高学生的创新能力,真正实现新时代需求的高素质复合型人才的培养目标。
参考文献
[1]李庆扬,王能超,易大义,编 . 数值分析 ( 第五版 )[M]. 北京 : 清华大学出版社 ,2008.
[2]刘三明 .《数值分析》课程中应用“翻转课堂”教学模式的探讨 [J]. 教育教学论坛,2018(6):179-181.
[3]耿爱成,史书慧 . 工程硕士课程“数值分析”教学改革研究 [J]. 沈阳师范大学学报(自然科学版),2017,(35):494-497.
[4]王海军,陈兴同,杨然 . 基于问题与能力培养的《数值分析》课程教学改革与实践探究 [J]. 高教论坛,2020,(2):43-45.
[5]闵杰,李璐,欧剑 .《数值分析》课程思政教学改革研究与实践 [J]. 大学数学,2020,(36):40-45.
[6]秦厚荣,徐海蓉.大学数学课程思政的“触点”和教学体系建设 [J]. 中国大学教学,2019,(9):61-64.
[7]李俊玲,安玉莲 .“数值分析”课程教学改革的思考与建议 [J]. 教育现代化,2019,(24):62-64.
[8]聂存云,陈晓玲,杨继明,等 .“问题驱动式”教学法在“数值分析”课程教学中的应用与研究 [J]. 湖南工程学院学报, 2016(6):100-104.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/32378.html