SCI论文(www.lunwensci.com):
摘要:平面向量的坐标表示,在本模块知识体系中,不管知识还是方法都起着承上启下的重要作用。充分把握好这部分内容可以很好的梳理向量相关概念,也可以为后面向量的坐标运算及向量内积打下良好的基础。文章从一个例子的解法具体展开,分析其解题思路,并挖掘其价值和意义。
关键词:平面向量;思维;数形结合
本文引用格式:陈九香.例说平面向量的坐标表示[J].教育现代化,2019,6(28):247-248.
平面向量的原型是生活中无处不在的力,平面向量知识在物理、数学等诸多分支中均有着非常广泛的应用。它具有几何与代数的“双重身份”,可以将数和形有机融合,也可以综合数学诸多主干知识。从教材结构分析,平面向量的坐标表示处于正中间,学习向量的坐标表示,重点在于串联前后知识,学会综合运用,熟练数与形的分析方法,提升思维的深刻性、广阔性和灵活性。
一 平面向量的坐标表示“示例”
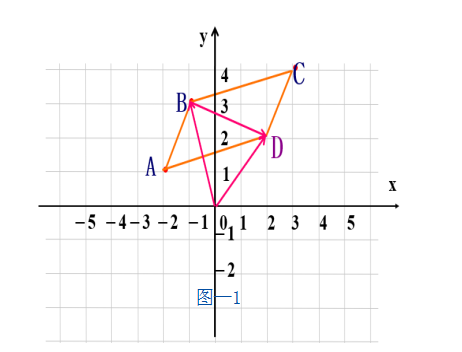
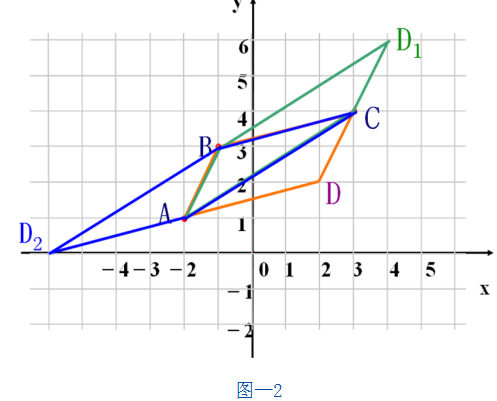
例:已知 的三个顶点A、B、C的坐标分别是(-2,1),(-1,3),(3,4),求顶点D的坐标。分析:作图可知点D的坐标有三个(如图—1)。因为求解方法相似,所以本题重点是围绕其中一个答案的求解进行深入的剖析。前面学习了平面向量基本概念及加减法。若能充分运用所学知识进行灵活运用,本题求解方法可以非常多样。具体求解如下(参看图-2)。

 二 巧用图形分析,产生直观效果
二 巧用图形分析,产生直观效果
平面向量是数形结合的良好载体。向量的有向线段表示法,向量加减法的两个法则,都是向量坐标表示用图形辅助解决问题的基础,结合图形分析使得问题解决更加高效。
本例中,把直角坐标系建立在网格线中调动观察者的直觉思维,稍加观察便能大概知道第四个点的大概位置。为了知识的全面掌握和多方法解题,就需要费一番心思结合图形提出一系列问题,从而推动思考不断深入探索。
问题分解说解法。(1)如图三个顶点,你认为第四个顶点大概在什么位置?(2)假设点D在点C左下方,请仔细观察,试试能画出哪些向量来?(3)这些向量之间有什么关系吗?能否用加法法则联系起来?(4)运用关系和法则时方法唯一吗?
数借助形产生直观效果,形借助数才能深刻入微。因为有了图形的直观效果,顺着这些问题的不断推进,自然而然的运用向量概念及加法两个法则顺利求解。循着以上问题,由浅入深层层递进一步一步接近问题的本质。将思考过程分解成了很多个学生易于解决的小问题,从而化难为易,也更好的打开了解题思路,使解题方法更加灵活多样。通过数形结合曲径通幽不断深入,不断产生新的发现,既增强了解决问题的趣味性,也增强了解题的成就感。
三 利用解题过程提升思维的深刻性、广阔性和灵活性
数学思维品质:是指学生在数学学习过程中的思维习惯及方式的个性化表现形式。它体现了个体思维水平和能力的差异,是衡量数学思维优劣、判断数学能力高低的主要指标。循着上述问题多种方法解决本例,能很好的提升思维的深刻性、广阔性和灵活性。
(一)提升思维的深刻性
思维的深刻性是指思维活动的抽象程度和逻辑水平,以及思维活动的深度和难度。它表现在能深入的专研与思考问题,理解问题深刻透彻,推理严密逻辑性强,并能解决难度较大的问题。必须善于抓住问题的本质和规律,仔细分析并找出问题中条件与结论之间的联系而不被表象所迷惑。解题之后能总结规律和方法,做到举一反三,把获得的知识的方法迁移运用于解决类似问题,这样才能将方法内化为能力,提升解决问题的综合水平。
能迅速看到并表达出问题本质的学生并不多,因此数学思维深刻性品质的培养是一项艰巨的工程。本例通过问题分解说解法,揭示了知识发生发展的过程,对问题情境中的隐含条件进行了深入的挖掘,使得一团乱麻的思绪得到了梳理。同时寻到了一种普遍使用的方法,在解决一些较难较大的问题时,都可以将问题进行分解,实现了方法的迁移能力的内化。
(二)提升思维的广阔性
思维的广阔性是指思维活动作用范围的广泛和全面程度。它是指能全面地看问题、思路开阔、多角度探求。在思维活动中,它的表现是既注意把握事物的整体,又不忽视重要的细节,能够从广阔的层面上捕捉有效的信息,广泛对比和联想,从而一题多解或一法多用。
本例求解过程中,需要整体把握各知识点间的联系,灵活整合以深入挖掘并拓展思路,建立前后各知识点的横向及纵向联系,从而多角度、多方位探求得出多种解法。本例用到了向量的线段表示法,向量相等的概念,向量加法的两个法则,向量的坐标表示,知识跨度较大综合性强。找出了一个D点坐标之后,另外两个方位的D点坐标求解,也是需要观察和思考周全的。培养思维的广阔性,建立在对某模块各概念的深刻理解基础上。
(三)提升思维的灵活性
思维灵活性是指能从不同的角度、不同的方面采取灵活多样的方法来思考问题。善于根据情况的变化,及时调整原来的思维过程与方法,不囿于固定模式,具有较强的应变能力。思维灵活性是多方面的。首先,分析问题着手点灵活,能从不同角度、方向分析问题,多种途径解题;其次,思维过程灵活,能从分析到综合,也能从综合到分析,思维方法的运用转换灵活;再次,对数学方法的运用灵活,善于进行分析、类比、联想,同时根据具体问题进行自我调节,具有思维的应变能力;最后,正向思维的同时,也善于进行逆向思维的思考。
参考文献
[1]龙敏信.数学思维的特点[J].数学教育学报,1992(12):56.
[2]曹亚东.平面向量问题的切入点探究[J].中学数学研究,2018(9):39-40.
[3]章水云,叶兴炎.平面向量:数的外表、形的内涵[J].中学教研(数学),2014(10):47-50.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/9379.html