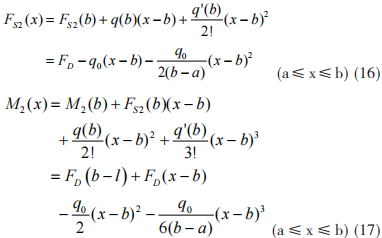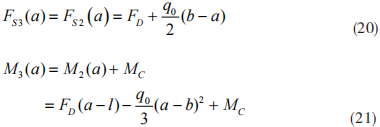SCI论文(www.lunwensci.com):
摘 要:梁的弯曲内力是“材料力学”课程中学生必须熟练掌握的一个知识要点。计算梁弯曲变形时的剪力和弯矩是对梁进行强度分析和刚度分析的一个重要步骤。本文通过对剪力和弯矩函数进行泰勒级数展开来确定剪力和弯矩方程,为计算梁弯曲内力提供了一种新的思路和方法。对于均布、线性以及 n 次分布载荷作用的梁,通过该方法均可得到准确的剪力和弯矩方程表达。结合实例,详细阐述了在梁受较复杂载荷作用下应用此方法确定弯曲内力的计算过程,并总结了此方法特征。该方法作为计算弯曲内力的一种创新方法,可作为“材料力学”课堂教学的扩展内容,有助于学生创新意识和知识应用能力的培养。
关键词:剪力;弯矩;泰勒级数;多项式;载荷集度;材料力学
本文引用格式:夏冬生 , 朱公志 , 孙先念 , 等 .“材料力学”课程中确定梁弯曲内力的一种新方法探究 [J]. 教育现代化 ,2020,7(97):133-136
A New Method to Determine the Bending Internal Force of Beams in the Course of "Mechanics of Materials"
XIA Dongsheng1, ZHU Gongzhi1, SUN Xiannian1, Yao Zheng1, YU Yan2, Liu Yang1
(1. College of Transportation Engineering, Dalian Maritime University, Dalian Liaoning; 2. Naval Architecture and Ocean Engineering College, Dalian Maritime University, Dalian Liaoning)
Abstract: Determination of the bending internal forces of beam is a key point that students must master in the course of Material Mechanics. Calculation of bending internal forces is an important step to analyze the strength and rigidity of a beam. It is explored to determine the shearing force and bending moment equations with the method of Taylor series expansion in this paper, which provides a new idea for determining the bending internal forces. For a beam subjected to an uniform, linear or nth power distributed load, the exact expressions of shearing force equation and bending moment equation can be obtained by this new method. Combined with several examples, the detailed calculation processes of the bending internal forces by this new method for a beam subjected to different loads are given. Finally, the characteristics of this method are concluded. This innovative method to determine the bending internal forces can be introduced in the course of Material Mechanics as an extended knowledge. It is helpful to enhance the awareness of innovation and the abilities of applying knowledge for students.
Key words: shearing force; bending moment; Taylor series; polynomial; distributed load density; material mechanics
一 引言
“材料力学”是工科类专业一门较重要的专业基础课程,是大学生最先接触到与工程实际密切相关的课程。材料力学紧密结合工程实际中的力学问题, 通过理论、实验和计算,解决构件受力后的强度、刚度和稳定性问题,为工程设计提供理论基础和计算方法,达到工程应用中经济性和安全性平衡的目的。通过“材料力学”的学习,要求学生能够运用材料力学的理论和方法分析、解决一些简单的工程实际问题。“材料力学”课程具有基础理论和工程应用的双重性,使其非常适于培养和提高学生科学素质和科技创新能力。
在“材料力学”中,画构件内力图是对构件进行强度分析和刚度分析的一个重要步骤。内力图可直观表示截面内力沿轴线的变化趋势,易于判定构件的危险截面。弯曲变形是工程中构件发生的主要变形之一。相对轴向拉压变形的轴力图和扭转变形的扭矩图,画梁弯曲的剪力图和弯矩图较复杂和繁琐。因此画梁的剪力和弯矩图一直是材料力学教学的一个重点和难点 [1-3]。
确定梁的剪力和弯矩的主要方法有截面法、微分积分关系法、奇异函数法和叠加法等。截面法是求弯曲内力的基础方法。但在复杂载荷作用下,由于需多次截取截面,对多个梁段受力分析、建立平衡方程并计算,该方法的计算量冗长 [4,5]。微分积分关系法利用载荷集度、剪力和弯矩三者的微分和积分关系结合计算特殊截面的弯曲内力,可快速画出梁的剪力和弯矩图 [1,2]。叠加法则是把复杂载荷分解为各典型简单载荷,然后将各简单载荷单独作用的内力图相叠加的方法 [6]。叠加法对于受复杂载荷作用的超静定梁较适用。奇异函数法是利用奇异函数在处理非连续性问题时不需要分段计算的特性,将梁上分布载荷集度用奇异函数的形式统一表达,通过对奇异函数积分可得到由一个方程统一表达的弯曲内力 [7]。奇异函数法使计算表达式得以简化,而且计算步骤程式化,有利于通过编程来计算弯曲内力 [8]。
由于剪力和弯矩方程均是截面位置 x 的函数, 且一般表示为 x 的 n 次多项式, 所以本文尝试通过对剪力和弯矩函数进行泰勒级数 (Taylor series) 展开的方法确定梁弯曲剪力和弯矩方程,为梁弯曲内力计算提供一种新思路。
二 弯曲内力的泰勒级数展开式
数学中,如果函数足够平滑,且已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。
由于承弯构件因支承结构和载荷类型多样,剪力 FS(x) 和弯矩 M(x) 方程往往是分段函数。对于某一梁段,若剪力和弯矩函数在该区间 [a,b] 有 n 阶导数,且在开区间 (a,b) 上具有 (n+1) 阶导数,则可对剪力和弯矩函数在该梁段内某处应用泰勒级数展开,得到
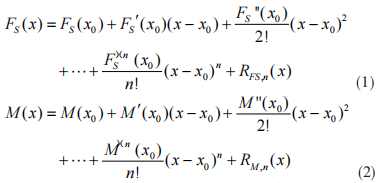
上式中,RFS,n(x) 和 RM,n(x) 分别为剪力和弯矩函数的泰勒级数展开式的余项。
材料力学中已推导弯矩、剪力和载荷集度三者具有如下关系 [1-2]
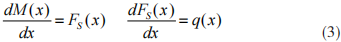
将 (3) 式分别代入上式 (1) 和 (2),得到
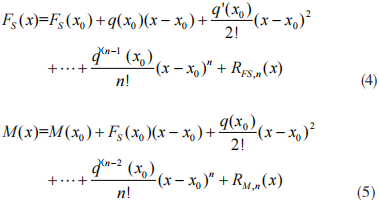
考虑载荷集度 q(x) 一般为 x 的 m 次方函数的情况,则剪力 FS(x) 和弯矩 M(x) 函数的泰勒级数展开式为
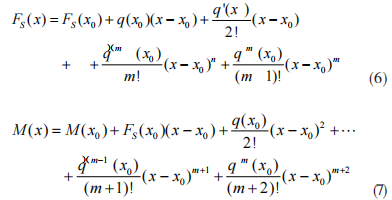
由于载荷集度 q(x) 的高于 m 阶导数均为零,上式 (6) 和 (7) 的余项误差为 0, 所以应用泰勒级数展开所得到 (x-x0) 的 m+1 和 m+2 次多项式是此梁段弯曲内力的准确表达。通过该方法得到的 (x-x0) 多项式,其各项系数为剪力和弯矩函数在 x0 处的各阶导数。应用此方法,一般应选择梁段内特殊处 ( 一般为端点 ) 进行泰勒级数展开,目的是为了剪力和弯矩函数在该处各阶导数易直接确定。
三 算 例
例 1 图 1 所示一简支梁受抛物线型载荷集度
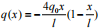
( 方向向下为负 ) 的作用,求该梁的剪( 方向向下为负 ) 的作用,求该梁的剪
解 以梁为研究对象,通过列静力学平衡方FS(0)=FA,M(0)=0。将剪力和弯矩函数在 A 处进行泰勒级数展开,得到
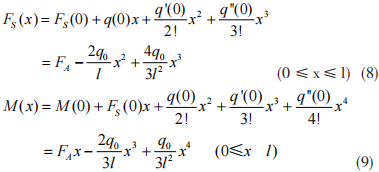
例 2 图 2 所示一简支梁受梯形分布载荷集度
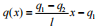
和一集中载荷 FB 作用,求该梁的剪力和弯矩方程。
解 以简支梁为研究对象,通过列平衡方程,可分别求出两端支反力 FA 和 FC。该梁的剪力和弯矩方程是分段函数。
AB 梁段 A 截面内力为 FS1(0)=FA,M1(0)=0。在 A 处对该梁段的剪力和弯矩函数进行泰勒级数展开,得到

BC 梁段 C 截面内力为 FS2(0)=-FC,M2(0)=0。在 C 处对该梁段的剪力和弯矩函数进行泰勒级数展开,得到
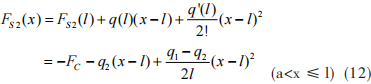

例 3 图示一悬臂梁受三角形载荷集度
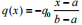
(a ≤ x ≤ b)、一集中力偶 MC 和载荷 FD作用,求该梁的剪力和弯矩方程。
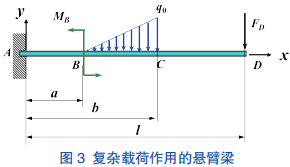
对于悬臂梁,不必求固定端处约束反力。该梁的剪力和弯矩方程是分段函数。
CD 梁段 D 截面内力为 FS1(0)=FD,M1(0)=0。在 D 处对该梁段的剪力和弯矩函数进行泰勒级数展开,得到

由 (14) 和 (15) 式,可确定 C 截面弯曲内力为FS1(b)=FD,M1(b)=FD(b-l)。
BC 梁 段 C 截 面 内 力 为 FS2(b)=FS1(b)=FD, M2(b)=M1(b)=FD(b-l)。在 C 处对该梁段的剪力和弯矩函数进行泰勒级数展开,得到
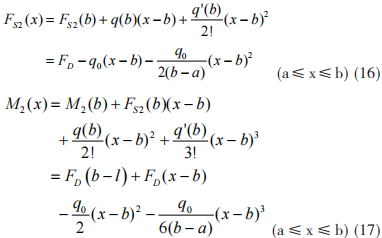
由 (16) 和 (17) 式可确定 B+ 截面的弯曲内力为

AB 梁段 B- 截面的弯曲内力为
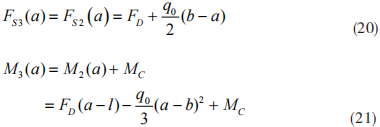
在 B 处对该梁段的剪力和弯矩函数进行泰勒级数展开,得到
 四 结语
四 结语
(1)一般将某梁段的剪力、弯矩函数在梁段的一端处进行泰勒级数展开,多项式中各系数为该处的各阶导数,易直接确定。
(2)不论是静定梁还是超静定梁,该方法具有普遍性,特别是复杂分布载荷作用下静定梁的求解具有优势。应用此方法可推广求解其他材料力学问题, 例如计算梁弯曲变形。
(3)计算步骤程式化,适于通过编程计算各梁段的弯曲内力。
(4)本文提出的计算弯曲内力的新方法可作为材料力学课程的知识拓展内容引入教学中,有助于学生创新意识和知识应用能力的培养。
参考文献
[1]徐志军 , 原方 . 建筑专业建筑力学课程中弯曲内力的教学方法探讨 [J]. 大学教育 ,2019(5):88-90.
[2]朱伊德 . 计算梁弯曲变形和内力的简易方法 [J]. 力学与实践 ,2013,35(2):88-90.
[3]陈俊旗 , 白杨 , 咸庆军 . 有限单元法在弯曲内力和弯曲应力教学中的应用 [J]. 河南教育 ( 高教 ),2018(4):84-86.
[4]刘洪文 . 材料力学 ( 第 6 版 )[M]. 北京 : 高等教育出版社 ,2017.
[5]单辉祖 . 材料力学 ( 第 3 版 )[M]. 北京 : 高等教育出版社 ,2009.
[6]周臻 , 尹凌峰 , 缪志伟 . 静定刚架弯矩图的叠加法活用与对称性利用 [J]. 力学与实践 ,2012,34(4):73-75.
[7]朱骥 . 奇异函数在材料力学中的应用 [J]. 纺织高校基础科学学报 ,1998,11(2):23-28.
[8]艾敏 . 奇异函数在材料力学计算机分析中的应用 [J]. 力学与实践 ,1989(6):56-59.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/32130.html

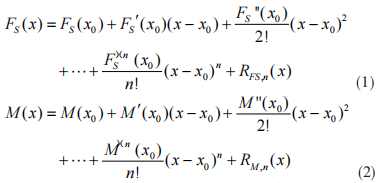
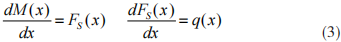
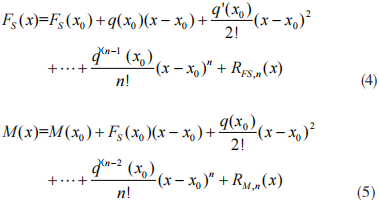
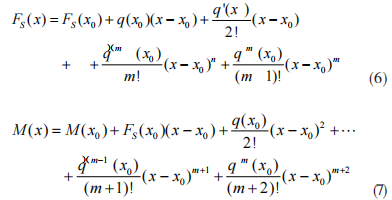
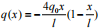 ( 方向向下为负 ) 的作用,求该梁的剪( 方向向下为负 ) 的作用,求该梁的剪
( 方向向下为负 ) 的作用,求该梁的剪( 方向向下为负 ) 的作用,求该梁的剪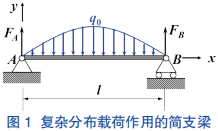
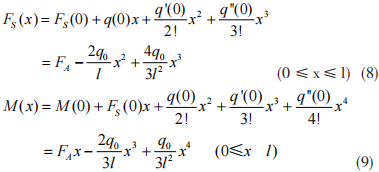
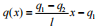 和一集中载荷 FB 作用,求该梁的剪力和弯矩方程。
和一集中载荷 FB 作用,求该梁的剪力和弯矩方程。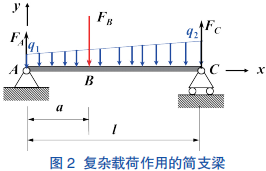

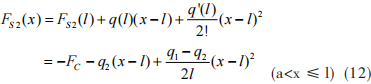

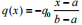 (a ≤ x ≤ b)、一集中力偶 MC 和载荷 FD作用,求该梁的剪力和弯矩方程。
(a ≤ x ≤ b)、一集中力偶 MC 和载荷 FD作用,求该梁的剪力和弯矩方程。