SCI论文(www.lunwensci.com):
摘要:Matlab是一款支持程序设计的数学软件,越来越多的理工、经管类专业开设了相关课程。针对当前Matlab课程教学中偏重命令格式、语法规则等理论知识,学生学习兴趣不高的问题,本文以Matlab中多项式数据拟合教学内容为例探讨了案例式教学设计,对提高学生应用Matlab程序设计解决实际问题的能力取得了良好效果。
关键词:Matlab教学;多项式数据拟合;案例式教学
本文引用格式:杨炼,等.Matlab多项式数据拟合的案例式教学设计[J].教育现代化,2019,6(09):93-95.
一引言
Matlab是由美国MathWorks公司于1984年推出的一款支持程序设计的数学软件[1]。该软件执行程序员的工作有两种方式,分别是命令方式和程序方式,目前已经涵盖了数理统计、偏微分方程、数据处理与分析、仿真系统、最优化计算、神经网络等当今绝大多数应用领域,以其编程效率高、用户使用方便、语言简单以及绘图功能丰富等特点受到广大工程技术人员及科研工作者的欢迎。同时《Matlab程序设计》及类似的课程也成为了各高校理工、经管类专业的必修课程或选修课程。此外,越来越多的课程教学都引入了Matlab进行辅助教学[2-7]。但目前在国内,如果学生将Matlab语言作为纯粹的一门计算机语言进行学习,那么该课程需要掌握的指令及编程技巧非常繁杂,也就是入门容易精通困难,应用能力差[8],学习兴趣不是很高。此外,当前高校的Matlab教学偏重命令格式、语法规则等理论知识,对培养和提高学生解决实际问题的能力还不够重视[9]。为此,笔者在多年的教学基础上,将生产、生活中存在的实际问题设计成教学案例并引入到Matlab教学过程中来,采用案例教学法,培养学生利用Matlab解决实际问题的能力,有效激发了学生的学习兴趣,获得了较好的教学效果[9,10]。案例教学是以学生为中心,以案例为基本教学内容,以师生互动为基础,通过呈现案例情境,将理论与实践紧密结合,引导学生发现问题、分析问题、解决问题,从而掌握理论、形成观点、提高能力的一种开放、启发式教学方式[11]。其本质是理论与实践相结合的互动教学模式,代表未来教育方向的成功教育模式[12,13]。文献[14]利用Matlab软件的模拟仿真功能,就三个典型的光学问题进行案例式讨论,让学生接触直观的实验现象,正确地理解光学概念。文献[15]针对电机学课程基本概念抽象,公式推导繁琐,学生难以理解的问题,将Matlab仿真技术应用于电机学教学过程中,通过变压器3个仿真案例,说明了该方法能够将抽象问题形象化、直观化,有利于调动学生的学习积极性,提高了教学质量和效果。文献[16]阐述了Matlab课程教学现状以及案例互动式教学在Matlab课程中的设计应用,实践教学表明,案例互动式教学模式能有效提高教学效果。本文以Matlab中多项式数据拟合为例探讨案例式教学。
二 Matlab多项式数据拟合的新课导入
曲线拟合是曲线逼近最常见的一种形式,是数学研究中一种利用解析表达式逼近已知离散数据的方法。由于曲线拟合只要求拟合的曲线能大致模拟数据的基本趋势故而有多种判别准则,如使偏差的绝对值之和最小,使偏差的最大绝对值最小和使偏差的平方和最小(最小二乘法)。一般都采用最小二乘法来确定多项式的系数。
数据拟合教学内容的引入:已知平面上n个采样点,其横坐标和纵坐标分别构成两个行向量Xi和Yi,其中i=1,…n,通过构造一个函数fun,使得在误差最小的情况下,函数曲线最接近这些采样点。为便于计算,数据拟合的函数需要用一个相对简单的函数去逼近采样点,因此Matlab采用了多项式函数,常用的使用形式为[P,S]=polyfit(X,Y,m),该函数将根据X向量和Y向量及指定的多项式此时m来确定系数向量P,S为采样点的误差向量。得到用于拟合的多项式后,该多项式便可进行数据拟合或预测。
Matlab提供了一个函数polyval来计算拟合函数值,具体使用形式为y=polyval(P,x),利用采样点横坐标x向前计算便可实现预测。
三教学案例设计
(一)案例题干与分析
天猫“双十一”购物节始于2009年,以天猫、京东、苏宁易购为代表的大型电子商务网站一般会利用这一天来进行一些大规模的打折促销活动,以提高销售额度,逐渐成为中国互联网最大规模的商业促销狂欢活动。由于天猫“双十一”的影响力逐渐增大,围绕每年天猫“双十一”的销售额的预测也成为了国内外各大资讯公司和金融机构的关注热点。事实上,天猫“双十一”销售额的预测完全可以利用Matlab多项式拟合来完成,而且预测结果与实际情况基本吻合。因此,作者在讲授多项式拟合时设计了对天猫“双十一”销售额预测的教学案例。案例题干如下:
通过网络查阅历年天猫“双十一”销售额,求解如下实际问题:
1)利用2009年到2017年销售额数据并进行2次多项式函数拟合,预测2016年和2017的天猫双十一的销售额(取整)及预测的误差(误差用百分比表示,精确到小数点4位)
2)国内外的一些资讯公司和金融机构的数据分析师预测2017年的天猫销售额将达1520亿元,理由是天猫双十一销售额的高速增长率将放缓而出现拐点,事实证明时候未到,如果2017年的销售额就是1520亿元,求出2009-2017年销售额的3次多项式拟合函数及未来15年内的最大值(精确到小数点1位)。
案例分析:该案例没有直接给出历年天猫“双十一”的销售额具体数据,在实践教学时要求学生在实验室电脑上进行网络搜索,培养了学生实践动手能力。预测2017年的销售额时,可利用2009年到2016年的销售额数据,而预测2016年的销售额时,则已知的数据只能用到2015年的。如果每年的销售额呈中高速增长态势,则可用2次多项式进行拟合,这的确也符合2017年的实际情况,但从长远来看不可能一直维持着中高速增长率。为此,在设计本案例时,新增了第二个问题,即如果销售额增长率放缓而出现拐点,则多项式拟合时至少需要3次。
(二)案例解答
通过网络搜索可以得到从2009年到2017年的实际销售额数据为[0.52 9.36 52 191 350 571 912
1207 1682],单位是亿元人民币。该案例既要求学生熟练掌握Matlab多项式拟合方法,同时也巩固了之前所学的极值问题求解方法。编写Matlab代码如下,
问题1的代码:
y=[0.52 9.36 52 191 350 571 912 1207
1682];
len=length(y);
k=polyfit(1:len-2,y(1:len-2),2);y2016=fix(polyval(k,len-1));
disp([‘预测2016年销售额是’num2str(y2016)‘亿元’])
err=abs(y2016-y(len-1))/y(len-1)*100;disp([‘预测误差是’num2str(err)‘%’])
k=polyfit(1:len-1,y(1:len-1),2);y2017=fix(polyval(k,len));
disp([‘预测2017年销售额是’num2str(y2017)‘亿元’])
err=abs(y2017-y(len))/y(len)*100;disp([‘预测误差是’num2str(err)‘%’])结果:
预测2016年销售额是1262亿元
预测误差是4.5568%
预测2017年销售额是1626亿元
预测误差是3.3294%
问题2的代码:
y=[0.52 9.36 52 191 350 571 912 1207 1520];n=3;
k=-polyfit(1:length(y),y,n);if n==3
s=[num2str(k(1))‘*x^3+’num2str(k(2))
‘*x^2+’num2str(k(3))‘*x+’…
num2str(k(4))];end
f=inline(s);
[x min]=fminbnd(f,8,30);max=-min
结果是:4407.2
(三)案例引申思考
案例解答后,可以对学生进行延伸思考,首先从问题一的结果来看,利用多项式拟合的方法得到的预测结果精度都很高,说明了方法的可靠性,那么可以要学生对今年即将到来的“双十一”销售额进行预测,并思考方法上是否需要完善或修改。另外,将给定的采样点与拟合后的函数值进行绘图,并进行拟合效果的对比。
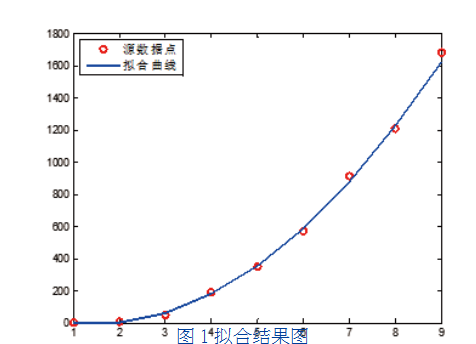
利用Matlab绘图进行对比的代码如下:G=plot(1:9,yf,’b-’,1:9,y,’ro’);set(G,’LineWidth’,2.5)绘制结果如图1所示,其中拟合曲线用2.5磅大小的蓝色实线表示,采样的数据点用红色圆圈表示,从实际效果来看,拟合的误差较低。
从拟合结果图中可以看出,利用2次多项式函数对2009年到2017年的天猫“双十一”销售额拟合的数据与实际数据还是非常吻合的,可适用于预测。
四 结语
本文针对Matlab教学中多项式数据拟合教学内容设计了一个与现实生活密切相关的教学案例。通过案例式教学一方面便于学生理解所学的新内容,另一方面通过精心设计的案例把新内容和以及学过的内容综合起来,可以提高学生的独立思考能力,加深学生对一些重要函数的理解及实际运用。经过连续三年的教学实践,案例式教学能够很好的培养学生学习Matlab程序设计的兴趣,避免了陷入传统编程语言教学的困境,取得了良好的教学效果。
参考文献
[1]贺跃帮,王天雷,李兴春,等.基于案例的MATLAB教学探讨与实践[J].科技创新导报,2017,14(13):226-228.
[2]徐富强,陶有田.金融Matlab仿真教学案例设计[J].安庆师范学院学报(自然科学版),2016,22(04):149-151
[3]陈文凯,贺建良,黄娟.基于MATLAB的《机械工程控制基础》案例教学[J].湖南农机,2014,41(08):94-96.
[4]万凯,卢莎.基于MATLAB仿真的《高频电路》教学探讨[J].现代计算机(专业版),2018(04):60-62.
[5]谢自梅,范黎林.基于MATLAB的促进师生共同发展的《信号与系统》课程教学改革[J].教育教学论坛,2018(11):103-104.
[6]何江芸.Matlab在高校线性规划教学中的编程应用研究[J].教育教学论坛,2018(10):181-184.
[7]唐斌,伍振海.Matlab在大学物理教学中的应用研究[J].教育教学论坛,2017(46):270-271.
[8]张玉叶.Matlab语言课程教学中若干问题探讨[J].实验室研究与探索,2018,37(03):176-179.
[9]杨炼,李军成,刘成志.应用型本科《Matlab程序设计》案例式教学改革[J].南方农机,2018,49(21):12-13.
[10]贺跃帮,王天雷,李兴春,等.基于案例的MATLAB教学探讨与实践[J].科技创新导报,2017,14(13):226-228.
[11]赵兰英,薛冬娟,于靖博,等.案例教学在MATLAB与仿真技术课程中的应用探讨[J].装备制造技术,2016(12):227-229.
[12]刘刚.哈佛商学院案例教学作用机制及其启示[J].中国高教研究,2008(5):89-91.
[13]张家军,靳玉乐.论案例教学的本质与特点[J].中国教育学刊,2004(1):48-62.
[14]薛海国.MATLAB在光学习题课教学中的应用[J].教育现代化,2018,5(33):207-209.
[15]张绍彪,王定友,陶俊斌.Matlab仿真在电机学教学中的应用[J].教育现代化,2018,5(27):195-196.
[16]曾玖贞,王超.新工科背景下运用互动式教学模式提高Matlab教学效果[J].教育现代化,2018,5(23):268-269.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/7842.html