SCI论文(www.lunwensci.com):
摘要:《普通高中数学课程标准(2017年版)》(以下简称课标)明确指出将数学文化融入课程内容;2017年出台的普通高等学校招生统一考试大纲(理科数学)将数学文化列入高考内容;2018年数学高考全国卷中也适当融入数学文化。可见,数学文化在数学教育界越来越受重视。本文将对2018年数学全国卷中出现的融入数学文化的高考题进行分析,并提出相关的看法和建议。
关键词:数学文化;高考题;课程标准
本文引用格式:袁弘,等.浅析高考题中的数学文化融入[J].教育现代化,2019,6(69):171-172.
一 引言
数学是一种文化现象[1],那么何为数学文化?课标指出“数学文化是指数学的思想、精神、语言、方法、观点以及它们的形成和发展;还包括数学在人类生活、科学技术、社会发展中的贡献和意义,以及与数学相关的人文活动[2]”,数学文化不仅体现出数学的人文价值,更体现了数学的科学价值。数学学科具有高度的抽象性和逻辑的严谨性,学生在学习时经常会出现“数学太难”“对数学不感兴趣”等情况,融入数学文化有利于学生更好地理解数学的本质,帮助学生建构数学知识体系;融入数学文化有助于提高学生的数学核心素养,课标强调数学学科核心素养,而核心素养的培养也离不开数学文化,教师在教育教学过程中要将数学知识的文化背景与知识点本身结合起来,为学生提供多方向、多角度地思考和解决问题;融入数学文化有助于激发学生的求知欲和探索创新精神,数学这门科学在历史的进程中充满了矛盾与猜想,适当地引入数学史、数学名著、数学名题、数学美和数学与科技等数学文化对于激发学生的求知欲和拓展学生的思维水平具有重要意义。
因此,数学文化越来越被人们所重视,数学高考题中有关数学文化的题目也越来越多,本文以2018年数学全国卷I、II中的两道高考题为例,通过对其呈现方式、考察形式、渗透数学文化的自然性等的分析,谈谈高考题中的数学文化融入。
二2018高考试题中数学文化分析
课标已将“体现数学的文化价值”作为高中数学课程的基本理念之一,并且明确要求数学课程应适当反映数学历史、应用及发展趋势,帮助学生了解数学在人类文明发展中的作用,形成正确的数学观。鉴于高考试题是对课标要求的具体体现和落实,故本文将对2018年数学高考全国卷中有关数学文化融入的例题进行分析,将数学文化的考察形式作为切入点,结合本题考查的数学学科知识点,探究数学文化融入的自然性与科学性,并立足于学生,针对题目融入数学文化提出相关建议。
在2018年的高考全国理科数学试卷中,数学文化出现了两次,借鉴汪晓勤的分类标准,将其呈现方式分为显性和隐性两种,显然,卷I、II的呈现方式皆为显性;而借鉴唐恒钧、张维忠、汪晓勤等学者的分类标准,将其分为数学史、数学美、数学名著、数学名题、数学与科技五类,则卷I、II的考察形式则均为数学史。
(一)2018全国卷I高考理科选择题第10题分析
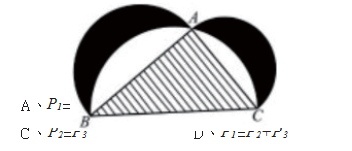
例1.(2018全国卷I高考理科选择题第10题)下图来自古希腊数学家波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB、AC,的三边所围成的区域记为I,黑色部分记为II,其余部分记为III,在整个图形中随机取一点,此点取自I、II、III的概率分别记为P1,P2,P3,则()
例1中通过引入古希腊数学家波克拉底,将他所研究的月牙几何图形与高中知识点几何概型结合起来,考察学生的灵活运用能力。当波克拉底研究月牙形时,人们还不知道如何科学地求圆的面积,但因为他的推动——将一个曲变形转化为一个直边形,极大地促进了圆的面积计算公式的问世,对于数学学科的发展有着巨大的影响。因此,在高考题中融入数学家波克拉底对于学生学习数学知识、体会数学中的科学和人文价值具有重要作用;此题考察的知识点为与面积有关的几何概型,其解题思路为设出每个半圆的半径,将区域I、II、III的面积分别用带有半径的式子表示出来,比较三个式子的大小。则通过解题方法我们可以看到本题具有很强的科学性和严谨性,但虽引入了数学文化,却在解题过程中忽略了对于数学文化本身的学习和探究,仅仅只是机械性地解题,更有甚者,为了更快地得到正确答案,在阅读本题题目时就会有所选择地放弃无关键信息的题干,这严重违背了考试大纲的初衷,因此,题目中融入数学文化的自然性有待提高,命题人要将数学文化的考察贯穿于学生解题的全过程,使得学生在解题学习中体会数学文化。
(二)2018全国卷II高考理科选择题第8题分析
例2.(2018全国卷II高考理科选择题第8题)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23,在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()
例2引入我国数学家陈景润在1966年证明了“哥德巴赫猜想”(它被称为是世界近代三大数学难题之一),即“任一充分大的偶数都可以表示成二个素数的和,或是一个素数和一个半素数的和”,将素数与高中知识点古典概型结合,考察学生的综合运用能力。本题不仅仅引入“哥德巴赫猜想”,而且是我国数学家关于此的发展和扩充,陈景润先生的这一贡献推动了数学科学不断向前发展。在本题中融入陈景润先生的证明有利于提高考生的爱国热情,增强考生的民族荣誉感。本题难度不大,但是在解题过程中需要学生从始至终明确“哥德巴赫猜想”的具体内容,根据其具体含义罗列出符合要求的素数,由古典概型定义得出正确答案。从渗透数学文化的自然性角度来看,本题很好地将二者融合在一起,有利于学生对于哥德巴赫猜想的深入探究,学生受到数学文化的感染和熏陶,自然而然就会对数学这门学科产生兴趣。
纵观近几年的高考数学试卷,数学文化的考察形式[3]包括数学史(如2013湖北卷理科第14题)、数学美(如2016四川卷文科第20题)、数学名著(如2015全国I卷文科第6题)、数学名题(如2013重庆卷理科第7题)、数学与科技(如2017北京卷理科第8题)等,大部分集中在数学史、数学名著和数学名题中,在数学美、数学与科技等方面的考察形式不够,且呈现方式大多为显性。按照如此趋势,往后的高考卷中数学文化的考察必不可少,且随着科学技术越来越被重视,数学文化在考察形式上将更偏重于数学与科技。
张奠宙先生曾提出数学欣赏[4],这意味着我们对待数学时不仅仅要将它看成一门严谨的科学,更要用欣赏的眼光将它看成一种美丽的文化。因此我们不仅要在考试中欣赏它,也要在教育教学过程中将它当作一种美丽的文化。而数学文化是多方面的,教学中渗透数学文化的方法也是多种多样的,但如何将数学文化与高考试题有机地结合在一起,仍是现在普遍学者正在思考和研究的问题。
纵观数学高考试题,命题中数学文化的渗透地位越来越重,但在考察形式上的多样性不够,仍有很大的发展空间。笔者提出相关建议,第一,新课标开设D、E类课程,包括对音乐、美术、体育、地方特色等的学习,则在命题时也可将音乐、美术、体育、地方特色与数学文化的融入相结合;第二,数学文化的渗透过程中要时刻注意学科本身的严谨性,特别是在数学史的融入方式上,应该加强这方面的研究;第三,高考中融入数学文化也离不开现实生活,故在命题中更要注意与日常生活的结合,注重数学知识的实际应用(反映在数学文化方面则为数学美的鉴赏、数学与科技的了解等);第四,高考中融入数学文化不可局限于选择、填空等客观题中,应更偏重于解答这类客观题,考生在进行开放性地解答时更容易阐述对数学文化的观点和理解,有利于将数学文化融入落到实处。
参考文献
[1]朱博.浅谈高考题中的数学文化渗透[J].数学学习与研究,2018(11):110.
[2]普通高中数学课程标准[M].2017.
[3]李春蕊,潘富格.析近5年高考中的数学文化试题[J].中学数学月刊,2018(09):52-54.
[4]张奠宙.谈课堂教学中如何进行数学欣赏[J].中学数学月刊,2010(10):1-3.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/28031.html