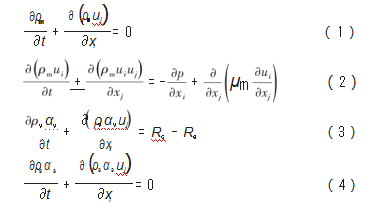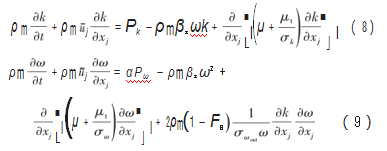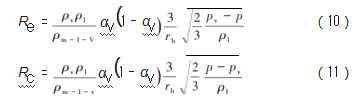摘要:为系统研究不同沙粒质量分数对离心泵内空化流动演化发展的影响,针对沙粒质量分数分别为1%、3%、5%与7%下的空化流动,采用SST k-ω湍流模型与Schnerr-Sauer空化模型,通过Fluent有限元软件,开展数值仿真,获取影响规律并揭示相应的机理。研究结果表明,随着沙粒质量分数从1%增加至7%,叶轮内空泡的分布范围持续变大,对应的空泡体积分数变高,临界空化余量与空化充分发展阶段的空化余量均不断变大。沙粒质量分数的增加显著促进离心泵内空化流动的发展。随着沙粒质量分数的增加,空化核子的数目不断增多,压力逐渐变小,湍动能持续增强,流线紊乱程度变强,在其综合影响下,沙粒显著促进空化流动在离心泵内的发展。且随着沙粒质量分数的增加,空化柔度值小于0的范围增加,空化柔度的振幅变化更加剧烈,稳定性整体减弱。
关键词:空化流动,沙粒质量分数,离心泵,影响规律,机理
0引言
离心泵是应用较为广泛的流体机械[1-2],运行于黄河之上的离心泵会同时遭受沙粒所带来的磨蚀与空化流动所引起的空蚀的协同破坏,易造成严重的经济损失[3]。沙粒的粒径、硬度、密度、形状等固有特性[4],流体作用下的速度、冲击角以及外部环境[5]和不同颗粒的混合都会对水力机械的磨蚀产生不同程度的破坏,其内部流动的本质为包含有相变的汽液固三相流动,与清水介质下的空化流动相比,沙粒的存在显著影响离心泵内空化的发生与发展[6-7]。
现阶段的研究主要集中于不同情况下的磨蚀与空蚀的联合破坏。例如,张涛等[8]获取磨蚀、空蚀及其两者协同作用对Raf6-1翼型破坏的规律。3种不同情况下的翼型所遭受的破坏呈现多样性,且沙粒质量分数与协同破坏程度紧密相关。Gou等[9]通过磁致伸缩仪分析得到颗粒粒径与密度对1045碳钢空蚀与磨蚀联合破坏的影响。在粒径与密度的共同作用下,联合破坏呈现多样性。Hu等[10]通过研究304不锈钢在空化状态下的质量损失、表面形态、粗糙度以及残余应力的变化,发现沙粒质量分数较低时,试件中心区域以磨蚀破坏为主,边缘区域以空蚀破坏为主;沙粒质量分数较高时,试件所有区域均以磨蚀破坏为主。Jin等[11]研究得到固体颗粒对18Cr-8Ni铁空蚀破坏的影响。空蚀或磨蚀单独破坏程度均弱于两者的联合破坏。李彬等[12]研究不同流场压力、冲蚀角、冲蚀速度等对叶轮空蚀与磨蚀联合破坏的影响,获得试件的失重率、破坏形态、破坏痕迹的分布规律。Wang等[13]分析获得颗粒粒径、含量与温度对联合破坏的影响。粒径小于临界值时,联合破坏程度与含量呈反比关系,与粒径和温度呈正比关系。颜大运等[14]探究碳化硅与二氧化硅微型固体颗粒与空化之间的关系,发现颗粒粒径越大,空蚀坑的数目反而越少。Zhao等[15]研究不同材料抵抗磨蚀与空蚀联合破坏的机理,实验结果表明磨蚀与空蚀联合破坏的质量损失量是磨蚀破坏与空蚀破坏单独作用下的两者质量损失量的加权和。廖志康等[16]通过开展HSn70-1锡黄铜的空蚀与磨蚀协同作用的旋转圆盘实验,得到在特定沙粒质量分数与流速下(αs=3%,v=28 m/s),空蚀坑以及磨蚀面积与深度随时间不断变大。赵万勇[17]通过研究运行于黄河之上的泵站,发现泥沙可加剧叶轮的空蚀破坏,同时合理改进叶型并修正进出口安放角可有效抑制空蚀与磨蚀破坏。牛权[18]通过理论推导与分析得到,诱导空蚀与磨蚀对材料联合破坏的核心因素是湍流拟序结构,其表现为微切削,同时与颗粒频率紧密相关。
但离心泵内,不同沙粒质量分数对空化发展的影响规律并未获取,相应的机理也并未揭示。基于此,本文选用粒径为0.020 mm,含量分别为1%、3%、5%与7%的沙粒,开展相应的数值仿真研究,建立不同沙粒质量分数下的空化性能曲线并比较对应的空化余量来确立规律,通过分析沙粒属性、压力、湍动能和空化柔度等的变化来揭示机理。
1数值算法
1.1连续性方程
数值仿真过程,清水介质为主相,水蒸汽与沙粒为次相。清水介质与水蒸汽为连续性介质,沙粒做拟流体处理。因空化所形成的相变与质量传递发生在清水与水蒸汽之间。连续性方程、动量方程、输运方程与相对速度方程[19]为:
式中:ρm为混合相密度;ρv为水蒸汽密度;ρs为沙粒密度;u为混合相速度;x为笛卡尔坐标系下坐标;下标i、j的值分别为1、2、3;p为局部压力;μm为混合相粘度;αv与αs分别为水蒸汽与沙粒的体积分数;me为蒸发源项;mc为冷凝源项;t为时间;vpq为相对速度矢量;vp为次相速度矢量;vq为主相速度矢量。其中,ρm与μm的计算公式为:
式中:ρl为清水介质密度;αl为清水介质体积分数;μl、μv与μs分别为清水介质、水蒸汽与沙粒的黏度。
1.2湍流模型
通过SST k-ω湍流模型[20]求解离心泵内的湍流流动。该模型整合了标准k-ω湍流模型与k-ε湍流模型的优势[21],非常稳健,计算结果精度高。湍动能与湍流耗散率方程为:
式中:k为湍动能,Pk为其对应的生成项;ω为湍流耗散率,Pω为其对应的生成项;FB为混合函数;μ为动力黏度;μt为湍流黏度;α、β、σk、σω均为经验系数;β*与σωout的值分别为0.09与1.176。
1.3空化模型
通过Schnerr-Sauer空化模型[22-23]开展离心泵内空化流动的数值仿真计算,该模型中不存在经验系数,因而通过计算所获结果的精度较高,方程源项为:
式中:ρm--l v为清水介质与水蒸汽间的混合密度;rb为空泡半径;pv为饱和蒸汽压。
2数值仿真准备
2.1物理模型
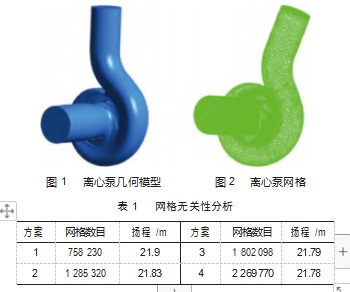
采用型号为M196-100的离心泵开展数值仿真计算,包含有叶轮、蜗壳、进水管路与出水管路4部分,如图1所示。主要性能参数为,设计流量为Qd=100 m3/h,设计扬程为Hd=21 m,转速为n=2 900 r/min。叶轮的主要几何参数为,进口直径Dj=89 mm,出口直径为D2=140 mm,叶轮出口宽度为b2=27 mm,包角为φ=105°,叶片数z=6。
2.2网格划分
鉴于离心泵几何结构复杂,通过ANSYS-ICEM软件选用非结构化网格离散整个计算域,且易于控制网格尺寸与节点数密度,网格如图2所示。采用4种不同数目的网格计算离心泵额定工况下的扬程,开展网格无关性分析。随网格数增加,扬程整体变化较小,最大相对误差小于%,如表1所示。最终选定数目为1 802 098的网格用于开展数值计算。
2.3边界条件与物性参数
通过ANSYS-Fluent开展数值仿真,进口设置为速度,出口设置为压力,由标准壁面函数求解近壁面流动,由SIMPLEC算法求解压力速度耦合方程组,压力项、速度项、湍动能项与湍流耗散率项均全设置为二阶迎风格式,残差为1.0×10-5。清水介质的密度为ρl=998.2 kg/m3,黏度为μl=0.001 kg/(m·s)。沙粒密度为ρs=2 650 kg/m3,沙粒粒径ds=0.020 mm,沙粒质量分数为αs=1%,3%,5%,与7%。
3算法验证
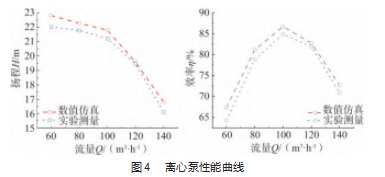
通过图3所示的实验台开展离心泵清水介质下的性能实验,并与数值仿真结果作对比,以此来验证数值算法的可靠性。该实验台包含有模型泵、电机、压力表、流量计、阀门、进水管路与出水管路等。压力表的型号为XU12087105,精度等级为2.5。流量计的型号为DN300,精度等级为1.0。阀门的型号为ZA2.T,精度等级为1.0。
离心泵性能曲线如图4所示。结果表明,扬程与效率的数值仿真结果均略高于实验结果,但最大相对误差分别小于4.2%与4.6%,说明所构建的数值算法可靠,可用于后续开展数值仿真。
4结果与讨论
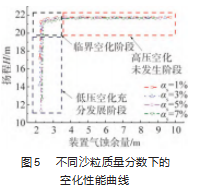
图5所示为沙粒质量分数分别为1%、3%、5%与7%下的空化性能曲线。图中离心泵内空化流动共经历了3个主要阶段,分别为高压空化未发生阶段,临界空化阶段以及低压空化充分发展阶段。为衡量沙粒质量分数对离心泵内空化发展的影响程度,开展不同沙粒质量分数下的临界空化余量与充分发展阶段的空化余量的比较。
经计算临界状态下,空化余量分别为2.24、2.31、2.38与2.45 m;空化充分发展阶段,空化余量分别为2.10、2.23、2.32与2.37 m。结果表明,随着沙粒质量分数的增加,离心泵内空化发展程度不断增强。
图6为不同沙粒质量分数下空泡体积分数为0.1的空泡形态分布情况。发现空泡主要集中在叶轮进口并紧贴叶片吸力面,且同一叶轮不同流道内的空泡形态大小不一。在不同沙粒质量分数下,以流道1中的空泡为研究对象,发现随着沙粒质量分数的增加,空泡沿液体流动方向延伸,所占据的区域变得越来越大,其他叶轮流动中具有相同的变化规律。
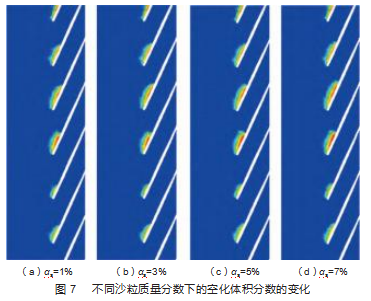
图7为叶轮中间截面空泡体积分数沿径向展开云图。图中展现出空泡沿叶片的分布在不同叶片上不尽相同,但总的来说,随着沙粒质量分数的增加,空泡分布区域变得越来越大,相对应的体积分数也变得越来越高,沙粒质量分数的增加显著促进空化在离心泵内的发展。
5原因分析
5.1沙粒属性
当水中存有沙粒时,会诱导形成空化核子,并逐步发展成为空泡,以此来促进空化的发展。随着沙粒质量分数由1%增加至7%时,沙粒质量分数的增加,会诱导形成更多的空化核子,以此来促进离心泵内空化的发展。另一方面,沙粒具有疏水与不被润湿的性质,使得表面张力显著增强,进而清水介质更易断裂,形成空泡,促进空化流动的发展。随着沙粒质量分数的增加,该过程更易发生,显著促进空化流动在离心泵内的发展。
5.2压力变化
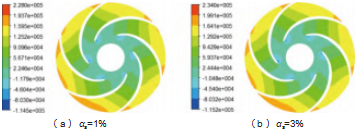
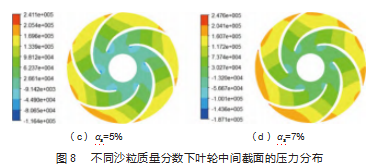
不同沙粒质量分数下,叶轮中间截面的压力分布如图8所示。高压分布在叶轮出口,低压主要集中在叶片背面进口处,这与空泡在叶轮内的分布吻合良好,表明压力对离心泵内空化流动发展的影响较为显著。随着沙粒质量分数由1%增加至7%,最低压力分别为-1.145×105 Pa、-1.152×105 Pa、-1.164×105 Pa与-1.1871×105 Pa,压力显著降低,促进空化流动在离心泵内的发展。
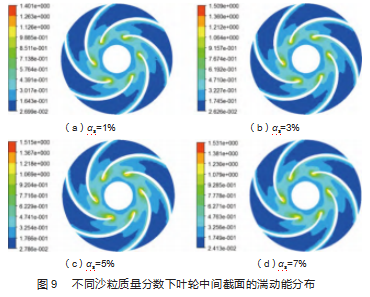
5.3湍动能变化
不同沙粒质量分数下的叶轮中间截面的湍动能分布如图9所示。高强度的湍动能主要集中分布在叶片背面进口处,这与空泡的分布吻合良好。高强度的湍动能使得压力能显著降低,来促进空化的发展。随着沙粒质量分数的增加,最大湍动能不断增大与之相对应的分布区域也不断变大,使得压力能得到显著降低,进而显著促进离心泵内空化流动的发展。
5.4流线变化
不同沙粒质量分数下的叶轮中间截面的流线分布如图10所示。空泡聚集分布区域的流线较为紊乱。随着沙粒质量分数的不断增加,流线紊乱程度有所增强,在其影响下,显著促进空化流动的发展。
5.5空化柔度分析
空化柔度K的变化规律可用于预测空化不稳定性。
式中:Vc为叶轮内的空泡体积;p1为压力监测点。
图11为不同沙粒质量分数下的空化柔度变化情况。发现:不同沙粒质量分数下空化柔度均在正负之间交替变化,当空化柔度值小于0时,压力降低将使空化流场进一步恶化,对比不同沙粒质量分数下的空化柔度变化,发现沙粒质量分数的增加不仅导致空化柔度小于0的范围增大,还使得空化柔度的振幅变化更加剧烈。
6结束语
本文通过数值仿真开展分别为1%、3%、5%与7%的沙粒质量分数对离心泵内空化流动发展影响的研究。通过分析不同沙粒质量分数下的空泡分布、空泡体积分数、临界与充分发展阶段空化余量的变化,确立相应的规律。研究不同沙粒质量分数下的空化核子、压力、湍动能与流线的变化来揭示机理。主要结论如下。
(1)沙粒质量分数由1%增加至7%时,空泡在叶轮内的分布范围变大,空泡体积分数变高,临界空化余量与空化充分发展阶段的空化余量不断变大。沙粒质量分数的增加会显著促进离心泵内空化流动的发展。
(2)随着沙粒质量分数的增加,空化核子数目增多、压力减小、湍动能增强、流线紊乱程度变强。受其综合影响,空化流动在离心泵内的发展显著变强。
(3)随着沙粒质量分数的增加,空化柔度值小于0的范围增加,空化柔度的振幅变化更加剧烈。
参考文献:
[1]王彦军.基于ANSYS CFD的离心泵内部湍流数值模拟分析[J].机电工程技术,2021,50(2):27-29,60.
[2]郝咏冰,宋龙波,乔金宇.基于Excel的离心泵NPSH3预测研究[J].机电工程技术,2019,48(11):92-93,222.
[3]TRUSCOTT G F.A literature survey on abrasive wear in hydrau⁃lic machinery[J].Wear,1972,20(1):29-50.
[4]POSTLETHWAITE J,NESIC S.Erosion in disturbed liquid/parti⁃cle pipe flow:effects of flow geometry and particle surface rough⁃ness[J].Corrosion,1993,49(10):850-857.
[5]FANG Minghao,LIU Fengjiao,MIN Xin,et al.Effect of temper⁃ature on solid particle impact erosion wear mechanism of 5 mol%yttria stabilized zirconia ceramics[J].Ceramics International,2015,41(5):6807-6811.
[6]HAN Xiangdong,KANG Yong,ZHAO Weiguo,et al.Silt particles affect cavitation flow:Analyzing variations in silt mean diameter and concentration[J].Powder Technology,2019,356:671-690.
[7]赵伟国,韩向东,盛建萍,等.沙粒粒径与含量对喷嘴空化的影响[J].上海交通大学学报,2017,51(11):1399-1404.
[8]张涛,陈次昌,郭清.含沙水流中翼型空蚀磨损试验[J].农业机械学报,2010,41(11):31-37.
[9]GOU Wenjuan,ZHANG Hui,LI Huiping,et al.Effects of silica sand on synergistic erosion caused by cavitation,abrasion,and corrosion[J].Wear,2018:120-126.
[10]HU H X,ZHENG Y G.The effect of sand particle concentra⁃tions on the vibratory cavitation erosion[J].Wear,2017:95-105.
[11]Jin,Zheng,Li,et al.The role of sand particles on the rapid de⁃struction of the cavitation zone of hydraulic turbines[J].Wear,1986,112(2):199-205.
[12]李彬.动力学参数对叶轮冲蚀与空蚀交互磨损的影响研究[D].湘潭:湖南科技大学,2014.
[13]WANG Y,WU J H,MA F.Cavitation-silt erosion in sand sus⁃pensions[J].Journal of Mechanical Science and Technology,2018,32(12):5697-5702.
[14]颜大运,汪家道,陈大融.微颗粒影响空蚀破坏的实验研究[J].润滑与密封,2010,35(8):15-18,22.
[15]ZHAO K,GU C Q,SHEN F S,et al.Study on mechanism of combined action of abrasion and cavitation erosion on some en⁃gineering steels[J]Wear,1993,162-164,811-819.
[16]廖志康,刘成龙,高丹丹,等.空蚀与冲蚀联合作用下锡黄铜表面失效形貌演变[J].重庆理工大学学报(自然科学),2015,29(6):41-45,53.
[17]赵万勇.离心泵叶轮汽蚀与泥沙磨损破坏浅析[J].甘肃工业大学学报,2000(1):58-62.
[18]牛权.基于近壁湍流拟序结构的离心泵内沙粒冲蚀角研究[J].水力发电学报,2015,34(5):159-165.
[19]吴小胜,黄晓鹏.计算流体力学基础[M].北京:北京理工大学出版社,2021.
[20]MENTER F R.Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal,2012,32(8):1598-1605.
[21]WILCOX D C.Simulation of transition with a two-equation tur⁃bulence model[J].AIAA Journal,1994,32(2):247-255.
[22]章宇健,常磊鑫,曾乐淘,等.环形激光诱导空化泡的数值仿真分析[J].机电工程技术,2021,50(7):124-129.
[23]SCHNERR G H,SAUER J.Physical and numerical modeling of unsteady cavitation dynamics[C]//Proceedings of the 4th Inter⁃national Conference on Multiphase Flow,Louisiana,USA,2001.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/78127.html