扇形内凹负泊松比结构弹性性能研究

SCI论文（www.lunwensci.com）

　　摘要：文章提出了一种基于泊松比在笛卡尔坐标，对柱坐标系的等效转换下的扇形内凹负泊松比结构。建立了扇形内凹负泊松比胞元结构参数化模型，通过参数相关性分析结构各参数对结构弹性力学性能的相关影响程度，并通过有限元仿真分析，讨论了扇形内凹负泊松比胞元结构的弹性力学性能以及各参数间的对比影响，验证了胞元的负泊松比特性。设计了整体扇形辐射结构，通过有限元仿真分析验证了整体结构的弹性变形性能以及胞元设计的有效性，最后讨论分析了整体结构最终变形结果与胞元泊松比设计值差异产生的原因。

　　关键词：柱坐标系；负泊松比；弹性力学性能；有限元分析；参数相关性分析

　　1研究背景和意义

　　负泊松比超材料作为一种具有独特力学性质的新型材料，近年来受到了广泛关注。负泊松比是指材料在某一方向上的压缩（或拉伸）会导致其作用垂直方向上发生收缩（或膨胀）。这种独特的力学特性将为各种潜在的工业、医学和生物工程领域提供力学支持和多重应用［1］。自从Gibson［2］等人首次引入自主设计的具有负泊松比特性的蜂窝形状以来，研究者通过几何结构的创新，相继提出了双箭头胞元结构［3］、星型胞元结构［4］，不断深化对胞元理论的研究。近几年的研究中，旋转多边结构以及手性结构等新型的胞元结构也层出不穷［5］。

　　为了进一步拓宽负泊松比结构多种形状应用，文章提出一种基于柱坐标系工况下的扇形负泊松比结构，通过扇形胞元面内旋转分布的设计形式，揭示其独特力学特性和应用前景，为负泊松比材料的特殊形状场景研究提供有益的参考和启示。

　　2扇形负泊松比结构等效设计

　　2.1微观结构弹性性能等效转换

　　材料的弹性性能通常是通过应力和应变引申的各种关系来表征的。对于笛卡尔坐标来说，材料在y方向上的泊松比υ定义为横向应变εx与纵向应变εy之比：

　　同时εx和εy也可以由材料在x和y方向的应σx和σy决定：

　　将这些公式从笛卡尔坐标系等效转换到柱坐标系，则根据材料在柱坐标系周向的分布角度θ0以及旋转后的角度增量Δθ、径向长度r0以及变形后的径向增量Δr可知：

　　2.2扇形内凹负泊松比胞元结构设计

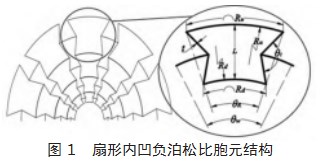
　　将笛卡尔坐标系x-y轴转换成柱坐标系θ-r轴，基于经典内凹直杆结构构造出如图1所示扇形内凹结构。新结构具有以下特征及相应参数：

　　（1）扇形特征：结构扇形分布，上、下弧长R、R分别由上下弧长半径Ru、Rd及上下弧周向张开角度θR决定。

　　（2）同心圆特征：R和R与胞元两侧共享连接弧都保持同心圆特征。

　　（3）径向特征：径向特征长度L=Ru-Rd表征胞元结构的径向分布。

　　（4）周向特征：两端圆心角θw表征胞元结构的周向分布角度。

　　（5）内凹特征：驱动胞元结构内凹程度的特征角度θt。

　　（6）胞元厚度t也是该结构的重要参数。

　　2.3设计参数的确定

　　为方便建立参数化模型，舍去重复约束尺寸R、R和Rd，保留关键设计参数Ru、θR、L、θw、t以及θt。通过Ansys Workbench参数相关性分析模块得到这6个参数对结构响应的相关性，如图2所示。

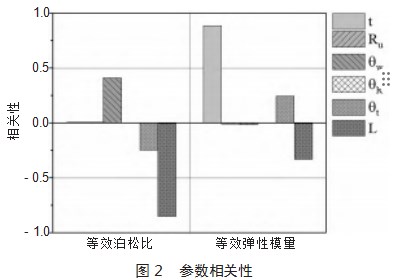
　　可以看到，L对等效泊松比的影响程度最大且呈负相关，即结构负泊松比效应越明显。θw与等效泊松比呈正相关，而对等效弹性模量几乎没有影响。参数t与等效弹性模量呈正相关，而对等效泊松比几乎没有影响。Ru和θR都对等效泊松比和等效弹性模量几乎没有影响。

　　3胞元结构弹性性能有限元分析

　　3.1有限元模型的建立及求解

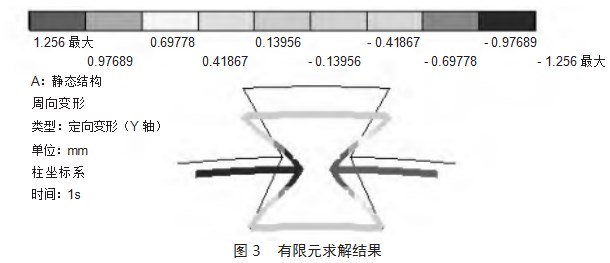
　　建立扇形胞元参数化模型，给定Ru=100mm，θR=6。，L=10mm，θw=12。，θt=126。，t=1mm。基底材料E0=200GPa，υ0=0.3。定义圆柱坐标系，单元类型beam188，下弧边施加固定约束，上弧边径向压缩Δr=2mm。求解结果如图3所示。

　　施加压缩载荷后，胞元两侧向内收缩，周向角度变化量Δθ=2.512rad，求得该胞元结构的泊松比为-0.631，符合负泊松比的变形特征。

　　3.2径向应变εr的影响

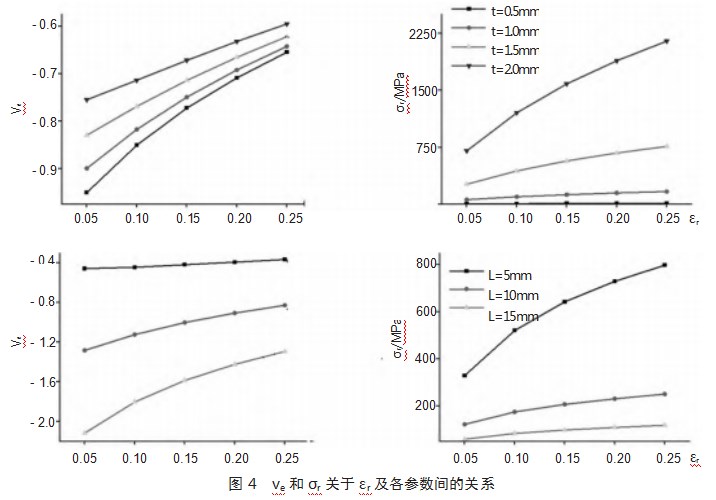
　　在柱坐标径向方向上，施加扇形胞元在［0.05，0.25］范围内不同径向应变εr。有限元分析结果如图4所示。

　　可以看出，胞元结构的泊松比并不是线性的。随着εr大，胞元结构负泊松比效应逐渐减弱，径向非线性应力σr随之增大。

　　3.3胞元尺寸缩放的影响

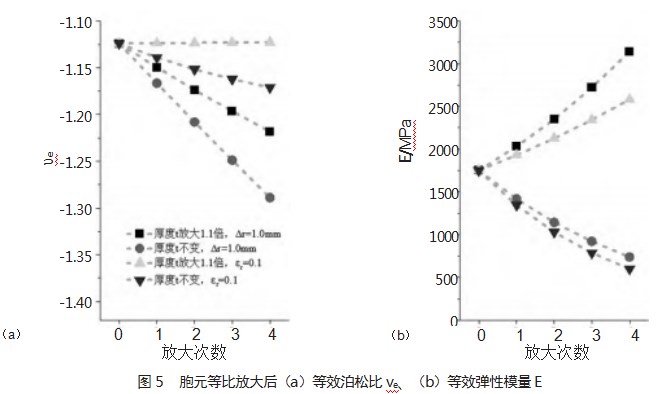
　　固定θt=150°、θR=6°、θw=10°,并以Ru=110mm、L=10mm的胞元作为整体结构基准层。随后每递增一层，Ru和L的值均按照1.1倍的等比递增。以下是基于这种胞元尺寸等比缩放情形下的有限元分析结果。

　　从图5（a）可知，如果t也放大1.1倍，即厚度横截面积放大1.12倍，各胞元的等效泊松比几乎是相等的。如图5（b）所示，随着放大次数的增加，等效弹性模量逐渐增加，表明胞元抵抗变形的能力增强。

　　4扇形内凹负泊松比辐射结构的有限元分析

　　基准层胞元参数θw=10°、θR=6°、θt=131.2°、t=1mm、L=8mm，按照1.08倍放大各层胞元。建立整体辐射结构有限元模型，单元类型solid186，计算结果如表1所示。

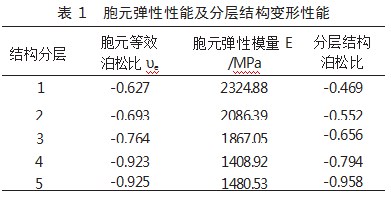
　　结果显示，施加径向压缩时，分层结构周向也出现收缩特征，表现出负泊松比特性，验证了柱坐标系下扇形胞元设计以及对整体结构设计的可行性。尽管整体结构展现出了与预期相符的负泊松比特性，但分层结构泊松比的具体表现数值与胞元设计数值存在一定的偏差。这种偏差的产生主要有以下原因：

　　4.1各层胞元等效弹性模量的差异

　　在给定的压载下，各层胞元受到相同径向压力，但由于各层胞元的等效弹性模量存在差异，导致其径向应变各不相同，进一步影响胞元的等效泊松比。

　　4.2非理想变形产生的误差

　　在结构变形过程中，由于各层胞元受到其他层胞元的牵拉、挤压以及自身上下弧边的不对称压缩，导致了周向上的偏移误差。

　　5结论与展望

　　文章通过等效泊松比的坐标转换，设计出基于柱坐标系下的扇形内凹负泊松比结构。通过参数相关性分析和有限元数值仿真分析，深入探讨了该结构的弹性力学性能以及各参数对等效泊松比的影响。此外，文章通过设计整体扇形辐射结构，验证了扇形胞元弹性性能。文章研究不仅揭示了扇形内凹负泊松比结构的独特弹性力学特性，同时也为其应用于环管状变形场景的应用提供了有益的参考和启示。

　　参考文献

　　［1］于相龙，周济.力学超材料的构筑与超常性能［M］.合肥：中国科学技术大学出版社，2021.

　　［2］Lorna J，Gibson.多孔固体结构与性能［M］.刘培生，译.北京：清华大学出版社，2003.

　　［3］Larsen U D，Sigmund O，Bouwstra S.Design and fabrication of compliant micromechanisms and structures with negative Pois-son's ratio［J］.IEEE，1996.

　　［4］GrimaN J，Gatt R，Alderson A，et al.On the potential of connect-ed stars as auxetic systems［J］.Molecular Simulation，2005，31（13）：925-935.

　　［5］任鑫，张相玉，谢亿民.负泊松比材料和结构的研究进展［J］.力学学报，2019，51（3）：656-687.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/77578.html