基于最小二乘法优化的柔性机械臂自抗扰控制方法论文

SCI论文（www.lunwensci.com）

　　摘要：常规的柔性机械臂自抗扰控制方法多数采用微分平台原理，对机械臂的自抗扰控制器进行设计，控制精度较低，无法提高柔性机械臂的自抗扰性能，导致机械臂受到扰动作用时，各个关节角度容易发生大幅度变化。基于此，引入最小二乘法，对常规柔性机械臂自抗扰控制方法进行了优化设计。采用拉格朗日功能平衡法原理，优化柔性机械臂动力学模型，获取机械臂系统动能与势能变化，在此基础上，利用最小二乘法，优化设计机械臂自抗扰控制器，补偿机械臂系统自抗扰控制量。实验分析可知，通过提出方法进行柔性机械臂自抗扰控制，在综合扰动作用下，机械臂各个关节角度的变化幅度均较小，在±1°以内，关节角均未发生明显运动改变，控制精度较高，能够显著提升机械臂的自抗扰性能，具有可靠的应用性。

　　关键词：最小二乘法；优化；柔性；机械臂；自抗扰；控制

　　Abstract:Most of the conventional active disturbance rejection control(ADRC)methods for flexible manipulators use the differential platform principle to design the ADRC of the manipulator.The control accuracy is low,and the ADRC performance of the flexible manipulator cannot be improved.As a result,when the manipulator is disturbed,the joint angles are prone to change significantly.Aiming at this issue,the least square method is introduced to optimize the ADRC of conventional flexible manipulators.Using the principle of Lagrangian functional balance method,the dynamic model of the flexible manipulator is optimized to obtain the changes of the kinetic energy and potential energy of the manipulator system.On this basis,the least square method is used to optimize the design of the manipulator ADRC to compensate the ADRC of the manipulator system.Experiment analysis results show that using the proposed method for the ADRC of the flexible manipulator,under the comprehensive disturbance,the change amplitude of each joint angle of the manipulator is small,within±1°,there is no significant movement change in the joint angle.Therefore,the control accuracy is high,the automatic disturbance rejection performance of the manipulator is significantly improved,and the application is reliable.

　　Key words:least square method;optimization;flexibility;mechanical arm;self disturbance rejection;control

　　0引言

　　柔性机械臂作为机器人的重要组成部分，对机器人的操作与控制具有较大影响。基于广义角度分析，柔性机械臂属于一种精密度较高的工业化产品，在一定程度上能够满足工业生产与发展的需求[1]。柔性机械臂的主要组成材料为柔性材料，利用其制作成质量较轻的连杆结构，一方面能够实时驱动机器人的关节控制，另一方面能够提高机械臂的定位精度[2]。由柔性机械臂组成的工业机器人与其他类型工业机器人相比，在结构与性能方面均存在一定的差异。传统工业机器人多数由刚性材料组成，其整体基座结构相对笨重，操作控制空间局限性较强，且机器人控制与操作的灵活性较差[3]。柔性机械臂机器人整体质量较轻，操作过程中产生的功耗较低，操作控制空间打破了局限性，且控制与操作的灵活性与灵敏性较好[4]。现阶段，针对柔性机械臂的研究逐渐成熟，能够满足现代化工业生产自动化的需求。然而，在柔性机械臂自抗扰控制方面的研究仍然不够完善。主要体现在传统机械臂自抗扰控制方法不能较好地抑制其弹性振动，对于柔性机械臂运行过程中的动态特性描述不清晰，无法提高机械臂的抗干扰性，降低了柔性机械臂操作定位的精度与效率[5]。

　　基于此，本文在传统柔性机械臂自抗扰控制方法的基础上，引入最小二乘法，对传统控制方法作出了优化设计，为提高机器人质量、推动工作生产自动化的发展作出贡献。

　　1柔性机械臂自抗扰控制方法优化设计

　　1.1动力学模型

　　本文优化设计基于最小二乘法的柔性机械臂自抗扰控制方法。首先，采用拉格朗日功能平衡法原理，对当前传统的柔性机械臂动力学模型进行优化改进设计，为后续的机械臂自抗扰控制提供基础保障。

　　传统的柔性机械臂动力学模型多数采用牛顿-欧拉动态平衡法原理，根据机械臂控制系统内作用力的动态变化，建立机械臂动力学模型。通过此种方法原理建立的动力学模型与柔性机械臂实际操作控制情况存在一定的偏差，且模型建立流程复杂，局限性较强，无法满足工业生产自动化的需求[6-7]。本文采用的拉格朗日功能平衡法，其只需要对柔性机械臂的变量进行计算，根据计算结果进行动力学模型建立，不需要求取柔性机械臂控制系统内作用力，整体计算与建模流程更加简单，适用范围较广泛[8-10]。

　　首先，在广义坐标范围内，定义柔性机械臂控制系统的拉格朗日功能函数，其表达式为：

　　L=K-P(1)

　　式中：L为柔性机械臂的拉格朗日系数；K为柔性机械臂系统总动能；P为柔性机械臂系统势能。

　　基于柔性机械臂的拉格朗日系数，建立动能与势能关系方程：

　　式中：δi为柔性机械臂动能与势能广义坐标内的广义力；qr1为柔性机械臂的广义速度；qr为柔性机械臂动能与势能的广义坐标；d、t、φ分别表示柔性机械臂操作控制过程中的任意系数。

　　通过柔性机械臂拉格朗日方程表达式可知，本文优化的机械臂动力学模型中，主要包括对柔性机械臂系统的动能与势能两个部分的计算，接下来，进行具体计算与说明。首先，基于柔性机械臂系统的动能来说，其表达式为：

　　K=K0+K1+K2(3)

　　式中：K0为全方位移动柔性机械臂的初始动能；K1、K2分别为柔性机械臂系统中连杆1、连杆2的动能。

　　通过计算，获取到柔性机械臂系统的动能，接下来，对柔性机械臂系统的势能进行计算。本文采用微质点动能积分的方式，在广义坐标内，对柔性机械臂的连杆结构作出了分解，其结构如图1所示。

　　图中所示为本文分解的柔性机械臂连杆结构，其中，N为柔性机械臂连杆上的任意一点，距离其旋转轴长度为l，对连杆的转动惯量进行分析，在此基础上，计算柔性机械臂系统动能，公式为：

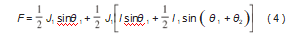
　　式中：J1为柔性机械臂连杆转动惯量；θ1、θ2分别为柔性机械臂连杆对应的夹角。

　　通过以上计算获取到柔性机械臂系统动能与势能，将其结合在一起，生成全新的基于拉格朗日功能平衡法的柔性机械臂动力学模型，描述机械臂的动态变化，完成传统机械臂动力学模型优化[11-12]。

　　1.2基于最小二乘法优化机械臂自抗扰控制器

　　在柔性机械臂动力学模型优化结束后，获取到柔性机械臂系统的动能与势能，在此基础上，采用最小二乘法，对机械臂自抗扰控制器进行全方位、多维度的优化设计，进而提高机械臂的抗干扰性能。

　　本文首先对柔性机械臂的自抗扰控制器运行原理进行了分析，其控制器原理如图2所示。从图可知，柔性机械臂自抗扰控制器主要包括3个部分，分别为机械臂跟踪-微分器TD、机械臂非线性状态误差反馈-控制律NLESF与机械臂在干扰作用下扩张状态观测器ESO[13]。其中，z 1、z2、z3分别为柔性机械臂系统状态变量对应的估计值；e 1为柔性机械臂系统自抗扰控制误差信号；e2为柔性机械臂系统自抗扰控制误差的微分信号；v 1为TD跟踪微分器运行过程中输出的跟踪信号；v2为TD跟踪微分器运行过程中输出的微分信号；u0为柔性机械臂系统非线性状态误差反馈控制律；u为柔性机械臂系统非线性状态误差反馈控制律输出结果。

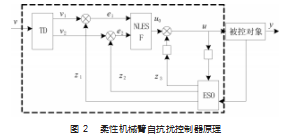
　　基于图2的柔性机械臂自抗扰控制器原理，利用最小二乘法，对柔性机械臂自抗扰线性空间参数进行识别。最小二乘法属于数学技术中较为优化的一种，能够寻找到柔性机械臂自抗扰线性空间参数中的最佳函数匹配，进而减小识别结果与实际结果之间的误差，实现提高机械臂自抗扰控制精度的目标。柔性机械臂自抗扰线性空间参数识别的最小二乘法表达式为：

　　y=α1 x 1+α2 x2+…+αn xn(5)

　　式中：α=(α1,α2,…,αn)为柔性机械臂自抗扰线性空间测量值；y为柔性机械臂系统观测值；x为柔性机械臂系统输入值。

　　利用最小二乘法表达式，对柔性机械臂自抗扰线性空间参数进行识别，优化其自抗扰控制识别结果，不断更新数据，提高机械臂自抗扰控制的效率。

　　在此基础上，结合柔性机械臂自抗扰控制识别结果，优化设计机械臂自抗扰控制器，结构如图3所示。图中，利用最小二乘法优化设计后的自抗扰控制器主要采用内外环的控制结构，其中，包括自抗扰控制位置子系统、自抗扰控制姿态子系统与机械臂系统。基于自抗扰控制位置子系统来说，主要由位置控制器与速度控制器组成；自抗扰控制姿态子系统由姿态控制器与角速度控制器组成[14-15]。优化后的柔性机械臂自抗扰控制器属于一个耦合的结构，有效地避免了机械臂摆动的扰动影响，将机械臂系统外部扰动与内部扰动相结合，形成了各个通道的总扰动。机械臂系统实时对各个通道的总扰动进行估计，获取对应的估计值后，将其补偿到机械臂系统控制量的输出中，进而全方位实现柔性机械臂自抗扰控制的目标，完成优化设计。

　　2实验分析

　　综合第1章内容，本文采用最小二乘法优化设计柔性机械臂自抗扰控制方法的整体流程。在此基础上，为了进一步验证本文提出方法的可行性与应用优势，进行了如下实验。

　　2.1实验准备

　　本次实验选取“漫游者”系列机器人为研究对象，该系列机器人的机械臂属于水下柔性机械臂。该机器人的机械臂的防护等级为IP30，本体质量为205 kg，包含4个旋转轴，有效荷载为30 kg，重复定位精度为0.5 mm，最大臂展为1 820 mm，惯性力矩为1.45 kg/m2，振动小于4.9 m/s2。

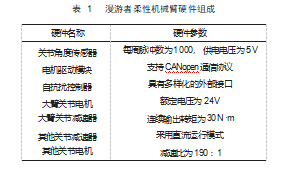
　　为了更加清楚地了解机器人柔性机械臂的实际情况与信息，对该机械臂的硬件组成进行了分析，如表1所示。表中为选用漫游者系列机器人柔性机械臂的硬件型号及对应的参数。在掌握柔性机械臂相关信息后，搭建10 m深的水池，将漫游者系列机器人柔性机械臂放入水池中，利用上述本文优化设计的自抗扰控制方法，对机器人柔性机械臂进行全面控制。

　　2.2结果分析

　　本次实验通过对漫游者系列机器人柔性机械臂不同关节赋予不同频率的正弦信号，获取柔性机械臂各个关节的自抗扰控制效果，并对控制效果作出分析。设定水下测试实验时间为20 s，其中，柔性机械臂肩关节自抗扰运动周期为20 s，相应的幅度为20°；柔性机械臂大臂关节与肘关节自抗扰运动周期为10 s，相应的幅度为30°。为了更加直观地验证本文提出自抗扰控制方法的有效性，采用对比分析的实验方法。将文献[1]提出的柔性机械臂自抗扰振动抑制方法、文献[2]提出的机械臂西康绕鲁棒控制方法，与文本提出的基于最小二乘法优化的柔性机械臂自抗扰控制方法进行对比。在静水条件下，采用MATLAB分析软件，测定3种自抗扰控制方法应用后，在扰动测试周期内，柔性机械臂3个关节角度的动态变化，如图4(a)~(c)所示，根据关节角度的动态变化，判断柔性机械臂自抗扰控制效果。

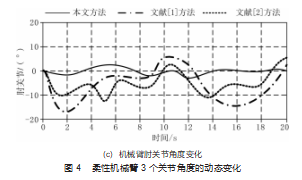
　　从图4(a)~(c)的变化趋势可知，在3种柔性机械臂自抗扰控制方法中，本文提出的基于最小二乘法优化的柔性机械臂自抗扰控制方法应用后，在测试周期内，受到综合扰动作用，机械臂3个关节角度的变化幅度均较小，在±1°以内，关节角均未发生明显运动改变，控制精度较高，较另外两种自抗扰控制方法相比，柔性机械臂的肩关节、大臂关节与肘关节角均能保持平稳的运行。由此可见，本文设计的控制方法的控制精度较高，应用效果优势显著，能够显著提升柔性机械臂的自抗扰性能。

　　3结束语

　　综上所述，为了改善传统柔性机械臂自抗扰控制方法在实际应用过程中存在控制精度较低，无法提高柔性机械臂的自抗扰性能，机械臂在受到扰动作用时，各个关节角度容易发生大幅度变化等问题，在传统控制方法的基础上，提出了一种全新的机械臂自抗扰控制方法，利用最小二乘法，优化设计机械臂自抗扰控制器，补偿机械臂系统自抗扰控制量。通过本文研究，有效降低了柔性机械臂自抗扰控制过程中存在的不确定性，提高了机械臂自抗扰控制在综合扰动作用下的效率与精度，优化了柔性机械臂的抗干扰性，使其稳态性能能够发挥至最优效果，为工业领域提供可靠的技术参考和帮助。

　　参考文献：

　　[1]潘昌忠,罗晶,李智靖,等.平面欠驱动柔性机械臂的PSO轨迹优化与自抗扰振动抑制[J].振动与冲击,2022,41(14):181-189.

　　[2]曾庆山,周亚帅,陶长春,等.电驱动机械臂的自抗扰鲁棒哈密顿跟踪控制[J].郑州大学学报(工学版),2022,43(4):1-7.

　　[3]仲训杲,仲训昱,彭侠夫,等.未知雅可比建模的机器人视觉伺服自抗扰控制方法[J].厦门大学学报(自然科学版),2022,61(2):231-238.

　　[4]王刚,李小华.柔性关节机械臂的自抗扰预设定有限时间跟踪控制[J].辽宁科技大学学报,2021,44(5):363-370.

　　[5]秦洪浪.基于递推最小二乘法的仿人机械手控制技术研究[J].自动化仪表,2021,42(8):30-36.

　　[6]刘淑香.基于最小二乘法的桥式起重机机械臂关节控制系统设计[J].计算机测量与控制,2021,29(5):97-101.

　　[7]邱炯智,张宪文,李汶杰,等.一种基于最小二乘法的移动机器人拾取臂控制系统研究[J].机电工程技术,2020,49(5):79-81.

　　[8]张月龄,向国菲,税懿,等.基于解耦双通道线性自抗扰控制的连续型机械臂轨迹跟踪策略[J].空间控制技术与应用,2020,46(5):27-35.

　　[9]崔士鹏,孙永军,刘伊威,等.柔性关节机械臂最优控制方法研究[J].电机与控制学报,2021,25(5):119-130.

　　[10]马天兵,宫晗,杜菲,等.基于线结构光和优化PID的压电柔性机械臂振动控制[J].光学精密工程,2021,29(11):2661-2671.

　　[11]孙绍林.区分快慢变子系统的柔性机械臂控制方法[J].机械设计与制造,2021(1):175-178.

　　[12]华攸水,张浩,罗健,等.9自由度爬行焊接机器人控制系统[J].自动化与信息工程,2022,43(5):8-12.

　　[13]刘福才,刘林,郭根旺.柔性关节空间漂浮机械臂奇异摄动自抗扰控制仿真研究[J].高技术通讯,2020,30(9):928-937.

　　[14]姜海勇,邢雅周,李娜,等.基于微分平坦与自抗扰控制的伸缩臂抖动抑制研究[J].农业机械学报,2020,51(3):394-401.

　　[15]郑怀航,王军政,刘冬琛,等.融合前馈与姿态预测的并联稳定平台自抗扰控制策略[J].机械工程学报,2021,57(9):19-27.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/66011.html