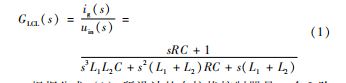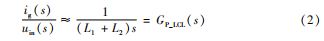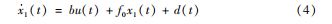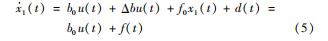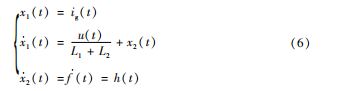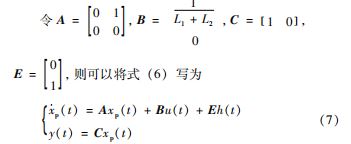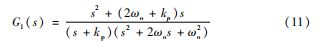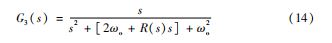基于改进自抗扰的LCL并网逆变器控制方法论文

SCI论文（www.lunwensci.com）


　　摘要：为改善并网逆变器动态性能和入网电流波形质量，提出一种改进的降阶自抗扰控制方法。将谐振控制器加入到自抗扰扩张观 测器的前馈通道中形成比例谐振控制(PR )，可以有效提高自抗扰控制器对并网电流谐波的抑制能力。对LCL 并网逆变器数学模型 进行降阶处理，并分析线性自抗扰(LADRC ) 控制器的设计原理和参数整定;给出改进后自抗扰控制( PR-LADRC ) 的扰动传递 函数，并分析控制器的性能;通过实验验证控制器的有效性。结果表明：所设计的控制器在不改变自抗扰动态性能的情况下在谐波 抑制方面有较好的优势。
　　Abstract：In order to improve the dynamic performance and quality of the inverter，an improved reduced order active disturbance rejection control strategy is adopted.The resonant controller is added to the feedforward channel of the expanded observer of the active disturbance rejection controller to form a proportional resonant controller ( PR )，by which the ability of the active disturbance rejection controller to suppress grid connected current harmonics can be effectively improved.The mathematical model of the LCL grid connected inverter is reduced，and the design principle and parameter tuning of linear active disturbance rejection ( LADRC ) controller are analyzed;the transfer function of improved active disturbance rejection control ( PR-LADRC ) is given，and the performance of the controller is analyzed;the effectiveness of the controller is verified by experiments.The results results show that the designed controller has better advantages in harmonic suppression without changing the dynamic performance of ADRC.

　　Key words：inverter;active disturbance rejection control;extended observer;roportional resonance control

　　0 引言

　　并网逆变器作为可再生能源发电单元与电网连接的 重要装置，逆变器的性能直接决定着入网电流质量[1-4] 。

　　然而并网逆变器系统存在的死区效应、开关管导通压降 以及电网电压波动等非线性因素，常常使逆变器难以保 持良好的性能。因此，采用优越的控制算法改善逆变器性能成为当前研究的热点。

　　目前，对逆变器的控制策略主要有比例-积分(PI) 控制、比例-谐振( PR ) 控制、重复控制。文献[5 ]提出了一种PI 控制和电容电流反馈的控制方法，在前向 通路中加入了滞后补偿环节，从而改变环路的穿越情况， 但该类方法会减少系统的相位裕度，不利于系统的动态响应能力。文献[6-7 ] 讨论了用逆变器的准比例谐振( PR ) 控制策略，取得了较好的控制效果，但是该PR 控制器对高次谐波的抑制能力不足。文献[8-9 ] 提出了重复控制与其他控制相结合的复合控制方法，但是重复控制无法选择个别谐波进行最优补偿，同时还存在重复 控制原理复杂、实现难度大等问题。

　　自抗扰控制器(ADRC ) 作为一种新兴的控制技术 在工程控制中被国内外大量学者运用于不同领域，目前 在并网逆变器中的应用还比较少。文献[10 ] 将非线性 ADRC 算法运用到电压型PWM 逆变器系统中，取得了较 好的控制效果，但是非线性自抗扰设计复杂，参数调节 难度大。文献[11 ] 提出了一种利用LCCL 型滤波器将3 阶系统降为1阶的微分前馈自抗扰控制，减小了控制器 设计难度，并提高了控制器的跟踪精度，但是微分前馈的加入会放大高频谐波，导致输出波形THD 增大。文献[ 12-13 ] 采用了一种改进扩张观测器的自抗扰控制器降低了直流侧母线电压的纹波，提高了系统的抗扰性能， 但是系统参数调节复杂，不利于在工程中运用。

　　本文以LCL 型并网逆变器为控制对象，将3阶逆变 器模型利用Padé 近似等效为1阶模型，根据等效模型设计一种结构简单、参数易于调节且有利于在工程中使用 的降阶自抗扰控制;在扩张观测器中加入谐振控制，有 效提高了谐波抑制能力;通过实验对所设计的控制器进 行了验证。

　　1 LCL 型并网逆变器模型

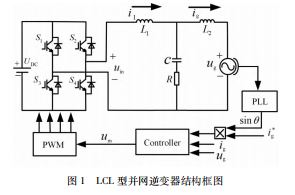
　　图1所示为LCL 型并网逆变器的拓扑结构图。其中， UDC 为直流母线电压;S1 ~ S4 为开关管;uin 为LCL 滤波器 的输入电压;LCL 滤波器由逆变侧电感L1 、电网侧电感 L2 、滤波电容C和阻尼电阻R组成。i1 、ig 分别为逆变器侧 电流和电网侧的电流;ug 为电网电压;ig* 为参考电流的幅 值。

　　入网电流ig 到逆变器输出电压uin 的传递函数为，

        根据公式(1 ) 所设计的自抗扰控制器是一个3 阶 控制器，但是高阶自抗扰结构复杂，需要对多个状态变 量进行微分，待整定参数较多，不利于在工程中使用。 由于自抗扰控制器可以把建模误差当作内扰的一部分，在进行自抗扰控制器设计时并不需要精确的控制对象模型。因此，低阶自抗扰控制器在实践中通常是首选[13]，在此用1阶系统模型近似代替3 阶系统模型进行控制器 设计。采用Padé 近似的方法对式(1 ) 进行降阶处理，降阶后入网电流ig 到输出电压uin 的传递函数为：

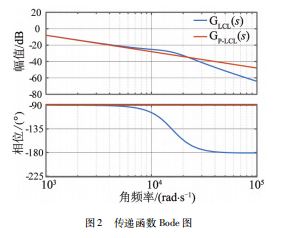
     GLCL (s ) 和GP_LCL (s ) 传递函数的Bode 图如图2所示。

　　由图可知，2 个传递函数在低频段完全一致，反馈控制 器主要校正的也是系统的低频特性。并且从自抗扰控制 器将建模误差视为“广义扰动”的角度而言，即使降阶 模型在高频处存在的误差对系统产生不利影响也会被自 抗扰的状态观测器估计并在补偿环节实施补偿以消除。 因此，将3阶LCL 并网逆变器模型进行降阶处理是可行 的，只要扩张观测器能够准确估计总扰动并进行补偿，所设计的1阶自抗扰控制可以达到与3 阶自抗扰控制相 当的效果，而且有利于在实际工程中运用。

　　2阶自抗扰控制器设计

　　为简化LCL 并网逆变器控制系统结构，提高控制器 在工程中的应用价值，对系统进行降阶线性自抗扰控制 器设计。

　　2.1 LADRC 的并网电流控制器设计

　　降阶后的LCL 型并网逆变器传递函数为式(2 )，可 以推导出电网电流ig 的微分为：

　　假设系统的数学模型未完全已知，并考虑外部干扰d ( t )，在自抗扰控制框架下，LCL 型并网逆变器的系统模型可以重新表述为：

　　式中：x 1 ( t ) = ig ( t ) 为控制电流;u ( t ) 为控制输入变量。 设b= b0 + Δb，其中b0 = 1/(L1 +L2 ) 表示模型中的已知 部分，Δbu( t ) +f0 x 1 ( t ) 表示并网逆变器中建模的未知部分，比如滤波参数中摄动引起的参数偏差。式(4 ) 又可以写为：

　　式中：f( t ) = Δbu( t ) +f0 x 1 ( t ) + d ( t ) 表示并网系统中的总扰动量，包括系统内部扰动和外部扰动。

　　设x2 (t ) = f(t )，矩阵xp (t ) = [ x1 (t ) x2 (t ) ] T，y (t ) 为系统的输出。其中x2 ( t ) 为扩展的状态变量。用h( t ) 表示f(t ) 的1 阶导数，因此可以根据式(5 ) 将降阶后的并网逆变器的状态空间方程写为：

　　式(7 ) 为重构后包含系统总扰动的降阶LCL 型并 网逆变器状态空间表达式。

　　2.2 线性扩张观测器( LESO ) 设计

　　设z( t ) = [ z1 ( t ) z2 ( t ) ] T，其中z1( t ) 和z2( t ) 分别 表示状态变量x1 ( t ) 和x2 ( t ) 的估计值，即电网电流 ig ( t ) 和总扰动f(t ) 的估计值。β = [β1 β2 ] T 为LESO 的带宽参数，通过选择合适的参数，可以使观测器状态变 量快速跟踪系统的状态变量。结合式(7 ) 可以得出LESO 的表达式为·

                                                       z(t ) = (A -βC)z (t ) + Bu (t ) +βx1 (t )             (8 )

矩阵(A -βC) 的特征值决定了观测器误差衰减速率。

　　2.3 线性控制律设计

　　根据文献[14 ] 设计降阶后的LCL 并网逆变器的线性控制率(LSEF ) 表达式为
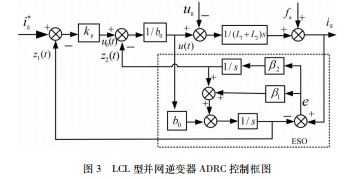
　　式中：u0 ( t ) 为LSEF 的输出信号;kp 为LSEF 中的增益，那么1阶自抗扰控制器的控制律为综上所述，LCL 并网逆变器的1阶ADRC 控制系统 框图如图3所示图中fa 为测量干扰是总扰动的一部分，为简化ADRC 控制器的参数整定过程，通常采用带宽法[13] 控制器参数kp、β 1 、β2 进行归一化处理。设ω0 、ω c 分别为观测器带宽和控制器带宽，则β1 = 2 ω0.β2 = ω0(2)，kp = ω c。

　　为保证LESO 对总扰动的观测精度并能够对总扰动进行实时补偿，观测器带宽ω0 一般取(2 ~ 10 ) ω c [ 15 ] 。

　　2.4 PR-ADRC 控制的改进自抗扰控制器设计

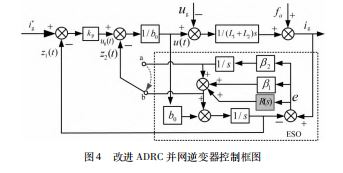
　　为进一步提高自抗扰控制对并网电流谐波的抑制能力，在自抗扰控制的扩张观测器中加入PR 控制器对电 流谐波进行抑制，并通过改变扩张观测器的扰动前馈通 道，使得控制器参数调节更为容易。控制框图如图4 所示。

　　与图3相比，图4进行了两点改进：

　　( 1 ) 将图3中的ADRC 控制器扰动前馈通道由a切换到b。在图3 中利用梅森增益公式推导出线性自抗扰 在系统中的扰动传递函数为

         式(11 ) 中扰动传递函数的控制器带宽kp 和观测器 带宽ωo 相互耦合，给参数调节带来了一定的困难。为降 低参数调节的难度，将控制器的扰动前馈通道由a切换 到b，利用梅森公式得出改进后的扰动传递函数为

         可以看出式(12 ) 中扰动传递函数只与观测器带宽ω o 有关，这为参数调节降低了难度。

　　(2 ) 在自抗扰控制器的ESO 环节加入了谐振控制器 R (s )，使R(s ) 与β1 构成PR 控制器，提高系统对谐波的 抑制效果。R (s ) 的传递函数为

　　式中：kr 为谐振控制器的增益;ωｃ 为谐振控制器的带宽ω１ 为谐振频率。
改进后系统的扰动传递函数为

　　在式(14 ) 中，当工作频率在ω1 附近时R(s ) 将有 无穷大增益，此时[2 ωo + R (s )] 将变大，而传递函数G3 (s ) 的幅值|G3 (s ) | 将变小，所以逆变器在谐振频率附近工作时对逆变器谐波的抑制能力将会提高。

　　2.5 PR 控制的改进自抗扰性能分析

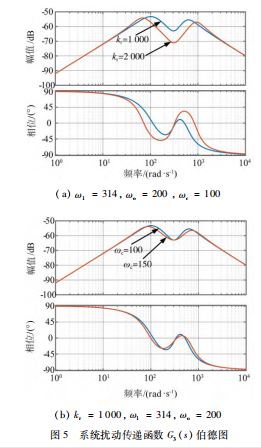
　　为验证所提方案在并网逆变器控制中的有效性，通 过伯德图分析改进PR-ADRC 控制抗扰能力。

　　设置ω1 = 314.即电网频率为50 Hz 时，ω o = 200 、ω c = 100 为固定值，令kr 为1000、2 000.系统扰动传递
函数伯德图如图5 ( a ) 所示。由图可知，在低频段和高频段改变kr 时，系统对扰动的抑制效果没有明显增加， 但是在基波频率ω1 = 314 时，随着kr 的增加，系统对扰 动的抑制效果有明显提高。设置ω 1 = 314 、ω o = 200 、kr = 1 000.令ωc 为100、150.系统扰动传递函数伯德图如图5( b ) 所示。由图可知，在低频段和高频段增大ωc时，系统对扰动的抑制能力没有变化，但是在电网基波 频率附近处，随着ωc 增大，系统对扰动抑制的带宽会明 显变大。因此，在自抗扰控制器的扩张状态观测器环节中 加入PR 控制器，通过选择适当的参数能够使LCL 并网逆 变器对电网电压等因素引起的扰动具有更强的抗扰性。

　　3 实验验证

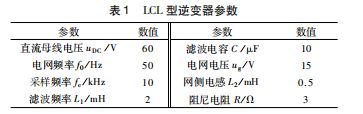
　　所有实验采用相同的逆变器模型参数，死区时间设置为200 μs，PWM 调制方式采用双极性方式，LCL 型逆变器系统参数如表1所示。

　　为验证上述PR-ADRC 控制器的有效性，搭建了如 图6所示的以TMS32OF28335 为主控芯片的实验平台， 分别对PR-ADRC 控制、传统ADRC 控制和PI 控制的LCL 型并网逆变器进行实验分析，并网逆变器参数在表1 中已经给出。在实验中，取参数kp = 2 000.ωo = 4 000. kr = 500.ω c = 75.ω 1 = 314.由于谐波主要为奇次谐波，

　　并联的谐振控制器也只包含奇次补偿器，PI 控制器的参数为p= 15.i = 0.5 。

　　3.1 动态性能的实验分析

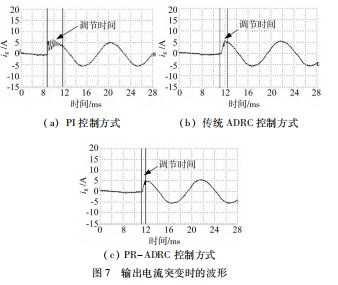
　　为验证所采用控制方法没有改变传统自抗扰快速动 态性的优势并且优于PI 控制的动态性能，使并网逆变器 工作在仅控制方式不同，其他参数均相同的情况下。当 入网电流的给定值从0A 突变至峰值5A 时，电网电流输 出波形如图7所示。

　　由图可知，PI 控制方式下，当给定值突变时大约经 过0.56 ms 的调节时间电流才能进入稳定状态;ADRC 控 制方式下，大约经过0.24 ms 并网电流便能进入稳定状 态;PR-ADRC 控制方式下，当电流突变时，仅经过 0.16 ms 就能进入稳态。可以看出，PR-ADRC 控制在电 网电流突变时依然具有良好的动态性能，具有明显的 优势。

　　3.2 电网电流谐波实验分析

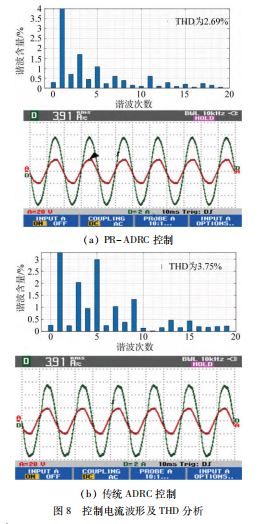
　　在并联多个谐振控制器的情况下，输出电网电流波 形如图8所示，可以看出传统PR-ADRC 控制和ADRC 控制输出的电流THD 分别为2.69% 、3.75% 。实验结果 表明PR-ADRC 控制器对谐波抑制有较好的效果。

　　4 结束语

　　为了改善并网逆变器动态性能和入网电流波形质量， 对LCL 并网逆变器设计了结构简单、参数易于调节、有 利于工程运用的降阶自抗扰控制。首先，给出了并网逆 变器传递函数，并利用Padé 近似将3阶模型等效为1阶 模型设计了并网逆变器的1 阶自抗扰控制系统。为了降 低参数调节难度，对控制器的扰动前馈通道进行了改变， 将谐振控制器加入到扩张观测器的前馈通道使其与扩张观测器的带宽参数构成比例谐振控制，以加强对并网电 流的谐波抑制效果。通过分析传递函数和伯德图，验证 了控制器的有效性，最后通过实验验证了所设计的控制 器具有较好的动态性能和谐波抑制效果。

　　参考文献：

　　[ 1 ] 张兴，李明，郭梓暄，等.新能源并网逆变器控制策略研究综述与展望[J ].全球能源互联网，2021.4 ( 5 )：506-515.
　　[2]阮新波.LCL 型并网逆变器的控制技术[M].北京：科学出版社，2015：1-15.
　　[ 3 ] LIU N，WANG J，WANG L F.Distributed energy management for interconnected operation of combined heat and power - based microgrids with demand response [ J ].Journal of Modern Power Systems and Clean Energy，2017.5 (3 )：478-488.
　　[4 ] BLAABJERG F.TEODORESCU R，LISERRE M，et al.Overview of control and grid synchronization for distributed power generation systems [ J ]. IEEE Trans on Power Electronics，2006.53 ( 5 )：1398-1409.
　　[5]鲍陈磊，阮新波，王学华，等.基于PI 调节器和电容电流反馈有源阻尼的LCL 型并网逆变器闭环参数设计[J]. 中国电机工程学报，2012.32 (25 )：133-142. [ 6 ] 杭丽君，李宾，黄龙，等.一种可再生能源并网逆变器的多谐振PR 电流控制技术[J]. 中国电机工程学报，2012.32 ( 12 )：51-58.
　　[7]徐国栋，赵庆生，梁定康，等.基于准PR 的LC 型并网逆变器双回路控制研究[J]. 电力电子技术，2021.55 ( 8 )：79-81.
　　[8]江玮，刘鸣，陈瑶琴，等.基于模糊PI 和重复控制的逆变器复合控制研究[J]. 电子器件，2020.43 ( 6 )：1273-1277.
　　[ 9 ] 赵强松，陈莎莎，周晓宇，等.用于并网逆变器谐波抑制的重复-比例复合控制器分析与设计[J]. 电工技术学报，2019.34( 24 )：5189-5198.
　　[10]邹祖冰，蔡丽娟，甘辉霞.电压型PWM 逆变器的自抗扰控制策略[J ]. 电工技术学报，2004 ( 2 )：84-88.
　　[ 11 ] CAO Y，ZHAO Q，YE Y，et al.ADRC-based current control for grid-tied inverters：Design，analysis，and verification [ J ].IEEETransactions on Industrial Electronics，2019.67 ( 10 )：8428-8437.
　　[12]王佳垚.基于改进型ADRC 光伏并网逆变器母线电压控制[ D ].天津：天津理工大学，2021.
　　[ 13 ] 马幼捷，温素娜，周雪松，等.考虑母线电压滤波的逆变器自抗扰控制器设计[J/OL]. 电测与仪表，2021-03-08.
　　[ 14 ] 马明，廖鹏，蔡雨希，等.LCL 并网逆变器的自抗扰控制策略[ J ].高电压技术，2021.47 ( 6 )：2223-2231.
　　[ 15 ] GAO Z.Scaling and bandwidth-parameterization based controller tuning [ C ]//Proceedings of the American Control Conference. Denver，Colorado：IEEE，2003：4989-4996.
 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/65259.html