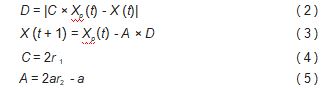SCI论文(www.lunwensci.com)
摘要:以最小化任务的最大完工时间为目标研究了具有装配约束的柔性作业车间静态调度问题, 提出了一种混合遗传灰狼算法。 在传统遗传算法的基础上进行优化, 采用基于工序和机器的双层编码方式, 工序插入式解码方法, 确保产生活动调度, 设计了基 于非线性收敛因子的灰狼算子和改进的局部搜索算子, 应用于工序交叉更新及变异操作中对机器编码二次更新, 提高了算法的局 部寻优能力并使其与全局搜索能力得到均衡 。通过对算例及实际案例进行仿真测试, 验证了算法的可行性和有效性, 对收敛速度 和寻优能力都有明显的提升。
Application of Hybrid Genetic Grey Wolf Algorithm in Assembly Constrained Shop Scheduling
Feng Miaomiao1. Cui Min1. Lü Shuqing2. Lu Zesen1
( 1. Intelligent Manufacturing Department, Wuyi University, Jiangmen, Guangdong 529020. China;
2. Guangdong Hengbao Security Technology Co., Ltd., Jiangmen, Guangdong 529700. China)
Abstract: The static scheduling problem of flexible job shop with assembly constraints is studied to minimize the maximum completion time oftasks. A hybrid genetic gray wolf algorithm is proposed. On the basis of the traditional genetic algorithm, the grey wolf operator based on thenonlinear convergence factor and the improved local search operator are designed, which are applied to the process cross update and the secondupdate of the machine code in the mutation operation, improving the local search ability of the algorithm and balancing it with the global searchability. The feasibility and effectiveness of the algorithm are verified through the simulation test of the numerical example and the actual case , and the convergence speed and optimization ability are significantly improved .
Key words: flexible workshop; genetic algorithm; grey wolf optimization algorithm; convergence factor
0 引言
在实际生产中, 尤其是复杂的定制化产品生产中, 调度问题通常含有装配工序, 要比一般作业车间调度问 题复杂得多, 不仅要考虑调度过程中的加工顺序约束, 还要考虑各工件装配工序的协调[1] 。针对具有装配约束 的柔性车间调度问题 (FJSP), 目前已有一部分学者进行 了 相 关 研 究, 采 用 遗 传 算 法 (Genetic Algorithm, GA ) 求解的占比较大 。例如, 李劲等[2]对企业的置换装配线 调度问题进行了研究, 对传统的 GA 进行了改进, 提出 了基于区域挖掘与重组的改进遗传算法, 提高了寻求到 最优解的可能性和收敛效率 。王彩虹等[3]面向定制化生 产的多产品复杂装配作业车间, 利用遗传编程的方法生 成多种组合调度规则并设计了一种改进的交叉算子, 提 高了求解算法的收敛性和鲁棒性 。马文琼等[4]通过一种 GA 和反向变邻域搜索混合智能算法对具有两阶段装配作 业方式的加工制造企业进行研究 。灰狼优化算法 (GreyWolf Optimizer, GWO ) 是根据灰狼捕食猎物活动启发而 开发的一种群智能优化算法[5] 。该算法目前已被运用于 求解 FJSP, 并取得了一定的成效 。如刘微等[6]通过将狼 群和差分算法混合, 对车间的动态问题进行了优化研究。 Lu 等[7]对离散型焊装生产车间调度问题进行研究并建立 多目标模型通过灰狼算法进行了解决 。唐红涛等[8]以最 大模糊完工时间最小为目标, 针对加工时间不确定的模 糊分布式柔性作业车间调度问题提出了一种改进的灰狼 算法 。姜天华[9]在灰狼算法基础上加入了遗传算法的交 叉变异算子以及变邻域搜索算法, 使算法的全局和局部 搜索能力得到均衡 。但是由于 GWO 提出的时间较短, 国 内目前对于 GWO 混合算法在具有装配约束的车间调度中 的应用研究依然较少 。因此, 本文将改进的 GWO 加入到 GA 中并应用于求解FJSP, 以最小化任务的最大完工时 间为目标, 提出一种混合遗传灰狼算法 ( GAGWO ), 设 计了基于非线性收敛因子的灰狼算子和改进的局部搜索算子, 进一步提高了算法求解复杂调度车间问题的性能, 并通过实验验证其有效性。
1 柔性作业车间调度问题
具有装配约束的柔性作业车间调度问题是在考虑装 配计划及装配工艺序列的基础上考虑加工的约束关系, 再确定各工件的处理顺序, 最终得到加工计划 。可以这 样描述: 车间包含 n 个工件和 m 台机器, 每个工件包含 多道加工工序, 每道工序可以在多台机器上完成加工, 其中既包含加工工序, 也包括装配工序 。本文中调度方 案是在符合工艺顺序约束和可行操作工约束的条件下, 确定工件的处理顺序, 同时使车间任务的最大完工时间为最小, 以此建立数学模型:
f = min (max (Ci )) ( 1 )
式中 Ci 为工件 i 的完工时间, i=1. 2. …, n。
需要满足的约束条件如下:
( 1 ) 所有加工设备和人员在零时刻都处于空闲状态;
( 2 ) 工序开工后不能中断;
( 3 ) 不同工件相互独立, 同一工件工序间存在工序 顺序约束;
( 4 ) 一台设备或人员在相同时间只能对一道工序进 行加工;
( 5 ) 一道工序在相同时间只能由一台设备或人员加工;
( 6 ) 同一道装配工序的所有工序全部完成才能开始 装配。
2 混合遗传灰狼优化算法设计
遗传算子包括编码 、解码 、选择 、交叉 、变异等操作, 各项操作对算法性能皆会产生重要影响 。为了提高 个体适应度, 提升在 FJSP 复杂空间寻求全局最优解的速 度以及避免陷入局部最优, 本文对传统的遗传算子进行 优化设计, 并结合灰狼算法与遗传算法, 二者优势互补, 使混合算法的整体性能更优。
2.1 染色体编码解码
( 1 ) 对于 FJSP 问题, 工件要同时选择合理且较优 的加工顺序和加工设备或人员 (统称为机器), 所以采 用双层编码方式进行编码 。一个调度方案由两层染色 体 组 成, 图 1 所 示 为 一 个 3 个 工 件 的 调 度 编 码 方 案, [ 2 1 2 3 1 3 ] 代表工件的加工顺序是[O21. O 11. O22. O31. O 12. O32], [ 4 1 2 3 4 1 ]表示当前工序在其可选择的机器集中的编号, 依次代表在可选的机器集中 选择第 4 台机器 、第 1 台机器, 以此类推。
( 2 ) 通过插入式解码方式对工序排序部分的染色体 进行解码, 并对应于机器选择部分为每个工序安排合理的机器 。解码步骤如下:
( 1 ) 通过对机器选择部分解码得到工序 Oij 的加工机 器 Mi 和时间pij;
( 2 ) 通过判断工序 Oij是不是这个机器第一道加工的 工序以及通过找到机器 Mi 上所有的间隔空闲时间段并判 断是否符合插入条件, 根据工序以及机器的具体加工情况来得到工序 Oij最早的开始加工时间。
2.2 种群初始化及选择
初始种群的质量对最优解的迭代次数 、种群规模, 以及算法的运行时间等会产生重要影响 。综合考虑机器 选择的负荷问题与机器工作负荷平衡的关系, 及初始解 在整个解空间的分散分布问题, 采用全局搜索 ( GS )、 随机搜索 ( RS ) 和局部搜索 ( LS ) 结合的方式[11], 在产 生较高质量初始种群的同时, 还可以增加种群的多样性。
选择操作的目的是避免高质量基因的损失, 锦标赛 选择方法相对于其他选择算子具有更好的收敛性 。通过 从种群中选择部分个体进行适应度比较, 将适应度较高 的个体插入到交叉池中, 从而让高性能个体以更高的几 率存活下来。
2.3 交叉操作
交叉操作决定了算法的全局搜索能力 。本文将改进 的灰狼算法嵌入 GA 的交叉操作中, 用灰狼的最优位置 更新工序编码, 而采用均匀交叉的方式更新机器编码 。
2.3. 1 工序编码更新
灰狼算法优化过程一般分为社会等级分层 、猎物追 踪 、猎物包围以及最终的狩猎阶段, 猎物追踪和狩猎过 程由种群中适应度最高的 α、β、δ三只狼引导完成 。假 设灰狼种群数目为 N, 群体的最优解 、次优解和第三优 解分别为 α、β、δ, 其他个体为 ω, 灰狼的位置更新以 及捕食行为的数学模型如下:
式中: D 为个体与其他猎物之间的距离; X 为当前灰的 狼位置; r 1 和 r2 为[0. 1]之间的随机向量; a 为收敛因子, 在迭代过程中数值由 2 线性地减小到 0.
对于每只 ω 狼, 首先根据式 ( 2 ) 计算它与 α、β、δ 的距离, 然后由式 ( 3 ) 确定灰狼向猎物移动的方向。
由灰狼算法的搜索机制可知, 变量|A|的取值影响了 狼群是扩大范围搜索猎物还是缩小范围对猎物展开攻击, 也即对算法的全局探索能力和局部寻优能力起着平衡作 用 。A 随着线性收敛因子 a 而变化, 又因线性递减的收敛 因子不能将实际的非线性收敛过程完全反映出来, 因此, 本文提出两种非线性调整策略, 分别是基于双曲正切函数规律变化和基于 sigmoid 函数规律变化的收敛因子, 在 a 从 2 递减到 0 的过程中, 二者皆满足前期收敛速度小, 后期收敛速度快的特点 。其表达式分别如式 ( 6) ~ ( 7) 所示。
式中: ainitial 、afinal 分别为 a 的初始值和终止值; t 为当前 迭代次数; Tmax 为最大迭代次数。
2.3.2 机器编码更新
机器编码更新必须确保每位基因的先后顺序不变, 因此采用均匀交叉[12]方式, 如图 2所示, 其步骤如下:
( 1) 在机器选择部分的染色体长度内随机选择一个 整数;
( 2) 在染色体长度内再随机产生与步骤 ( 1) 整数数 相同的几个互不相等的整数;
( 3) 先将父代染色体 P 1 和 P2 中几个位置的基因复制 到子代染色体 C 1 和 C2 中后, 再将 P 1 和 P2 剩下的基因也 依次交叉地复制到 C2 和 C 1 中, 复制过程保持染色体的位 置和顺序, 以此产生新的个体。
2.4 变异操作
通过简化粒子群优化算法的局部搜索, 使其代替遗 传算法的变异操作, 也即在关键路径上通过改变机器选 择, 以求完工时间最短 。机器选择的改变会使染色体原 有的某些基因发生改变, 从而使染色体产生较小的扰动 而生成新的个体 。具体做法: 在工序编码和机器编码分 别进行交叉更新后, 工序编码保持不变, 只针对最晚完工 工件的最后一道工序的机器选择进行改变, 通过改进的局 部搜索对机器编码进行二次更新, 得到更好的机器编码。 这样既保持了种群多样性, 又改善了算法局部搜索性能。
3 算法执行流程
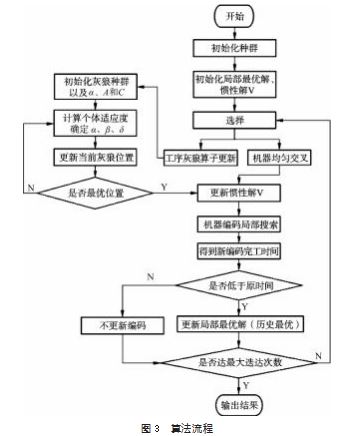
综上改进策略, 提出混合遗传灰狼优化算法的流程 如图 3所示。
其中初始化种群是设置相关参数, 初始化多个工序、 机器 、加工时间编码, 在解码得到加工时间后, 再初始 化局部最优解 、惯性解, 进而进行后续操作。
4 实验分析
混合遗传灰狼优化算法采用 Python 进行编程, 采用 的 笔 记 本 计 算 机 运 行 环 境 为 CPU i5-7200U、 主 频 2.5 GHz、 内存 4 GB、Windows10操作系统 。交叉的概率 Pc 在 ( 0.6. 0.9) 取值, 变异的概率 Pm 在 ( 0.01. 0.2) 取值, 所有测试试验中的优化目标皆为最大完工时间 最小 。
4.1 GLS不同比例设置比较实验
采用 GLR 方法, 在种群初始化的机器选择部分以 Brandimarte[13]设计的 FJSP 中的 MK01 作为算例, 对 GS、 LS 和 RS 三个参数给出不同的比例分配, 算法参数设置: 种群规模为 100. 迭代次数为 100. 变异和交叉概率为 0.1 和 0.8. 对每组的取值连续运行 10次, 实验结果如表 1所示。
MK01 算例中包含 10 个工件和 6 个机器 。从表 1 可以 看出, 不同的比例设置对算法的收敛速度和最优解都有 影响, 如果全部采用 GS 方法产生初始种群, 虽然其收敛 速度快, 但是其平均最优解最差; 结合一定的 LS 或者 RS 时, 虽然平均最优解得以改善, 但是收敛速度却受到 较大影响; 当三者都参与时, 平均最优解和收敛速度相 对均衡, 从表中数据可得, 当 GLR 的比例为 ( 0.3. 0.4. 0.3 ) 时, 实验的综合效果为最佳, 经后续实验这个参数 比例同样适用于 MK 系列其他算例。
4.2 线性和非线性收敛因子性能对比实验
同样以算例 MK01 作为例子, 验证非线性收敛因子 和线性收敛因子对算法整体性能的影响 。设置种群规模 为 100. 迭代次数为 100. GLR 采用实验 3. 1 的最佳比例 ( 0.3. 0.4. 0.3 ), 以 thx 函数和 sigmoid 函数作为非线性 收敛因子, a 为线性收敛因子, 分别连续运行 10 次, 实 验结果如表 2 所示 。从实验结果可以看出, 非线性收敛 因子相较于线性收敛因子, 函数的平均最优解和收敛速 度都有了显著优化; 对比两个非线性收敛因子, 引入 sigmoid 函数后的结果最优。
在此实验的基础上, 进一步地对用于更新工序编码 的改进灰狼算法和传统 POX 算子做仿真实验 。改进灰狼 算法的非线性收敛因子选用 sigmoid 函数, 其他参数同 上 。选用 MK02 算例运行 10 次, 实验对比结果如表 3 所 示 。从表可以看出, 用改进灰狼算法更新的工序编码, 函数能达到的最优解为 31. 优于传统的 POX 算子的最优 解, 但从平均收敛次数来看, 其收敛速度相对较慢, 整 体来讲, 工序编码用改进灰狼算法更新相比于用 POX 交 叉更新, 使得算法更稳定且解的质量更好。
4.3 算例测试与实例求解
为了验证算法性能, 选取文献[14- 16]中的测试案例进 行仿真 。此算例是一个部分柔性作业车间调度问题, 包 含 4 个工件 、6 台机器, 具体的加工信息如表 4 所示 。
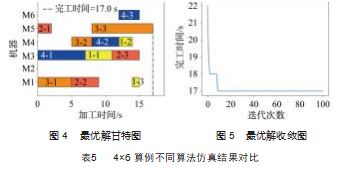
设置种群规模为 100. 迭代次数为 50. 其他参数采 用前两个实验的数据, 连续运行 20 次, 得到最优解的甘特图和收敛图分别如图 4 和图 5 所示, 表 5 为不同算法仿 真结果的对比 。从表中可以看出, 本文算法得到的最优 完工时间和其他算法区别不大, 但其平均收敛次数为 4. 明显优于其它算法, 说明本文提出的算法搜索效率高, 平均进化率为 100%, 在运行 20 次中, 每次都能找到最 优解, 说明本文算法有较高的稳定性。
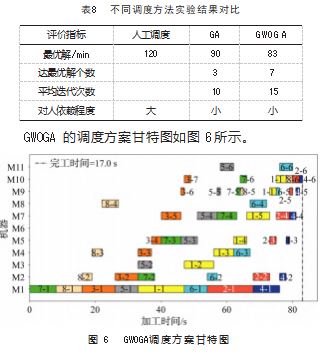
通过生产实例求解, 验证 GWOGA 算法解决实际问 题的实用性 。本文选择某五金生产加工车间 。其加工工 艺流程包括开料 、焊接 、喷粉和包装等工序, 门的装配 工艺有门框装配 、门扇装配 、门框门扇装配, 窗的装配 工艺和门相同, 因此针对不同材质门、不同产品规格的窗 进行装配工艺之前的调度, 以尽可能满足各配件同时到达 装配点的需求, 具体的产品生产加工数据如表 6 和表 7 所 示。对表中的实际生产加工数据通过分析整理, 分别采用 传统的方法以及文章提出的改进的混合算法进行调度求 解, 并将求解结果与车间实际的人工调度方法进行对比。
仿真运行 10次, 调度结果对比如表 8所示 。从表中 可以看出, 采用人工调度需要的生产加工时间长, 对人 的依赖程度相对较大, GWOGA相对于 GA虽然算法收敛 时间稍长, 但在生产任务的加工用时上却有明显的优势, 且在求得最优解时相对稳定, 在实际的生产中, 可以根 据车间生产情况选择合适的方法指导生产。
综上所述, GWOGA 在算例和实际案例的测试中都 达到了较好的效果, 说明其对求解此类问题是可行的 。
6 结束语
以最小化任务的最大完工时间为目标研究了具有装 配约束的柔性作业车间静态调度问题, 提出了一种混合 遗传灰狼算法 ( GWOGA)。 设计了一种基于非线性收敛因子的灰狼算子, 用于遗传算法交叉操作中的工序编码 更新, 并采用改进的局部搜索算子代替遗传算法的变异 操作, 对机器编码进行了二次更新, 不仅保持了种群多 样性, 局部寻优能力也得到提升, 使算法全局搜索能力 和局部寻有能力得到均衡。
通过对算例和实际案例进行仿真测试, 在收敛速度、 稳定性和寻优性等方面该算法都呈现出了良好的性能, 验证了所提出的混合算法在求解此类作业车间调度问题 中的可行性和有效性。
参考文献:
[1] 杨婷婷,吕海利,董明望,等 . 一种装配产品调度问题的粒子群 算法实现[J]. 武汉理工大学学报,2015. 37(11):93-100.
[2] 李劲,李洪,徐丽丽,等 .基于改进遗传算法的置换装配线调度 问题研究[J]. 中国管理科学,2016. 24(12):63-71.
[3] 王彩虹,韩国震,吕海利,等 .基于改进遗传编程的装配作业车 间调度研究[J]. 中国物流与采购,2017.(16):76-77.
[4] 马文琼 ,王恺 . 两阶段装配流水车间加工与配送协同调度研 [J]. 工业工程与管理,2016.21(6):103-110.
[5] Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J].Advanc ‐ es in Engineering Software,2014.69:46-61.
[6] 刘薇,蓝图,孙梓华,等 . 混合狼群算法在动态车间调度中的应 用[J]. 吉林师范大学学报,2021.42(4):66-73.
[7] Lu Chao, Gao Liang, Li Xinyu. et at. A hybrid multi-objective grey wolf optimizer for dynamic scheduling in a real-world weld ‐ ing industry[J]. Engineering Applications of Artificial Intelli ‐ gence,2017.57(1):61-79.
[8] 唐红涛,李悦,王磊 .模糊分布式柔性作业车间调度问题的求 解算法[J].华中科技大学学报,2022.50(6):81-88.
[9] 姜天华 . 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策,2018.33(3):503-508.
[10] 宋兴昌,阮景奎,王宸 .基于混合多目标遗传算法的柔性作业 车间调度问题研究[J].机电工程,2021.38(2):169-176
[11] 张国辉,吴立辉,聂黎,等 .考虑机器故障的柔性作业车间鲁棒 调度方法[J]. 系统仿真学报,2016.28(4):867-873.
[12] 斯兴瑶,廖映华,任少波,等 .基于滚动窗口技术和遗传算法的 柔性作业车间动态调度研究[J].机电工程,2022.39(1):87-93.
[13] Brandimarte P.Routing and scheduling in a flexible job shop by Tabu search[J].Annals of Operations Research,1993.41(3):157- 183.
[14] 扬晓梅,曾建潮 . 遗传算法求解柔性 job shop 调度问题[J].控 制与决策,2004.19(10):1197-1200.
[15] 王雷,邹新 .基于改进免疫克隆选择算法的柔性作业车间[J]. 南京理工大学学报:自然科学版,2018.42(3):345-351.
[16] 曹坤煜,陈永当,宋辛辛,等 . 改进免疫遗传算法求解作业车间 调度问题[J].计算机技术与发展,2020.30(11):174-179.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/64865.html