SCI论文(www.lunwensci.com)
摘要:为了有效提高多工况下地铁列车滚动轴承故障诊断精度,基于轴承振动数据,提出一种基于小波包奇异谱熵和改进鲸鱼优化 算法(IWOA ) 优化极限学习机(ELM ) 的故障诊断方法。针对轴承振动信号的非平稳性和非线性特点,采用小波包提取样本特 征,使用奇异值分解提取小波包数据集的样本信息熵,获得样本特征集。其次,针对模型参数难以确定,优化速度慢且容易陷入局 部最优问题,采用变异算子和混沌动态权重因子改进鲸鱼优化算法(WOA ),使用IWOA 优化ELM 参数获得故障诊断模型。最后, 使用美国凯斯西储大学的轴承故障数据验证了模型的可靠性和稳定性,在多工况下不同类型组合的300 组测试样本中,模型诊断准 确率为99.33% 。同时与同一数据源的其他诊断模型进行对比验证模型的优越性。结果表明,基于小波包奇异谱熵和IWOA-ELM 的 轴承故障诊断模型诊断可靠性强、准确率高。
关键词:滚动轴承,故障诊断,小波包奇异谱熵,改进鲸鱼优化算法,极限学习机
Fault Diagnosis of Train Bearing Based on Wavelet Packet
Wang Faling,Wu Jiamin,Chen Guanxiong
( Guangzhou Railway Sciences Intelligent Controls Co.,Ltd.,Guangzhou 510555.China )
Abstract:In order to effectively improve the fault diagnosis accuracy of rolling bearing of metro train under multiple working conditions,a fault
diagnosis method based on wavelet packet singular spectral entropy and improved Whale Optimization Algorithm ( IWOA ) is proposed based on
bearing vibration data.In view of the non -stationary and nonlinear characteristics of bearing vibration signals,wavelet packets are used to
extract sample features,and singular value decomposition is used to extract sample information entropy of wavelet packet data sets to obtain
sample feature sets.Secondly,as the model parameters are difficult to determine,the optimization speed is slow and easy to fall into local
optimization problems,the Whale Optimization Algorithm ( WOA ) is improved by mutation operator and chaotic dynamic weight factor,and the
fault diagnosis model is obtained by optimizing ELM parameters using IWOA.Finally,the reliability and stability of the model were verified with
the bearing fault data of Case Western Reverse University.In 300 groups of test samples with different types of combinations under multiple
working conditions,the diagnostic accuracy of the model was 99.33%.At the same time,the model is compared with other diagnostic models of
the same data source to verify the superiority of the model.The results show that the bearing fault diagnosis model based on wavelet packet
singular spectrum entropy and IWOA-ELM has high reliability and accuracy.
Key words:rolling bearing;fault diagnosis;wavelet packet singular spectral entropy;improved whale optimization algorithm;extreme learning machine
引言
滚动轴承是地铁列车的关键部件之一,对列车旋转机械的稳定安全运行起到关键作用,因此对列车滚动轴承进行健康状态监测和故障识别具有重要的意义[1-2] 。
极限学习机(Extreme Learning Machine,ELM ) 是单 效果。隐层前馈神经网络,是一种监督学习算法。与传统的分类方法对比,ELM 具有泛化能力强、鲁棒性强和学习速 度快等优点[3]。但ELM 也存在网络参数随机生成引起的 ELM,稳定性差、诊断准确率较低的问题,因此很多学者提出优化算法。宋绍楼等[4]采用改进的粒子群算法(SPSO ) 优化ELM 结合噪声自适应完备总体平均经验模态分解方 法(CEEMDAN ) 对轴承进行故障识别。王进花等[5] 提出集成ELM 实现多故障分类和识别,提高故障分类的准确性和稳定性。韩慧苗等[6]提出改进布谷鸟算法( CS ) 优化ELM 对供输弹系统进行早起故障识别,取得良好的上述文章对ELM 进行优化改进,但仍存在模型构建复杂和计算量大问题。因此本文采用改进鲸鱼算法 ( Improved Whale Optimization Algorithm,IWOA ) 优化 减少计算量的同时,有效地提高了模型的稳定性和诊断的准确率。 滚动轴承振动信号具有非平稳性和非线性特点,合 理有效地提取振动信号的特征有利于轴承的诊断分类。
小波包分解能有效地分辨非平稳信号,奇异值具有较高 的鲁棒性和稳定性,信息熵能有效地处理非线性信号。
本文将三者结合,采用小波包奇异谱熵提取轴承的振动 信号,充分反应振动信号的细节信息[7]。
基于上述分析,提出一种基于小波包奇异谱熵和 IWOA 优化ELM 的轴承故障诊断方法。使用变异因子和 混沌动态加权因子优化鲸鱼算法获得改进的鲸鱼优化算 法。针对轴承振动信号的特点,使用小波包奇异谱熵提 取轴承振动信号特征。通过改进的鲸鱼优化算法优化 ELM 的参数获得故障诊断模型。采用轴承故障数据测试 方法的有效性和可行性,最后通过对比验证确定方法的 优越性。
1 小波包奇异谱熵
1.1 小波基函数及小波包分解层数
小波包分解是可根据自身信号特点自动选择频带范 围及自动完成频带匹配的时频域分析方法[8]。
如果平方可积函数w ( t ) 的傅里叶变换w ( ω )满足:
则称w ( t ) 为一个基本小波。
选择合适的小波基函数对模型的评估结果具有决定 性的作用。根据振动信号的波形特征,本文设定小波包 分解层数为6层,小波基函数为Coiflets 3.通过对比可 知,Coiflets3 基函数的时域波形与轴承振动信号波形相似,因此选择该基函数能更加准确地反映故障信号。
1.2 小波包奇异谱熵特征提取
小波包奇异谱熵特征提取的主要步骤如下。
( 1 ) 小波包分解振动信号X ( t ),获得64 个子频带分解系数。
(2 ) 对小波包分解系数进行重构:
2 改进鲸鱼优化算法
2.1 鲸鱼优化算法
鲸鱼算法(Whale Optimization Algorithm,WOA ) 是一种新兴的、基于种群的人工智能算法。根据鲸鱼捕食猎物的行为特点将WOA 算法分为寻觅阶段和觅食阶段[9]。寻觅阶段鲸鱼个体在随机位置上游走;觅食阶段 包含两个步骤:一是通过气泡网将发现的猎物包围,二 是通过螺旋移动靠近猎物。WOA 中,猎物所处的空间位 置为方案的全局最优解,鲸鱼在移动中不断变换的位置为候选解。假设有N 个鲸鱼个体在d 维搜索空间中,则
2.2 变异算子和混沌动态权重因子
假设最优适应度值的鲸鱼个体为α。WOA 在计算随机鲸鱼个体适应度值时,算法容易陷入局部最优解[10] 。 因此为避免算法陷入局部最优解,利用变异算子对最优 个体α 进行1/D 的概率(D 为鲸鱼个体的维数)变异。 具体公式如下。
鲸鱼算法在初期经过变异操作后,为了尽快找到全 局最优解,缩短优化时间,引入混沌动态权重因子。混 沌理论能使鲸鱼个体在优化过程中遍历全局,避免陷入 局部解。而动态权重因子使得鲸鱼个体在收敛速度方面 与迭代次数成正比,提高WOA 搜索速度与精度。具体 表达式如下:
惯性权值ω ( t ) 采用混沌映射logistic 来调整,通过遍历每一个鲸鱼个体,使得所有的鲸鱼个体都能在全局 范围内搜索猎物,避免WOA 陷入局部最优解。动态收 敛因子λ的存在使得权重的变化范围得到有效控制,λ 的值随着迭代次数的增加而减小,缩小优化后期种群局部搜索的区域,加快收敛的速度。
2.3 改进鲸鱼优化算法
综上所述,采用变异算子和混沌动态权重因子优化WOA 算法。IWOA 的算法实现流程如图1所示
( 1 ) 初始化WOA 参数。设置种群规模N= 10、最大迭代次数Tmax =20.
(2 ) 随机生成鲸鱼种群,并初始化位置向量。设置适应度函数,计算目前个体适应度值,得到最优鲸鱼个体。
(3 ) 对最优个体的进行1/D 变异,根据式(9 ) 和式(10 ) 更新最优鲸鱼个体位置,重新计算当前最优适 应度值的鲸鱼个体的空间位置向量。对比适应度值并保存最优鲸鱼个体的空间位置向量。
(4 ) 随机产生(0.1 ) 的p值后,由A与p的值更新鲸鱼位置信息。
(5 ) 根据式(11 ) 对鲸鱼个体再次进行位置更新。计算更新后的鲸鱼个体的适应度值,进行比较并更新最 优解。
(6 ) 判断算法是否满足终止条件。若满足条件,则迭代终止,输出最优的鲸鱼个体位置向量。否则,返回 步骤(2 ) 继续进行迭代寻优。
3 改进鲸鱼算法优化极限学习机
3.1 ELM
ELM 网络结构由输入层、隐藏层和输出层等组成,其网络结构如图2所示。图中g (x ) 为激活函数(激活 函数采用sigmoid ),β 为权重矩阵,b i 为隐层阈值,Wi为输入权重。
3.2 IWOA-ELM 模型建立与诊断
滚动轴承故障诊断流程图如图3所示。对轴承振动 信号做预处理,获得样本集。使用小波包奇异谱熵提取 样本集的特征形成样本特征集并将其分为测试样本和训 练样本。使用改进的鲸鱼优化算法优化ELM 模型获得优 化参数,最后输入测试样本获得诊断结果。
4 实验与结果分析
4.1 试验台介绍
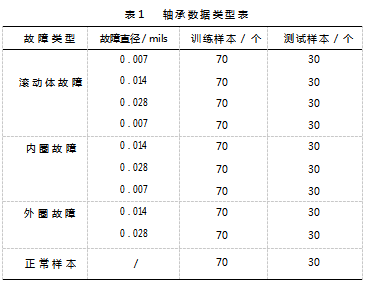
采用美国凯斯西储大学轴承数据中心提供的轴承数据[11] 。实验轴承采用电火花加工,实验平台主要由电 机、功率测试计、扭矩传感器和电子控制器等组成。实 验平台如图4所示。本文选用的数据为驱动端采集获得,实验对象为SKF 轴承,实验转速为1797 r/min,设置采样频率为48 kHz。 根据需要,设置每个样本长度为1024 个样本点。具体数 据如表1所示。
4.2 诊断结果与方法对比
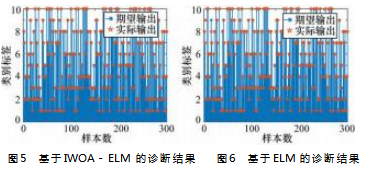
根据诊断流程,采集630 个不同故障类型样本和70 个正常样本打乱顺序组成训练样本集;采集270 个不同 故障类型样本和30 个正常样本打乱顺序组成测试样本。 将测试样本输入到训练好的模型中获得诊断结果,最终 诊断准确率为99.33% 。IWOA-ELM 模型诊断结果如图 5 所示。
为了验证IWOA 优化的有效性,采用相同特征,输 入到没有优化参数的ELM 模型获得的诊断结果如图6所 示,诊断准确率为96.67% 。
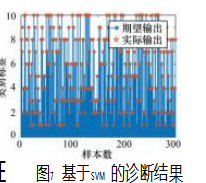
支持向量机作为小样本诊断模型经常用于故障诊断中。为了验证IWOA -ELM 的优越性,采用基于SVM 诊断模型的诊断结果如图7 所示,诊断准确率为96% 。通过对比可知,相同特征下,改进的鲸鱼优化算法优化ELM 模型在滚动轴承故障诊断方面更具有优越性。
通过与其他采用相同数据的诊断模型形成对比,验 证模型整体性能,具体结果如表2所示。由表可知,分 别对比同一数据来源下,不同特征提取方法和不同诊断 模型下,本文结合小波包奇异谱熵和IWOA-ELM 的故障 诊断模型诊断准确率最高,体现该方法的优越性。
5 结束语
( 1 ) 针对滚动轴承振动信号的非线性和非平稳性的特点,采用小波包分解结合奇异谱熵,充分获取轴承振动信号的故障信息。
(2 ) 为避免WOA 易陷入局部最优解的缺点,采用变异算子和混沌动态权重因子改进WOA,提高WOA 的 全局搜索能力和算法收敛速度。采用IWOA 优化ELM 获 得最优参数,解决了ELM 对于传统优化算法出现的收敛 速度慢、搜索能力差、容易陷入局部最优的问题,提高了模型的稳定性和诊断的准确率。
(3 ) 采用实际实验数据验证模型的可靠性和稳定性。与没有优化的ELM 模型、SVM 模型对比和其他采用 同一数据来源的文章进行对比验证,结果表明本文方法 准确率更高。
参考文献:
[ 1 ] Zhang C,Liu Y,Wan F,et al. Adaptive filtering enhancedwindowed correlated kurtosis for multiple faults diagnosis oflocomotive bearings [ J ].ISA Transactions,2020.101 (3 ) .
[2 ] 王杰,郭世伟.自适应VMD 算法在滚动轴承故障诊断方面的应用[J ].机电工程技术,2020.49 ( 11 ):161-164.
[ 3 ] 李梦瑶.基于极限学习机的旋转机械齿轮箱故障诊断研究[ D ].青岛:青岛大学,2021.
[4 ] 宋绍楼,吕亮,刘昕明.基于CEEMDAN-SPSO-ELM 的旋转 电机滚动轴承故障检测方法[J].辽宁石油化大学学报, 2022.42 ( 1 ):86-91.
[5 ] 王进花,胡佳伟,曹洁,等.基于自适应变分模态分解和集成 极限学习机的滚动轴承多故障诊[J].吉林大学学报:工学 版,2022.52 (2 ):318-329.
[6]韩慧苗,许昕,潘宏侠,等.基于模糊熵与CS-ELM 的供输弹系统早期故障识别[J ].机床与液压,2022.50 (7 ):164-169.
[7 ] 周建民,王发令,张龙,等.基于RBF 神经网络与模糊评价的 滚动轴承退化状态定量评估[J].机械设计与研究,2019.35 (6 ):116-122.
[ 8 ] Xiong S,Zhou H,He S,et al.Fault diagnosis of a rolling bearingbased on the wavelet packet transform and a deep residual networkwith lightweight multi-branch structure [ J ].Measurement Science and Technology,2021.32 (8 ):085106.
[ 9 ] XIN Z,LIU Z,QIANG M,et al.Bearing fault diagnosis using awhale optimization algorithm - optimized orthogonal matchingpursuit with a combined time - frequency atom dictionary [ J ]. Mechanical Systems & Signal Processing,2018.107 (7 ):29-42.
[10]陈志炜.基于极限学习机的轴承故障诊断研究[D].桂林: 桂林电子科技大学,2021.
[ 11 ] Piltan F,Duong B P,Kim J. Deep learning -based adaptiveneural-fuzzy structure scheme for bearing fault pattern recognitionand crack size identification [ J ].Sensors,2021.21 ( 6 ):2102.
[ 12 ] LI Y,WANG X,WU J.Fault diagnosis of rolling bearing based on permutation entropy and extreme learning machine [ C ]// 2016 Chinese Control and Decision Conference ( CCDC ).IEEE, 2016:2966-2971.
[ 13 ] 陈帅,黄晋英.基于RCMDE 与概率神经网络的滚动轴承故 障诊断[J ].制造业自动化,2022.44 (5 ):218-220.
[ 14 ] Sikder N,Arif A M,Islam M,et al.Induction Motor BearingFault Classification Using Extreme Learning Machine Based onPower Features [J ].Arabian Journal for Science and Engineering, 2021:1-17.
[ 15 ] XIAO J,ZHOU J,LI C,et al.Multi-fault classification based onthe two-stage evolutionary extreme learning machine and improvedartificial bee colony algorithm [ J ].ARCHIVE Proceedings of theInstitution of Mechanical Engineers Part C Journal ofMechanical Engineering Science 1989-1996 ( vols 203-210 ), 2013.228 ( 10 ):1797-1807.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63656.html