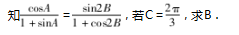SCI论文(www.lunwensci.com)
摘 要: 本文以函数类试题为切入点,通过对 2022 年高考数学试题中部分函数类试题的分析、 解答与评析,探寻同构规律,为高考数学中的函数类试题提供同构视角下的解题路径.
函数类试题作为高考中的高频考点,题型灵活 多变 ,解题方法也往往不唯一,近年来更是与导数 相结合常常坐镇高考数学的压轴地位.这类试题考 查数学抽象、逻辑推理与数学运算等基本核心素养, 试题有较好的区分度.无论试题如何变,背后通常都 有不变的元素以及解决问题的基本方法.本文从 2022 年的部分函数类试题出发,探究与分析试题背 景与命题意图,基于同构的视角探究解决该类问题 的基本做法.
所谓同构原理,就是通过观察原式的代数特征, 利用代数运算性质构造出统一 的形式( 同构的本质 是结构相同),进而构造函数,结合函数单调性直接 转化为自变量的关系,从而使形式得到很大程度的 化简.合理运用同构思想解题可以大大优化数学运 算,简化推理步骤.同构往往涉及到指对数互化、整 体换元与不等式放缩等过程,融合在比较大小、三角 函数、不等式恒成立等问题中.
1 比较大小问题
比较大小是高中数学中常见的题型,近年来考查难度也逐渐上升.这类问题通常以不等式的基本 性质为主要依据,涉及不等式、函数等多方面的数学 知识及数学思想方法,具有涉及面广、立意新、角度 新、解法灵活多样等特点,解决此类问题,需要对已 知的关系式进行观察变形得到同构关系式,构造函 数,利用函数单调性来比较大小,这类问题实质上考 查了等价转化思想,是高考考查的重点.
例 1 ( 2022 年全国甲卷文科第 12 题) 已知 9m = 10.a = 10m -11.b = 8m -9.则( ).
A.a>0 >b
B.a>b>0
C.b>a>0
D.b>0 >a
思路 1 不等式放缩.首先将 9m = 10 写成对数 形式,即 m = log9 10.与 1 作比较,再将 a 与 b 写成含 有 9m 的形式,利用 m >1 进行放缩,从而得到答案.
思路 2 同构的思想.通过观察已有的三个式 子的结构特点,将其化成同一形式,构造同构函数, 再求导,利用函数的单调性求解.
解析 此处重点阐述同构思想下的求解过程.
因为 9m = 10.所以 m = log9 10 >log9 9 = 1.
又因为 a = 10m -10 -1.b = 8m -8 -1.0 = 9m-9 -1.所以可设f( x) = xm -x -1( x >1).则f '( x) = mxm-1 -1>xm-1 -1>0.
所以f( x) 在( 1.+ ∞ ) 上单调递增.
所以f( 10) >f( 9) >f( 8).即 a>0 >b. 故选 A.
例 2 ( 2022 年 新 高 考 Ⅰ 卷 第 7 题) 设 a =
思路 2 同构法,仍然是两两比较的思路,通过 对 a,c 和 b,c 作差,构造恰当的同构函数利用单调 性比较出大小,而对 a,b,通过同时扩大到原来的 9 倍,再观察出特征直接构造同构函数,利用单调性比出大小.
思路 3 泰勒公式法.对 ex 与 ln( 1 + x) 通过泰 勒公式进行有限项的展开,计算出 a,c 的近似值,再 与 b 进行比较,即可比较出三者大小.
解析 此处阐述同构的方法.
评析 从同构法的思路来看,将 a,b,c 进行两 两比较时,只需稍加观察和变形,构造出同构式再进 行作差,利用函数单调性可得到大小关系.
2 三角函数问题
三角函数是高考的必考题型之一,属于中档题. 此类问题的情境创设通常简单新颖,设置方式多种 多样,难度适中.由于三角公式众多,因此往往切入 点不唯一,破解方法多种,对各层次学生能力的考查 都有一定的体现,可以很好地考查学生的数学运算 与逻辑推理能力,解决此类问题,除了从诱导公式入 手,还可以通过观察,巧妙地将原式转化成同构式, 构造函数,利用单调性求解.
例 3 ( 2022 年新高考 Ⅰ 卷第 18 题第( 1) 问) 记△ABC 的内角为 A,B,C 的对边分别为 a,b,c,已
思路 1 对原等式进行变形,将等式右边用二 倍角公 式 进 行 转 化,最 后 用 两 角 和 差 公 式 得 到 cos( A + B) = sinB,最后根据 C 的范围确定 sinB,由 此求出 B.
思路 2 利用同构思想,将等式两边构造成同 一形式,利用同构函数及其单调性,得出 A,B 的关 系,进而求解.
解析 此处阐述同构法,原式可写成
评析 本题的巧妙之处在于,题目给的等式是 长得很像的,因此可以考虑构造同构方程,根据 sinA 与 cosA,sin2B 与 cos2B 的关系,可以用同角三角函 数的基本关系进行替换,因而不难构造出同构式,从 而构造函数,利用函数单调性得到自变量之间的关 系,从而再利用诱导公式以及三角关系进行转化.
3 不等式的恒成立问题
函数大题是高考必考题之一,并且往往与导数 结合作为压轴题出现,属于难题,当中就有一类不等 式恒成立问题,若采取常规方法处理,则会呈现运算 量大,变形复杂等特点,此时若能通过合理变形,采 用同构策略,则可以迅速化繁为简,揭示问题本质.
例 4 ( 2022 年全国甲卷理科第 21 题第( 1 )
思路 1 直接对原函数求导,根据导数确定函 数单调性及最值求解.
思路 2 通过构造同构函数,换元,再根据导数 确定单调性,求解.
解析 此处重点阐述同构的方法.
可知当 x ∈ ( 0.1 ) 时 t'<0.t 单调递减,x ∈ ( 1. + ∞ ) 时 t'>0.t 单调递增,x = 1 时 t' = 0.因此 x = 1 时有 tmin = 1.
又因为 et + t≥a,令 q( t) = et + t( t≥1) , 求导有 q'( t) = et + 1>0.
所以 q( t) 在[ 1.+ ∞ ) 上单调递增.
于是有 q ( t) min = q( 1) = e + 1.所以 a≤e + 1.
点拨 解决不等式恒成立问题主要有三个基本 思路,一是通过研究函数的单调性确定函数在给定 区间上的取值范围; 二是将不等式拆分成两部分, 分别求其最大值与最小值进行比较; 三是利用同构 思想合理使用切线放缩进行证明.
通过上述例题,不难发现,同构视角下函数类试 题的处理策略,可概括为三点: ( 1) 通过观察与变形 构造同构式; ( 2) 利用函数的性质解题; ( 3) 根据题意, 进行解答.虽然看起来过程比较清晰简单,但是真正要 使用同构进行解题,需要学生熟练、灵活地掌握代数运 算性质,并能够对题目所给的式子进行观察,根据个人 的做题情况进行归类与整理,形成同构的独到视角,那么同构的方法将会是高考数学解题的一大利器.
参考文献:
[1] 唐明超,潘敬贞,袁锦前.例谈同构视角下函数与导数高考试题的求解策略———从 2020 年高考试 题谈起[J].中学数学研究,2021( 05) : 45-47.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/62940.html