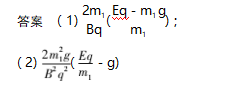SCI论文(www.lunwensci.com)
摘 要: 本文以多角度对 2022 年高考全国甲卷第 18 题带电粒子在复合场中运动轨迹的问题 进行分析,探讨粒子在运动过程中的两个最值,进行拓展与变式应用.
复合场是指电场、磁场、重力场中的两种或三种 场的叠加.关于带电粒子或带电质点在复合场中的 运动,中学阶段一般讨论的是匀速直线运动、匀速圆 周运动或类抛体运动等特殊情况.对于带电粒子在 复合场中做一般的曲线运动,往往由于知识缺陷或 思维障碍很少讨论曲线的性质.本文对 2022 年全国 甲卷第 18 题关于带电粒子在复合场中运动轨迹的 问题进行研究,拓展并深化带电粒子在复合场中做 一般的曲线运动问题.
1 试题与问题
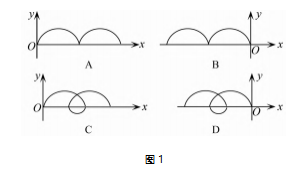
题目 ( 2022 全国甲卷第 18 题) 空间存在着匀 强磁场和匀强电场,磁场的方向垂直于纸面( xOy 平 面) 向里,电场的方向沿 y 轴正方向.一带正电的粒 子在电场和磁场的作用下,从坐标原点 O 由静止开 始运动.下列四幅图中,可能正确描述该粒子运动轨 迹的是( ).
答案解析 在 xOy 平面内电场的方向沿 y 轴正 方向,在坐标原点 O 静止的带正电粒子在电场力作 用下会向 y 轴正方向运动.磁场方向垂直于纸面向 里,根据左手定则知,向 y 轴正方向运动的带正电的 粒子会受到沿x 轴负方向的洛伦兹力,故带电粒子向 x 轴负方向偏转,选项 A、C 错误; 运动的过程中 在电场力对带电粒子做功,粒子速度大小发生变化, 粒子受的洛伦兹力方向始终与速度方向垂直,洛伦 兹力不做功.当粒子从开始运动到再次运动到 x 轴 时,电场力做功为零,粒子再次回到 x 轴时的速度为 零,然后又重复向左偏转,选项 B 正确、D 错误.
有关带电粒子在复合场中做一般曲线运动的问 题,在一些新高考地区的高考中出现的频率较高,如 往年的江苏卷、山东卷、重庆卷等曾多次出现,今年 的广东卷第 8 题也出现此类问题.
2 轨迹研究
在以上全国卷甲第 18 题中,设匀强磁场的磁感 应强度大小为 B,方向垂直于 xOy 平面向里; 匀强电 场的场强大小为 E,方向沿 y 轴正方向; 带正电粒子的质量为 m,电荷量为 q( q>0).
定性分析 1 如图 2 所示,设粒子速度为 v,沿 x 轴负方向的速度为 vx 时,洛伦兹力沿 y 轴向下的分 量大小满足 Bqvx = Eq,此时粒子继续向左上方运 动.由于洛伦兹力不做功,由动能定理可知粒子运动 到最高点时电场力做功最大,此时粒子的速度最大. 可知粒子在最高点受到竖直向下的洛伦兹力大于电 场力,粒子又会从最高点向左下方运动,由动能定理 知粒子运动到与释放点等高处即 x 轴上时其速度为 零,然后粒子又重复开始运动; 可知粒子运动轨迹的 情况大致如题给出的选项 B 所示.
力相平衡,粒子参与一个沿水平向左速度为 v0 的匀 速直线运动; 水平向右的速度 v0 使粒子参与一个在 xOy 平面内以释放点的水平线( 即 x 轴) 为切线且沿 顺时针方向的匀速圆周运动; 故带电粒子的的运动 可视为以上两个运动的合成,其轨迹曲线为摆线,即 沿水平方向做匀速直线运动的车轮边缘上某点的运 动轨迹.
定量分析 如图 4 所示,粒子从坐标原点 O 处 开始运动,设 t 时刻粒子的速度为 v,其水平分速与竖直分速分别为vx 、vy,由牛顿第二定律有:
以上第( 10) 、( 11) 式即为粒子运动轨迹曲线的 参数方程,由数学知识得,这种曲线为摆线.
3 问题拓展
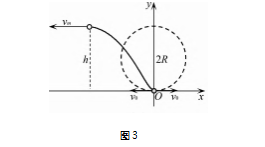
在以上粒子运动轨迹研究的基础上,求粒子运 动过程中的最大速度 vm 大小及向上运动( 离 x 轴) 的最大距离 h.
方法 3 如图 2 所示,将粒子在某一时刻的速 度 v 分解为水平速度 vx 和竖直速度 vy,其水平分速 vx 产生的洛伦兹力沿 y 轴向下,竖直分速 vy 产生的 洛伦兹力水平向左.将粒子从释放运动到最高点的 过程分成很多小微小单元,由动量定理可知,此过程中粒 子 在 水 平 方 向 上 的 动 量 改 变 为: - mvm = -ΣBqvyΔt = -BqΣvyΔt = -Bqh;
4 变式应用
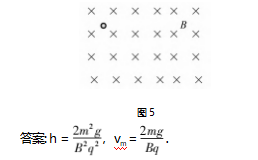
若质量为 m、电荷量为 q 的带电的小球从磁感 应强度大小为 B 的足够大的匀强磁场中静止释放 ( 如图 5 所示),求小球下降的最高度 h 与小球运动的最大速率vm.
应用 如图 6.两极板间存在磁感应强度为 B 的匀强磁场,静止在负极板附近的带负电微粒质量 为 m1 、电量为-q,在 MN 间突然加上匀强电场 E 时 开始运动,水平击中速度为零的中性粒子 m2 后,粘 合在一起恰好沿一段圆弧运动到 N 极板上,求
( 1) m1 击中 m2 时的高度 h1 及 m1 击中 m2 前瞬 时速度大小v1 ;
( 2) m2 的质量及 m1 和 m2 粘合体做圆弧运动的 半径 R.
如果复合场是匀强电场、磁场、重力场三种场的 叠加,可以将重力场与电场合成一个“等效场”,求 出“等效重力加速度”,我们仍然可以用动能定理与 动量定理、运动的合成与分解、一元二次方程根的判 别式等方法,分析求解带电粒子在复合场中做一般曲线运动的相关问题,也可将以上结论迁移应用.
参考文献:
[1] 许文.对一道原创试题的一点探讨 [J].中学物理,2019( 04) : 51-52.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63068.html