SCI论文(www.lunwensci.com)
摘要:为提高效率, 解决手工研磨、电火花拷贝、电解加工等方法在航空发动机叶片前后缘加工过程中存在的种种问题, 提出了 一种六轴电火花包络加工方法对叶片前后缘进行修整。因电极制造、安装过程中会引入多项误差, 为最大程度降低成本, 制订合 理化的公差约束, 对 UG 进行二次开发, 在不考虑放电间隙与电极损耗的情况下, 按 6 级公差等级对已有的电极模型施加 6 个自由 度方向的单项源误差和 57 种组合源误差。根据共轭曲面啮合理论, 分析各源误差对最终包络加工误差的影响规律, 得到此新工艺 中需严格控制的误差敏感因素。结果表明: 在其他条件相同时, 单项源误差 δz 、δ C 的误差扩大倍数 K 分别为1.15 和 1.61. 对包络加 工误差影响较小; 组合源误差 δxB 、δyA 的误差扩大倍数为 10.46 和 8.53. 对包络加工误差影响较大, 应严格控制。
关键词:敏度分析,六轴数控加工,包络,电火花
Error Sensitivity Analysis of Six-axis EDM Envelope Dressing of Blade Leading and Trailing Edges
Li Zheng, Cao Lixin, Yu Zuyuan
(School of Mechanical Engineering, Dalian University of Technology, Dalian, Liaoning 116024. China)
Abstract: In order to improve efficiency and solve various problems in the process of machining the leading and trailing edges of aero-engine blades by manual grinding, EDM copying and electrolytic machining, a six-axis EDM envelope machining method was proposed to trim the leading and trailing edges of the blades. There would be several errors in the electrode manufacturing and installation process . In order to minimize the cost and develop a rationalized tolerance constraint, a second development of UG was carried out, and single source errors and 57 combined source errors in 6 degrees of freedom directions were imposed on the existing electrode model according to 6 tolerance levels without considering the discharge gap and electrode loss. According to the engagement principle of the conjugate surface, the influence law of each source error on the final envelope processing error was analyzed, and the error sensitive factors that need to be strictly controlled in this new process were obtained. The results show that the single source errors δz and δ C have the error expansion multiplier K of 1. 15 and 1.61.respectively, which have less influence on the envelope processing error; the combined source errors δxB and δyA have the error expansion multiplier of 10.46 and 8.53. which have more influence on the envelope processing error and should be strictly controlled .
Key words: sensitivity analysis; six-axis CNC machining; envelope; EDM
0 引言
叶片是航空发动机的基础、核心零部件。叶片前后 缘具有厚度薄、半径轮廓小、曲率变化剧烈等特点, 对 发动机性能起着重要作用, 其加工一直是叶片制造的难 点。本文为解决铣削加手工研磨[1-2]、电解加工[3-4]、电 火花拷贝加工[5-8]等方法在前后缘的加工过程中存在的效 率低下、精度不达标以及无法脱模等问题, 提出一种六 轴电火花单参数包络加工方法对叶片前后缘进行修整, 以提高效率、解决上述问题。其基本原理为: 根据共轭 曲面啮合原理, 用复杂曲面电极线接触包络加工叶片边 缘曲面, 此方法需要用 6 个自由度才能描述电极相对叶 片的姿态。具体加工原理本文不予讨论。另外, 此工艺 需搭建有六轴联动功能的专用加工中心进行试验[9- 10]。
影响此工艺加工精度的因素繁多, 前期工作已对此 工艺几何原理的正确性进行了验证, 分析了刀位点密度、 电极设计与建模误差等因素对最终加工精度的影响。本 文主要从几何原理上对此工艺的误差敏感因素进行仿真 分析。因在电极制造、安装过程中涉及多项误差, 电极 模型与运动轨迹相对复杂, 难以建立数学模型, 所以这 些源误差对包络误差的影响难以直观评估。以往公差的 制订都是根据经验进行, 并无可靠依据, 为最大程度降 低试验成本, 以较宽松的公差要求获得满足精度要求的 试件, 本文对 UG 进行二次开发, 以前缘加工为例, 对 电极工作曲面施加 6 个自由度方向的单项源误差和 57 种 组合源误差, 这些误差既可看作电极制造误差, 又可视 作安装误差, 两者等价。利用共轭曲面啮合原理求出电极存在制造、安装误差情况下的电极运动包络面点云数 据, 分析了各源误差对最终包络加工误差的影响。为电 极制造、安装, 试验机床的搭建等过程中所涉各项公差 的制订提供了参考。
需说明的是, 本文主要从几何原理上进行仿真分析, 并未考虑放电间隙和电极损耗的影响, 这些因素的影响 可在后续实验的基础上, 对所设计的电极曲面和运动位 姿进行修形或补偿, 此处不予考虑。
1 电极、叶片模型与包络加工过程简述
1.1 电极与叶片模型
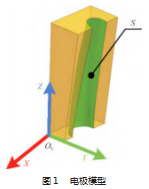
电极模型如图 1 所示, 曲面 S 为电极工作曲面, OE XYZ 为电极坐标系, 定义了电极相互垂直的 3 个定位 表面, 用于描述电极在工件坐标系中的位置和姿态, 下 文用{OE }表示。图 2 所示为叶片截面示意图, 虚线为中弧线, 弦长 b 为中弧线与前后缘交点的连线, 也即截面内相距最远两 点的连线。叶片前后缘一般定义为距弦长端点 3~5 mm 内 的部分, 尺寸 a 1 、a2 所定义部分分别代表了叶片前缘和 后缘。根据此定义, 取 a 1 = a2 = 3 mm, 对叶片区域的划 分如图 3 所示。
1.2 包络加工过程简述
实际加工中, 6 个自由度的运动由电极和叶片共同 完成。而从几何原理上对误差敏感因素进行仿真分析只 需进行刀轨仿真。故本文中, 6 个自由度的运动由电极 单独完成。
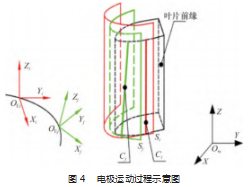
理想情况下, 电极沿刀位轨迹进行六轴运动, 且在 每一刀位点处始终保持工作曲面与叶片边缘曲面有一条 接触线。图 4 为电极运动过程示意。其中, 体 1 为叶片前缘; OW XYZ 为工件坐标系, 下文用{OW }表示; 曲线 a 代 表电极坐标系原点 OE 在工件坐标系{OW }中的运动轨迹, 电极沿轨迹 a 运动过程中, 电极坐标系{OE }在工件坐标系 {OW }中的分量也随之变化。为描述方便, 将电极模型简 化为由电极坐标系与电极工作曲面表示, 坐标系 { OEi }、 曲面 Si 描述第 i 个刀位点处电极相对叶片前缘的位置, Ci 表示电极工作曲面 Si 与叶片前缘的接触线, 第 j 个刀位点 同上。当刀位点足够密集时, 就可包络出叶片前缘形状。
2 电极运动包络面点云及其误差的求解
理想情况下, 电极沿刀位轨迹运动后, 工作曲面形 成的包络面与叶片应完全吻合。但因各种因素的影响, 包络面相对叶片前缘曲面总是存在一定的误差。电极的 设计、建模误差、刀位点密度等因素对包络误差的影响 已在前期工作中完成仿真分析。本章给出了理想情况下 和电极制造安装存在误差情况下包络面点云及其误差的 求解方法, 以便对因电极制造、安装误差所引起的包络 加工误差进行分析。
2.1 理想状态下包络面点云的计算
由图 4 可知, 理想情况下, 电极工作曲面 S:r ( u, v )沿刀位点运动形成的单参数曲面族{ St }可用矢量方程表示:
{St }:R = R (u, v ; t) ( 1 )
式中: t 为曲面族的参数, 每给 t 一个值, 矢量方程 (1) 就代表一个曲面 St, 当 t 变化时, 曲面 St 就随之变化;u, v 为 St 上的参数。
设曲面族 {St } 的包络面, 也即电极工作曲面运动的 包络面为 Σ, 则 Σ 的每一点都属于{St } 中的唯一一个曲面St, 且和 St 在该点相切。由图 4 知, Σ可由每时刻电极工作曲面与叶片前缘接触线 Ct 的总和表示:
Σ (t) = Ct0 ∪ Ct 1 ∪ … ∪ Ctm ( 2 )
式中: t 为刀位点序列; t0 、tm 为起始和结束点位。
设点 P0 为接触线 Ct0 上一点, 则其应满足经典啮合 条件:
VP0•nP0 = 0 ( 3 )
式中: VP0 为点 P0 相对于包络面的相对运动速度; nP0 为 曲面 St0 上点 P0 处的法向单位矢量; 刀位点足够密集时, VP0 可根据 St0 与 St 1 由差分代替微分求出, nP0 可调用 UG 函数求得。
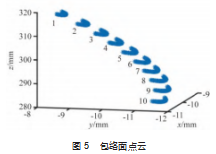
综上, 可在 St0 上生成 n 条与接触线 Ct0 垂直的参数 线, 根据 St0 与 St 1 信息, 在每条参数线上用二分法搜索满 足式 (3) 的点, 这些点即为接触线 Ct0 上的点。同理, 由曲面族 { St } 可求出所有刀位点处的电极曲面与叶片前 缘的接触线 Cti, 其中 0 ≤ i ≤ m - 1.刀位点个数 m=60. 参数线条数 n=10 时, 求得的电 极工作曲面运动包络面点云如图 5 所示。
2.2 存在源误差情况下包络面点云的计算
参考工业机器人的坐标系描述方法[13], 在电极存在 制造、安装误差情况下, 电极工作曲面沿刀位轨迹运动 形成的曲面族 { Sδt }在工件坐标系{OW }中可表示为:
{ Sδt } : Rδ ( u, v ; t) = E(w)T ( t)• E(E)δ Tu • E r ( u, v)
式中: E(w)T ( t) 、 E(E)δ Tu 均为 4×4 的齐次变换矩阵, E(w)T ( t) 为t 时刻电极坐标系{OE }相对工件坐标系{OW }的变换矩阵, E(E)δ Tu 为电极工作曲面 S 从电极理想坐标系{OE }到误差坐标系的变换矩阵, u 为误差种类; E r ( u, v) 为电极工作曲 面 S 在电极坐标系{OE }中的位置。
当引入的源误差值确定时, 根据式 (4) 可在 UG 平台上得到曲面族 {Sδt } 的模型。同 2.1 节所述, 利用曲面Sδt0 与 Sδt 1 可得到 Sδt0 与包络面 Σδ 的切线上的离散点, 同 理, 刀位点足够密集时, 可由{ Sδt } 求出存在误差时电极 工作曲面 Sδ 运动包络面 Σδ 的点云。得到电极工作曲面运 动包络面的点云数据后, 调用 UG 函数, 即可求得点云 中各点距叶片前缘的最短距离, 此距离即为各点处的误 差值。
3 电极制造误差对叶片边缘包络加工精度的影响
由前期工作知: 当刀位点个数 m 达到 60 时, 包络面 上的最大误差降低到极限。故本章以刀位点个数 m=60 为 例, 对 电 极 进 行 1: 1 建 模, 电 极 块 尺 寸 为 20 mm × 15 mm × 44 mm, 根据 6 级公差等级[11- 12]对电极工作曲面 施加尺寸与转角源误差, 各项源误差值如表 1 所示。表中, δx 为电极工作曲面整体沿电极坐标系 XOE 轴负方向偏 移的源误差值; δy 、δz 分别为电极工作曲面整体沿电极坐 标系 YOE 、ZOE 轴正方向偏移的源误差值; δA 、δB 、δ C 分别为电极工作曲面绕 XO 、YO 、ZO 轴顺时针旋转的转角源误差。
源误差对包络误差的影响程度用误差扩大倍数 K来 表示:
式中: ε u 为存在 u 类误差时包络面上的最大误差值; ε 0 为无源误差时包络面上的最大误差值。
3.1 单项源误差仿真分析
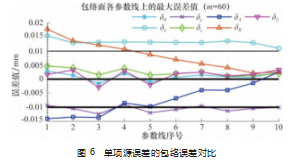
为得到单项源误差对包络误差的影响规律, 对电极 模型分别施加 6 个自由度的单项源误差, 求出电极工作 曲面运动的包络误差, 与无源误差时的包络误差形成对 比。误差对比如图 6 所示。
包络面最大误差 ε u ( m ) 与误差扩大倍数 Ku ( m ) 如表 2 所 示。分析图 6 与表 2 可知, 除 δz 、δ C 对包络误差的影响较 小外, 其余 4 种单项源误差对包络误差的影响均较大。
3.2 组合源误差仿真分析
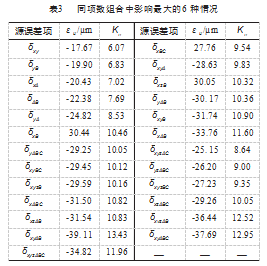
为最大程度降低成本, 本节对 6 个自由度方向的源误差进行共 57(C )种不同的组合, 以期发现对包络加6(i)工精度影响最大的源误差组合。再对影响较大的源误差 组合进行方向上的变化, 判断组合源误差之间是否存在 可以相互抵消的情况, 从而尽可能地制订宽松的公差要 求。因篇幅限制, 相同项数的组合只列出了影响最大的 6 种情况。表 3 中, δxy 表示对电极工作曲面同时施加 δx 和 δy 源误差, 其他变量的含义依此类推。分析表 2、表 3 知: δxB 、δyA 的存在对包络加工误差的影响较大; δz 、δ C 的存在可抵消部分 δxB 、δyA 对包络误差的影响。
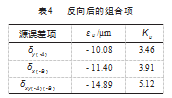
为探究 XO 方向尺寸误差与绕 YO 的转角误差、 YO 方向的尺寸误差与绕 XO 的转角误差是否可以实现部分抵消, 对电极曲面施加 δx ( -B ) 、δy ( -A) 、δxy ( -A) ( -B ) 源误差进行误差仿真分析, -A、-B表示电极工作曲面分别绕 XO 、YO轴逆时针旋转, 结果如表 4 所示。由表 3、表 4 可知, δy 与 δ( -A) 同时存在可抵消部分各自对包络加工误差的影 响; δx 与 δ( -B ) 同时存在可抵消部分各自对包络加工误差 的影响。
4 结束语
本文对 UG 进行二次开发, 在不考虑放电间隙与电 极损耗情况下, 从几何原理入手, 分析了电极制造误差 对叶片边缘包络加工精度的影响, 电极安装误差对精度 的影响与电极制造误差等价。得到以下结论。
( 1) 单项源误差中, δz 、δ C 对包络误差影响较小, 可制订适当宽松的公差约束。
( 2 ) 57 种组合源误差中, δxB 、δyA 的误差扩大倍数分 别为 10.46 、8.53. 对包络误差影响很大, 在公差制订中 应严格控制, 避免出现此类组合的源误差。
( 3 ) δx ( -B ) 、δy ( -A) 的误差扩大倍数分别为 3.91 、3.46. 即 δx 与 δ( -B ) 、δy 与 δ( -A) 可相互抵消一部分各自对包络误差 的影响。应尽量按照此类组合进行公差的制订。
参考文献:
[1] 李海宁,赵赟, 史耀耀,等 . 航空发动机风扇/压气机叶片制造关 键技术[J]. 航空制造技术, 2013 (16): 34-37.
[2] 张海艳, 张连锋 . 航空发动机整体叶盘制造技术国内外发展概 述[J]. 航空制造技术, 2013(Z2): 38-41.
[3] 张明岐, 张志金,黄明涛 . 航空发动机压气机整体叶盘电解加 工技术[J]. 航空制造技术, 2016(21): 86-92.
[4] 吴建民,徐家文 . 整体叶轮数控展成电解加工运动轨迹及速度 研究[J]. 机械科学与技术, 2008(8): 1089- 1091.
[5] Xi X C, Liu H D, Chen H, et al. Kinematics for a six-axis EDM machine by screw theory and its application in feedrate planning in EDM for shrouded blisks[J]. International Journal of Advanced Manufacturing Technology, 2019. 105(3):1- 11.
[6] 田喜明, 张云鹏, 陈阳 . 带冠整体叶轮电火花加工电极结构与 运动轨迹设计方法[J]. 电加工与模具, 2019(1): 12- 15.
[7] Liu X, Wei L, Kang X, et al. Electrode Feed Path Planning for Multi-axis EDM of Integral Shrouded Impeller[J]. The Interna⁃ tional Journal of Advanced Manufacturing Technology, 2013(68): 1697- 1706.
[8] I Ayesta, B Izquierdo, J A Sanchez, et al. Optimum electrode path generation for EDM manufacturing of aerospace components [J]. Robotics and Computer Integrated Manufacturing, 2016(37): 273-281.
[9] 龙金, 宋涛, 闫步云,等 . GH4169 航空发动机叶片的电火花修整 工艺参数优化研究[J]. 电加工与模具, 2021(3): 23-30.
[10] 宋涛,龙金, 闫步云,等 . 振动辅助电火花修整航空发动机叶片 进排气边误差工艺参数优化及对比[J]. 航空制造技术, 2020. 63(4): 48-53.
[11] GB/T 1800. 1—2009. 产品几何技术规范(GPS), 极限与配合[S]. [12] GB/T 1184— 1996. 形状和位置公差[S].
[13] [美] Saeed B. Nuku 著 . 机器人学导论— 分析、控制及应用 (第二版)[M]. 孙富春, 朱纪洪, 刘国栋, 等译 . 北京 : 电子工业 出版社, 2018.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/58274.html