SCI论文(www.lunwensci.com)
摘要: 为进一步提高井下原位测量装置推靠机构的传动性能, 采用复数矢量法建立了井下原位测量装置推靠机构的数学分析模型, 推导出了各构件的位置方程 、速度方程及加速度方程, 并在运动学分析解得各部件的加速度的基础上又进行了各部件的动态静力学分析, 得到推靠系统各杆件运动参数, 真实反映推靠系统的实际运动状况。通过 MATLAB 建立推靠机构数学分析模型, 得出该模型运动学特性理论变化曲线, 当 θ1=29.3°时, 推靠机构推靠杆推靠最大行程达到 257 mm。基于 ADAMS 仿真平台, 建立了推靠机构的运动学仿真模型, 并进行了运动学分析。将得到仿真分析结果与数学分析模型进行对比, 验证了所建立的井下原位测量装置推 靠机构运动学数值分析模型与运动学仿真分析的正确性, 为井下原位测量装置推靠机构的优化设计提供了依据。
关键词: 井下原位测量装置,复数矢量法,运动学,推靠机构,ADAMS
Dynamic Analysis and Simulation of the Downhole in Situ MeasuringDevice Push-back System
Bai Baoxin, Wu Wei, Zhang Jianwei, Wang Jinchao
(College of Mechanical Engineering,Xi′an Shiyou University,Xi′an 710065.China )
Abstract:In order to further improve the transmission performance of the push mechanism of the downhole in-situ measurement device,the mathematical analysis model of the push mechanism of the downhole in-situ measurement device was established by using the complex vector method,the position equation,velocity equation and acceleration equation of each component were derived,and the dynamic static analysis of each component was carried out on the basis of the kinematics analysis to obtain the acceleration of each component,and the motion parameters of each member of the push system were obtained,the actual motion of the pushing system was truly reflected.The mathematical analysis model of the pusher mechanism was established through MATLAB,and the theoretical variation curve of the kinematic characteristics of the model was obtained.When θ1= 29.3°,the maximum stroke of the push rod of the push mechanism reached 257 mm.Based on ADAMS simulation platform,the kinematics simulation model of the push mechanism was established,and the kinematics analysis was carried out.The simulation analysis results are compared with the mathematical analysis model,which verifies the correctness of the established kinematics numeric alanalysis model and kinematics simulation analysis of the pushing mechanism of the downhole in-situ measuring device,and provides a basis for the optimization design of the pushing mechanism of the downhole in-situ measuring device.
Key words:downhole in situ measurement device;complex vector method;kinematics;pushing mechanism;ADAMS
0 引言
“井下原位测量装置”作为同时满足井壁取芯 、岩 心测量和流体测量条件的新型地层信息勘测方法逐渐被 国内外各大能源服务公司采用并研究[1] 。 目前, 关于井 下原位测量装置推靠机构的运动学及动力学分析方面的 研究较少, 缺乏详细的理论分析模型, 因而无法准确描 述井下测量装置推靠系统的真实的运动状态和运动规律。 文献 [2] 利用复数矢量法进行新型分动式六臂井径测 井仪推靠系统运动学及动力学分析, 得到了该测井仪推 靠机构各杆件的位置方程 、速度方程及加速度方程; 文 献 [3] 用矩阵解析法对微电阻率扫描测井仪极板推靠 机构运动学进行分析, 从而得到该测井仪推靠机构各杆 件运动参数, 真实反映推靠机构的实际运动状况。
推靠机构运动性能的好坏直接影响取芯效率及测井 数据的准确性[4] 。本文就井下原位测量装置推靠机构运 动学及动力学进行研究, 运用复数矢量法得到井下原位 测量装置推靠机构各杆件的位置方程 、速度方程及加速 度方程, 并对各杆件进行动态静力学分析得到了动态静 力学方程; 通过 MATLAB 建立推靠机构数学分析模型, 得出该模型运动学特性理论变化曲线; 运用 Adams 对井 下原位测量装置推靠机构进行虚拟样机建模和运动仿真, 进一步分析了其运动规律, 有助于在地层信息勘探中实 现输出运动的最大精度, 为后续推靠机构动力学分析及 结构参数优化提供了理论依据[5] 。
1 井下原位测量装置推靠机构物理模型建立
本文设计的井下原位测量装置三维图如图 1 所示,推靠范围为 140 ~ 257 mm, 提供的推靠力为 2 ×100 kg。 推靠机构结构如图 2 所示, 由推靠臂 、推靠板 、推靠辅 助臂 、推靠液压缸组成。推靠模块分别由液压缸 6 、13 提供动力, 辅助臂 1 、推靠板 2 、推靠臂 3 组成曲柄连杆 机构, 同样推靠臂 7 、推靠板 8 、辅助臂 9 也组成曲柄连 杆机构。当推靠液压缸 6 、13 的液压活塞杆推出时, 通 过推靠臂 3 、7 分别作用在曲柄连杆机构上, 使得推靠板 2 、8 从仪器上打开并将井壁取芯测量装置推靠在井段侧 壁上。当推靠液压缸不断提供压力作用在推靠板上时, 仪器取芯口一侧得以牢靠紧密贴合井壁为后续取芯测量 工作奠定工作基础。当推靠液压缸活塞杆回退时就可以 把推靠板收回到仪器上, 并能够和仪器外壳完全贴合。 由于该机构采用两个液压缸分别对两个推靠板提供动力, 故在环境复杂的裸井环境中, 通过调节两个液压缸的油 量供给以使各推靠板能够贴合不同的井段侧壁, 从而使 整个仪器能够保持合适的姿态进行作业。
2 推靠机构工作过程力学分析
当仪器下放至指定深度时, 推靠活塞伸出, 使仪器 紧贴在井壁, 用以进行钻进取芯及后续工作。将推靠活 塞合理设置在钻头两侧 ( 仪器上端与下端各一个), 双 点推靠使仪器钻头钻进面紧贴井壁进行钻进取芯 、探头 测试, 整个钻进测试过程中仪器推靠牢固, 仪器不偏移 不偏转。在此机构中, 构件个数为 4. 移动副个数为 1. 滚滑副个数为 4 。并且, 机构中存在 1 个虚约束, 故机构的自由度数为 1. 即推靠机构具有确定运动[6] 。
2.1 推靠机构工作过程运动学分析
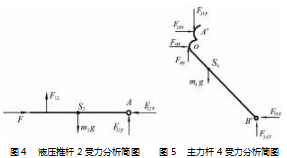
如图 3 所示, 已知推靠液压推杆初始位置为 A, 以 V1 匀速轴向向下运动, 且杆件 OA 与 OB 的夹角为恒定角 θ3.取两铰链固定点为 X 轴, Y 轴过 O 点, 设 AA′、AO、 OA′、OB′对应 杆件长度分别 为 lk 、l3 、l3′、l4′, 且 AO、OB 、A′O 、OB′分别对应的方位角 θ ( 以 X 轴的正向逆时针度量) 为 θOA′、0 、θOA′、2π-θ1. 对应的矢量为 l3 、l4 、l3′、l
2.1.1 推靠机构工作过程中各构件位置分析
当推靠液压推杆向下运动距离 k 后, 设运动矢量为→lk 。以封闭矢量三角形 AOA′分析杆件 3 (推靠臂) 的转角→ → → →θ1 与 l3′。封闭图形 AOA ′是由矢量 l3 、l3′、lk 所构成。在 矢量三角形中, 矢量相加和为 0. 故建立封闭矢量方程 如下:
→ →l3 + l= lk (1)
以复数形式表示为:
l3 ei·θOA + l3′·ei·θOA′ = lk ei·θ (2)
式中:θOA = π+ θ3.θOA′= θ3 -θ1.l3′、θ1 为未知量。
按欧拉公式展开得:
l3 [ cos ( π+ θ3)+ i · sin ( π+ θ3) ] =
l3′[ cos ( θ3 -θ1)+ i · sin ( θ3 -θ1) ]+ lk
化简, 且令等式两边实部虚部相等可解得:
2 lk l3 ( cos θ3 -1 )
可知, 推靠杆 A 点空间位置为:
按封闭矢量图形 A′OB′A′分析构件 4 (推靠臂) B 点 位置。矢量三角形 A′OB′是由矢量 l3 、l4′、lA′B′所构成,
建立封闭矢量方程如下:→—— —→
l3 + l4′= lA′B′
以复数形式表示为:
l3′·ei·θOA′+ l4′·ei ( 2π-θ1) = lA′B′·ei ( 2π-θ1+θ2) 式中:θ2 和 lA′B′为未知量。
按欧拉公式展开, 令等式两边实部虚部相等得:
{-l3′sin θ3 -l4′sin θ1 = -lA′B′· sin ( θ1 -θ2) (8) 等式两边同时平方, 解得:
lA′B′= ^ (9)
可知, B 点的空间位置坐标为:
y(x)A(A)
由构件 5 (推靠板) 位于构件 4 (推靠臂) 与构件 6
(辅助臂) 中心线上, 故构件 5 的平面位置坐标为:
-+yA(x)A + l5/2 (11)
2.1.2 推靠机构工作过程中各构件速度分析
在 A 点进行对杆件 3 进行速度分析, 设 A 点的合运 动 vA , 那么vA = v1/cos θ1 (12)
故ω3 = v1 cos θ1/l3 (13)
杆件 3 与杆件 4 固定连接, 以 O 点为铰链中心做圆周运动, 即·cos θ1 (14)将四边形 OB′CD 看 成封闭的矢量多边形分析, 以→ → → →l4′、l5 、l6 、lOD 分别表示各构件矢量[8], 该机构的封闭矢 量方程为:
→ → → →
l4′+ l5 = l6 + lOD (15)
以复数形式表示为:
l4′·ei ·( -θ1) + l5 = l6 ei ·( -θ1) + lOD(→) (16)
将式 (6) 对时间求导数得:
l4′·ω4′i ei ·( -θ1) + v5 = l6 ω6 i ei ·( -θ1) (17)
上式为 vB +vCB =vc 的复数矢量表达式。将式的实部 与虚部分离, 有
{l4′
联解上式可求得两个速度 v5 、ω6. 即
{ ω6 =
且 v5 为过连杆质心作与原点 O 连线的垂线上。
2.1.3 推靠机构工作过程中各构件加速度分析
将式 (16) 对时间 t 求导, 可得
i ·l4′ω4′2 ei·(-θ1) + l4′ε4′ei·(-θ1) + ε5 =i ·l6 ω62 ei·(-θ1) + l6 ε6 ei·(-θ1) (20)
式 (20) 为 εB +εC(t)B +εC(n)B = εC(t) +εC(n) 的复数矢量表达式。
将式 (20) 的实部与虚部分离, 有{ l4′ω4′2 cos θ1 -l4′ε4′sin θ1 = l6 ε6sin θ1+ l6 ω62 cos θ1(21)
联解上式可求得加速度 ε5、ε6. 即
{ ε6 = (22)
设推靠板质心 EE 在连杆 5 上的位置矢量为a(→), 质心
→
在坐标系 xoy 中的绝对位置坐标为 lE = l4′+ a(→), 则 → →
lE = l4′+ a即lE = l4′ei·(-θ1)
将式 (24) 对时间 t 分别求一次和二次导数, 并经变换整理可得 v 和 εE 的矢量表达式[9] 。
vE = i l4′ω4′( cos θ1 - sin θ1)+ v5/2
εE = il4 ′ω4 ′2sinθ1+ l4 ′ω4 ′2cosθ1+ (l4′ε4′cos θ1-
l4′ε4′sinn θ1) + α5/2 (25)
2.2 推靠机构工作过程动力学分析
动力学分析符号说明: F 为液压缸给液压推杆的作 用力; T 为井壁对推靠板的作用力; mi 、Ji 分别为构件 i 的质量和对其质心的转动惯量; Fijx 、Fijy分别为通过回转 副第 i 个 构 件 给 第 j 个 构 件 在 x 、y 方 向的 约 束 反 力; (LIJ ) x 、 (LIJ ) y 分别为由点 I 到点 J 的矢量在 x 、y 方 向的分量; aSix 、aSiy为第 i 个构件的质心 Si 的加速度在 x、 y 方向的分量;εi 第 i 个构件的角加速度; g 为重力加速 度 [ 10] 。运动学求解部分已经得到了各杆件的加速度, 从 而可求出各杆件所受的惯性力以及惯性力矩。根据支臂 受力情况, 分别以各构件为研究对象, 建立动力学平衡 方程。
(1) 液压推杆 2 受力情况如图 4 所示。动力学平衡 方程为:
F 图 4 液压推杆 2 受力分析简图 图 5 主力杆 4 受力分析简图
(2) 主力杆 4 受力情况如图 5 所示。动力学平衡方 程为:
F24x + Fox -F54x = m4 aS4x -F24y + Foy -m4 g + F54y = m4 aS4y -F24x ( LS4A′) y -Fox ( LS4O ) y + F54x ( LS4B′) y + F24y ( LS4A′) x -Foy ( LS4O ) x + F54y ( LS4B′) x = J4 ε4(27)
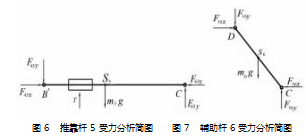
(3) 推靠杆 5 受力情况如图 6 所示。动力学平衡方 程为:
{F-图 6 推靠杆 5 受力分析简图 图 7 辅助杆 6 受力分析简图
(4) 辅助杆 6 受力情况如图 7 所示。动力学平衡方
程为:
F16x -F56x = m6 aS6x
F16y ( LS6D ) x + F56y ( LS6C ) x = J4 ε4
3 MATLAB 建模
生成了 用 于 推 靠 机 构 位 置 分 析 的 MATLAB 代 码。
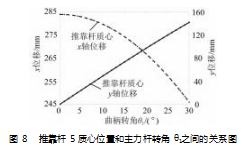
MATLAB 编程的目的是计算推靠机构给定最大推靠位置 时主力杆与井下原位测量装置轴线夹角 θ1 的值。推靠机 构分析的输入变量包括: 推靠机构各杆件长度[ 11 -12]; 主力杆角速度 ω1 。 图 8 显示了各种系统配置中推靠杆 5 质心位置和主力杆转角 θ1 之间的关系, 当 θ1 =29.3°时,推靠机构推靠杆推靠最大行程达到 257 mm。
图 8 推靠杆 5 质心位置和主力杆转角 θ1
4 ADAMS 运动学仿真分析与结果ADAMS
运动学仿真的目的有:
(1) 通过脚本控制的各模块运动,在作业过程中产生运动干涉;
(2) 通过分析 ADAMS 软件后处理的仿真结果来判 断原有 模 型 设 计 仿 真 是 否 能 够 满 足 设 计 要 求 与 技 术 指标[13] 。
在 Solidworks 中建立井下原位测量装置的三维简化模型, 并只保留井下原位测量装置推靠机构, 将建立的三维模型另存为 Parasolid ( *.x_t ) 格式输出, 然后导入 Adams 环境中如图 9 所示, 工作过程中, 推靠机构 2 个极板的运动状态是相同的, 所以通过简化模型, 运用 Adams 中的 Adams/view 模块只对该推靠机构中的一组机 构进行结构参数化设计[14], 并在各关键点处添加约束如 表 1 所示设置推靠机构的运动参数, 为 1 d 在运动副的 Function ( time ) 栏设置曲柄 l1 旋转位移为 1d *time 。
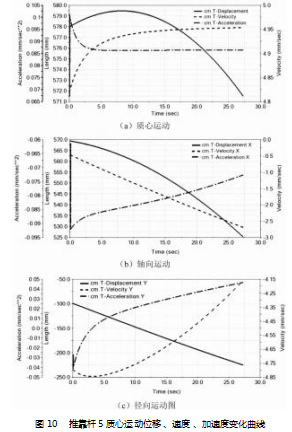
在 ADAMS/View 中创建完推靠机构后, 下一步就是对该模型进行仿真, 并得到输出结果。 推靠臂与井下原位测量装置轴线最大夹角为 29.3°, 主力杆 4 不能完全 360 度旋转, 只能振荡, 所以在 ADAMS 中以 0-29.3 s 为间隔, 仿真步数设置为 1 500 进行仿真, 并通过后处理 Postprocessor 功能 对 虚 拟 样 机 仿 真 运 动 结 果 进 行 分 析 分析[15] 。
由图 10 ( a ) 可知主力杆 4 在液压推杆 2 的作用下, 由静止状态开始受力, 推靠杆 5 加速度有突变, 此情况 下可能会引起整个仪器的振动。推靠杆质心的线速度也 会在一段时间内变化然后变成常数[16] 。 图 10 ( b) 表明 推靠杆 5 质心位置沿着 x 轴方向移动 42 mm, 图 10 ( c ) 表明推靠杆 5 质心位置沿着 y 轴方向移动 120 mm, 最大 测 量 井 径 达 到 260 mm。将 ADAMS 仿 真 结 果 与 前 面 matlab 理论仿真结果 ( 图 8) 对比分析, 可发现理论仿 真的结果基本符合 ADAMS 仿真结果, 能够正确反映出 实际的运动轨迹与趋势, 满足设计要求。
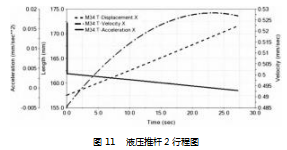
由图 11 可知, 液压推杆 2 运行初期由于各铰接点间存在一定的间隙出现加速度突变, 在推靠杆达到最大推靠位置时, 沿 x 轴方向平移了 34.5 mm, 由此液压推杆行程得以确定。
5 结束语
(1) 基于复数矢量法构造推靠系统运动机构参数方程, 建立了井下原位测量装置推靠机构模型, 为井下原 位测量装置推靠机构系统的理论研究和生产制造提供了 依据。
(2) 通过对推靠系统数学模型的运动分析, 研究推 靠系统中液压推杆的运动行程以及机构中输出构件推靠 杆的运动曲线, 得到其推靠系统各杆件运动参数, 真实反映推靠系统的实际运动状况。
(3) 通过推靠系统运动学分析获取的运动学参数, 为其结构参数优化设计提供参数支撑, 以便进一步优化 井下原位测量装置, 提高设计效率。为后续的动力学分 析以及推靠杆的摩擦 、磨损分析也奠定了基础。
参考文献:
[1]鲍忠利,于会媛,侯洪为.常见测井仪器推靠器结构综述[ J]. 石油矿场机械,2010.39(05):84-88.
[2]任涛,张飞,张春琳,等.新型分动式六臂井径测井仪推靠系统运 动学及动力学分析[J].机械传动,2019.43(06):117-124.
[3]宋红,张魁峰,张春琳,等.微电阻率扫描测井仪极板推靠机 构研究[ J]. 西 安 石 油 大 学 学 报 ( 自 然 科 学 版),2021.36 (06):103-109 +116.
[4]陈俊.地层信息原位测量装置设计及运动特性研究[ D].西 安石油大学,2021.10 ~ 12
[5]宋少云,尹芳.ADAMS 在机械设计中的应用[ M].北京:国防 工业出版社,2015:45-49
[6]魏学良,李俊杰,曹卫东,等.过套管地层电阻率测井仪的研 发设计[J].电子设计工程,2017.25(09):87-91.
[7]侯志利,李瑞琴,武文革.混合驱动五杆机构的运动学解析法 对比研究[J].机械传动,2015.39(11):13-17.
[8] 赵斌.基于 MATLAB 的 VSP 测井仪推靠机构的优化设计 [J].石油矿场机械,2008(06):42-45.
[9] 白金婷,潘存云,吴懋亮,等.基于 TRIZ 的零售柜自动货门设 计及运动学分析[J].机电工程,2020.37(07):836-840.
[10]张策,等.机械动力学[ M]:2 版. 北京:高等教育出版社,2008 33-36.
[11] 曲 秀 全,焦 映 厚, 陈 照 波. RPR -RPP 六 杆 Ⅱ 级 机 构 的MATLAB 运动学仿真[J].机械传动,2003(05):18-21.
[12]胡宇航,张尚盈,张晓艳.基于 MATLAB 的 6R 机械臂运动学的仿真研究[J].制造技术与机床,2022(11):27-32.
[13]任涛,冯斌,孙文,等.测井仪推靠系统机构动力特性分析与 研究[J].西南石油大学学报( 自 然科学版),2019.41(05) : 169-180.
[14]徐芳,周志刚.基于 ADAMS 的凸轮机构设计及运动仿真分 析[J].机械设计与制造,2007(09):78-80.
[15]唐琼.基于 ADAMS 的凸轮机构分析与动态仿真[J].安徽理 工大学学报( 自科版),2010.30(4):22-24.
[16]Yu Hong G,Cheng-Nan S,Engineering S O.Roller Translating Follower Disc Cam Design and Simulation Based on ADAMS [J].EducationTeachingForum,2019.21(12):69 ~74.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/56859.html