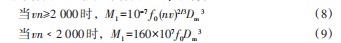SCI论文(www.lunwensci.com):
摘要:影响高精度机床加工误差的主要为热误差,约占机床总误差的40%~70%,其中电主轴的热变形是最为直接的因素。介绍了KX-1电主轴结构特点,计算了电主轴的热载荷、热边界条件,采用软件Workbench建立了电主轴有限元模型,进行了电主轴热-结构耦合分析。仿真结果表明,无冷却系统的电主轴最高温度达256.53℃,位于定子与转子相邻部位;设置冷却系统后电主轴最高温度为60.448℃,位于前轴承处。对设置冷却系统的电主轴进行稳态热分析,沿轴向(X向)最大变形值为23.179μm,位于前端;轴芯总的热变形为22.636μm,精密加工时须进行热误差补偿。
关键词:电主轴;热生成;热变形;有限元分析
Thermal Characteristic Simulation Analysis of KX-1 Motorized Spindle Based on ANSYS
Chen Yuming1,Chen Pengman1,Wang Zhu2,Yang Chuangang1,Wang Tianlei2
(1.Jiangmen Kelson Industry Ltd.,Jiangmen,Guangdong 529000,China;2.Faculty of Intelligent Manufacturing,Wuyi University,Jiangmen,Guangdong 529020,China)
Abstract:The main factor affecting the machining error of high-precision machine tools is thermal error,which accounts for about 40%~70%of the total error of machine tools.The thermal deformation of motorized spindle is the most direct factor.The structural characteristics of KX-1 motorized spindle was introduced,the thermal load and thermal boundary conditions of the motorized spindle was calculated,the finite element model of the motorized spindle by using the software workbench was established,and the thermal structural coupling analysis of the motorized spindle was carried out.The simulation results show that the maximum temperature of motorized spindle without cooling system is 256.53℃,which is located near the stator and rotor.After setting the cooling system,the maximum temperature of the motorized spindle is 60.448℃,which is located at the front bearing.Conduct steady-state thermal analysis for the motorized spindle with cooling system,and the maximum deformation value along the axial direction(X direction)is 23.179μm,at the front end.The total thermal deformation of the shaft core is 22.636μm.Thermal error compensation must be carried out during precision machining.
Key words:motorized spindle;thermal generation;thermal deformation;finite element analysis
0引言
高速电主轴具有高转速、宽调速、低噪声、易于控制等特点,是机床的关键功能部件,其速度、功率、扭矩、动态刚度和热特性与加工精度有密切关系,是机床中最大的热源[1-2]。高速运转的电主轴不可避免的产生大量热量,其各个部件会产生不同程度的热膨胀,导致机床加工精度和可靠性下降。研究表明:影响高精度机床加工误差的主要因素是热误差,约占机床总误差的40%~70%[3-4]。因此,要求电主轴需具备良好的热-结构性能。在电主轴热特性方面,国内外学者做了许多研究[5-10],分别对配套高速数控车削中心、铣削中心的不同型号、不同结构的电主轴进行了结构-热特性分析与研究,可为进一步提高电主轴的精度提供参考。
本文以KX-1电主轴为研究对象,计算了该电主轴内置电机的损耗生热、轴承摩擦生热、热载荷,以及热边界条件,采用软件Workbench建立了电主轴有限元模型,进行了电主轴热-结构耦合仿真分析,研究其热变形规律,为提高数控机床的加工精度和机床精密加工时进行热误差补偿提供参考。
1高速电主轴结构
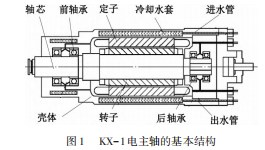
KX-1电主轴的基本结构如图1所示。
(1)高速电主轴电机。电主轴电机采用变频调速,额定电压380 V;工频50 Hz;额定转矩14 N⋅m;额定功率2.2 kW;极对数2;最高转速24 000 r/min。
(2)高速电主轴轴承。电主轴前后均采用角接触混合陶瓷球轴承(参数见表1),背靠背的配列可承受两个方向的轴向载荷和较高的倾覆力矩。
(3)轴承润滑系统。轴承润滑系统可减少摩擦和磨损,带走轴承的部分热量。润滑方式有油润滑和脂润滑,一般根据速度参数Dmn(Dm为轴承中径,n为转速)来确定。当Dmn<1.0×106时,采用脂润滑;当Dmn≥1.0×106时,采用油润滑。KX-1高速电主轴速度参数Dmn>1.0×106,采用油气润滑,可控制最佳油量,冷却效果好,温升低,尘埃和切削液不易侵入,几乎无环境污染等特点。
(4)冷却系统。图2所示为电主轴的温升主要来源为内部的电机和轴承。图3所示为电主轴热传递路径,轴承可通过油气润滑带走一定的热量;电机产生的热量主要通过定子外水套中的循环冷却水带走。
2高速电主轴的热
2.1发热计算
2.1.1电机发热量
电机的发热是由于各种损耗最终转化而成,主要损耗有机械损耗、磁损耗、电损耗和附加损耗,其中附加损耗在总损耗占比很小,通常忽略。
(1)机械损耗
机械损耗是电机转子在运转时与空气的摩擦,产生的摩擦损耗,主要位置在转子外围与定子的间隙处,计算公式为:
式中:Pn为机械损耗功率,W;C为空气摩擦系数(通常以经验来确定);ρ为空气密度,kg/m3;ω为角速度,rad/s;R为转子外半径,m;L为转子长度,m。
(2)磁损耗
磁损耗包括磁滞损耗和涡流损耗,是主磁场在铁心内发生变化时产生,不论是交变磁化还是旋转磁化,在铁心中都会引起磁滞损耗和涡流损耗。单位质量铁磁物质内由交变磁化引起的磁滞损耗可用下面的公式计算:
式中:Pt为磁损耗功率,W;C为取决于材料性能常数,C=1.6~2.2;f为磁化频率,s-1;Bm为磁通密度最大幅值,通常(1.0 T≤B≤1.6 T),T为磁感应强度。
单位质量内的涡流损耗功率Pe计算公式为:

式中:为涡流损耗功率,W;t为硅钢片厚度,mm;rc为铁心密度,kg/m3;ρ为铁心电阻率,Ω·m。
磁损耗功率公式为:

(3)电损耗
电损耗就是电机内定子和转子线圈自身内阻的损耗,计算公式为:

式中:Pc为电损耗功率,W;I为电流,A;R为导体的电阻,Ω;ρ为导体的电阻率;L为导体的长度,m;S为导体的截面积,m2。
电机总损耗功率为:
2.1.2轴承发热量
轴承高速运转时存在滚动摩擦、滑动摩擦和粘性摩擦,其中粘性摩擦是当润滑油逐渐累积后,在轴承滚珠和润滑油之间形成的,该摩擦也会产生一定的热量。
(1)轴承摩擦力矩
轴承摩擦力矩有滚动摩擦力矩和粘性摩擦力矩,由palmgren公式可求得轴承摩擦力矩M:
M=M1+M2(7)
式中:M1为粘性摩擦产生的摩擦力矩,M2为轴承承受载荷产生的摩擦力矩。粘性摩擦力矩M1的计算:
式中:v为润滑剂运动粘度;f0为与轴承类型和润滑方式的系数;Dm为轴承的节圆直径。
载荷摩擦力矩公式为:
式中:P为轴承载荷;f1为与轴承结构、载荷有关的系数。
所以轴承摩擦力矩:
(2)轴承摩擦发热量
轴承滚动体和滚道接触区的摩擦发热量为:
式中:Q为轴承摩擦发热量,W;M为总摩擦力矩,N·mm;n为轴承转速,r/min。
2.2传热分析
定子外水套中的循环冷却水可带走电主轴大部分热量,其他热传递方式[11-12]分析如下。
(1)轴承与油气润滑的对流换热
轴承采用油气润滑,即通过喷嘴将油气混合物喷向轴承,起降温作用的是压缩空气的对流换热,因此,首先要知道空气流过轴承的流动面积:
式中:Aax为轴向空气流过轴承的面积,m2;dm为轴承平均直径,m;Δh为轴承内外套与保持架之间的间隙,m。
轴承中空气的流动速度可以通过下式得到:
式中:μ为轴承中空气平均速度,m/s;ν1为轴承中实际空气的流量,m3/s;ω为主轴旋转角速度,rad/s。
轴承与压缩空气的对流传热系数为:
式中:α为轴承与空气的换热系数,W/(m2·k);c0、c1、c2可通过试验测得,通常分别取9.7、5.33、0.8。
(2)电机定子与冷却系统对流换热
循环水流通过定子外部水套带走电主轴内部大部分热量。传热系数与水流速、流道截面积和流体流动状态有关,需先判断水的流态,雷诺数Re计算公式为:

式中:u为流体的特征速度,m/s;D为几何特征定性尺寸,m;v为冷却水的运动粘度,m2/s。
通常将水流状态分为层流、过渡态和湍流。
当Re≤2 200,水流状态为层流,其公式为:
Nu=1.86(RePrf L/D)1/3 (17)
当2 200≤Re<10 000时水流状态为过渡态。
当Re>10 000时为湍流状态,其公式为:
Nu=0.023 Re0.8Pr0.4 (18)
式中:Nu为努塞尔数;Pr为普朗多准数。
冷却水强迫对流换热系数,其公式为:
α=(Nu·λ)/D (19)
式中:a为冷却水的对流换热系数,W/(m2·K);λ为水的导热系数,W/(m·k);D为管道定性尺寸,m。
(3)电机转子换热
与定子散热方式不同,转子是通过自身旋转带动空气对流换热和辐射换热,需计算空气对流换热和辐射换热,计算式为:

式中:α为转子端部的换热系数,W/(m2·K);u为转子端部的周向速度,m/s;n为电主轴的转速,r/min;d为转子端部的平均直径,m。
(4)电主轴和周围空气的换热
电主轴运行时产生温升,并向环境传递热量,属自然对流换热,换热系数为:
a=9.7 W/(m2·K)
3电主轴热态特性有限元分析
3.1 ANSYS热分析基本步骤
ANSYS仿真分析基本步骤是构建模型、网格划分,施加载荷、求解与后处理。
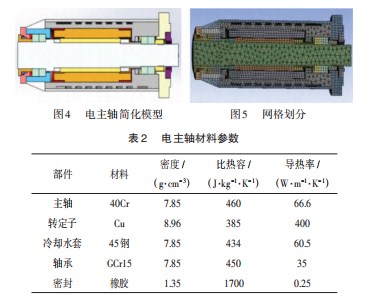
(1)构建模型。图4所示为在不影响热分析前提下,简化的电主轴Solidworks模型。材料属性设置如表2所示。
(2)网格划分。采用网格自动划分,网格数33 479个,节点数105 970,网格划分如图5所示。
(3)施加载荷。热载荷为电机转子和定子生热率与前、后轴承的生热率。
(4)求解和后处理。将载荷和边界条件加入后可进行求解,求解量为temperature,可得温度分布图,如图6所示。
3.2热载荷的计算
KX-1高速电主轴为定子外套循环水冷结构、功率为2.2 kW,工作转速为18 000 r/min时,依照计算式(1)~(12)可得电机和轴承发热量。
(1)电机生热率。计算得到定子发热量Q=0.293 kW,转子发热量为0.146 7 kW。
生热率计算公式为:
q=Q/V(22)式中:Q为热源的发热量,W;V为热源体积,m3。
计算可得电机定子、转子的生热率分别1.698×106 W/m3,3.706×106 W/m3。
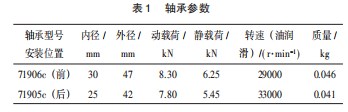
(2)轴承生热率。由表2中对角接触陶瓷球轴承的参数,计算可得前、后轴承的发热量分别为102.1 W、73.1 W,进而可得前、后轴承生热率分别为11.041×106 W/m3、9.089 7×106 W/m3。3.3边界条件的确定电主轴的边界条件如下,对流换热系数:(1)电机转子端部换热系数为132.916 W/(m2·K);(2)润滑系统与轴承处对流换热系数,前轴承为104.11 W/(m2·K),后轴承处为94.335 W/(m2·K);(3)电主轴表面与外界空气自然对流的换热系数为9.7 W/(m2·K)。设置工作环境温度为24℃。
3.4稳态热分析
电主轴工作时产生温升,与外部介质进行对流、导热和热辐射而冷却,最终达一稳定温度[13],即热平衡或热稳态。稳态热分析的主要目的是计算并确定由稳定的热载荷所引起的温度变化、热梯度分布、热变形等情况[14]。
在完成热载荷和边界条件设置后,可将其加载到模型中进行热稳态分析。
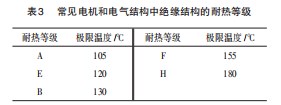
(1)无冷却系统的电主轴温度分布如图6(a)所示,最高温度达256.53℃,集中在定子与转子相邻部位。最低温度为227.2℃,远超过表3所列电机和电气结构中的耐热等级H,必须设置冷却系统。
(2)图6(b)为设置冷却系统后电主轴温度场,稳定运转后最高温为60.448℃,位于前轴承处。最低温为26.927℃,位于冷却流道入口,其他位置温度分布较均匀,冷却系统抑制电主轴温升效果明显。
3.5电主轴热-结构耦合的热变形
3.5.1电主轴热变形
将电主轴的稳态热分析后的数据导入静力学分析模块,可得图7所示电主轴热稳态时总变形。从图中可看出最大变形的位置出现在主轴前端,形变值为23.179μm,无法满足高精数控机床要求,需采取措施抑制温升,或进行温度误差补偿。
3.5.2轴芯热-结构耦合分析
前面分析表明,电主轴各部分均有程度不同热变形,轴芯与刀具相连,其热变形将直接影响机床加工精度,下面对轴芯热-结构耦合进行分析。
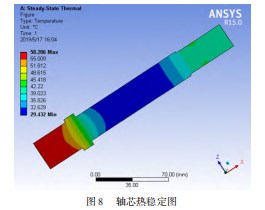
(1)轴芯稳态温度场分析。轴芯是整个电主轴重要组成部分,承接了转子与前、后轴承中较大部分热量,图8所示为轴芯热稳态图,其前端最高温度达61.614℃,热量来自前轴承摩擦生热和转子电磁损耗生热,是热量集中区域。
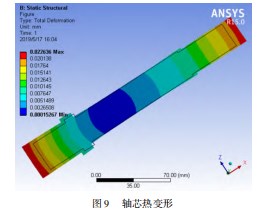
(2)轴芯的热变形。将稳态热数据导入静力学分析中,可得轴芯总热变形图9,轴芯总变形为22.636μm,分别沿轴向(X方向)两端延伸,该方向热伸长直接影响加工精度,可通过热误差补偿解决。
3.6不同转速时电机温度场分析
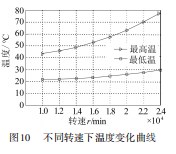
高速电主轴结构复杂,影响电主轴温度的因素较多,本文仅分析不同转速对前、后轴承,以及电主轴整体温度场变化的影响。图10所示为其他因素不变,仅改变转速进行仿真实验结果,电主轴的最高温和最低温均随转速增加而增加,温度和转速呈非线性的正相关关系。图11所示为不同转速电主轴温度场。
4结束语
(1)本文分析了KX-1高速电主轴电机损耗生热和轴承的摩擦生热,电主轴的热载荷、热边界条件的计算,有限元仿真分析表明,无冷却系统时电主轴最高温度达256.53℃,位于定子与转子相邻部位;设置冷却系统后电主轴最高温度为60.448℃,位于前轴承处。
(2)稳态热分析表明,沿主轴轴向(X向),电主轴最大变形值为23.179μm,位于前端;轴芯最大热变形为22.636μm。轴向的热伸长直接影响机床加工精度,精密加工时须进行热误差补偿。
参考文献:
[1]张伯霖,杨庆东,陈长年.高速切削技术及应用[M].北京:机械工业出版社,2002.
[2]何强,李安玲,李丽丽,等.精密电主轴结构设计及测控技术发展现状[J].安阳工学院学报2016,15(2):1-10.
[3]肖曙红,张伯霖,陈焰基,等.高速电主轴关键技术的研究[J].组合机床与自动化加工技术,1999(12):5-10.
[4]陈兆年,陈子辰.机床热态特性学基础[M].北京:机械工业出版社,1989.
[5]邹里云,仇晓黎,赵义顺.CKH1463精密数控车削中心电主轴热特性分析机床与液压[J].2013,41(13):20-25.
[6]黄晓明,张伯霖,肖曙红.高速电主轴热态特性的有限元分析[J].航空制造技术,2003(10):20-23.
[7]刘一波,张晓龙,吴智恒.DGZX-1230型高速电主轴稳态温度场分析[J].机电工程技术,2016,45(2):30-36.
[8]卢立河,赵晶,王世杰.串行轴承组均载性能及承载能力分析[J].机电工程,2021,38(10):1269-1276.
[9]陈鹏满.KX-1主轴电机冷却流道结构设计与仿真分析[J].机电工程技术,2021,50(6):88-92.
[10]Chen J S,Hsu W Y.Characterizations and models for the ther⁃mal growth of a motorized high speed spindle[J].International Journal of Machine Tools&Manufacture,2003(43):163-170.
[11]刘剑,肖民.基于ANSYS的空气静压电主轴热变形研究[J].机电工程技术,2010,39(11):34-37.
[12]黎贤钛.电机运行热交换计算与设计[M].杭州:浙江大学出版社,2016.
[13]T Holkup,H Cao,P Kolar,et al.Thermo-mechanical model of spindles[J].CIRP Annals-Manufacturing Technology,2010,59(1):365-368.
[14]刘道钱,陈涛,沈顺成,等.数控铣床主轴部件动态特性分析[J].机械设计与制造,2008(4):172-174.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/49562.html