SCI论文（www.lunwensci.com）:
摘要：航空发动机脉动式装配过程中涉及的任务数量多，约束数量多且关系复杂，对排产速度要求极高，需要高效的排产算法支持。从工艺过程和生产管理要求出发，深入地分析了排产面临的约束条件与优化目标；在对比多种排产算法的基础之上，提出了多规则融合算法，是对基于规则的普通排产算法的升级。在此算法中装配工艺和有限资源等刚性约束被以算法流程的形式加以贯彻和实施；在不违反刚性约束的前提下，算法循环地利用综合评价的方式对满足约束条件的多个生产任务进行评估，从中选择最佳的任务，优先安排生产，直到所有的任务都被安排。与常规的元启发式算法相比，多规则融合算法对约束的遵守力度更高，扩展更为便利；更重要的是，由于避免了随机扰动、反复叠代和群体计算，其结果具有确定性，求解速度非常高，非常适合工程应用。
关键词：航空发动机；脉动装配线；排产；算法
A Study on the Scheduling Algorithm for Aero-Engine Pulsed Assembling Line
Zhang Bo1，Wang Yuanyuan2，Song Yingjun2，Wei Xiaohong2，Huang Jian2
(1.China Aviation Planning and Design Institute(Group)Co.,Ltd.,Beijing 100120,China;2.Xi'an Aero-Engine(Group)Co.,Ltd.,Xi'an 710021,China)
Abstract:Aero-Engine pulsed assembling process involves many tasks and complex constraints,and has very stringent demand on responsiveness.A high efficient algorithm is in dire need.Starting from assembling process and related management requirements,the scheduling problem's constraints and objectives was analyzed.After comparing multiple scheduling algorithms,a Multi-Rule Fusion(MRF)algorithm was proposed.It was an upgrade to regular rule-based scheduling algorithm.With MRF,rigid constraints such as assembling process and limited resources were implemented through algorithmic process,and multi-criteria decision models were employed to select optimal task iteratively for dispatching till all tasks were scheduled.Compared with regular mete-heuristic schedule algorithm,MRF is much more constraints compliant and extension-friendly.More important than that,due to its evasion of random perturbations,massive iterations and swarm calculations,it is deterministic and much faster,which is very desirable for engineering applications.
Key words:aero-engine;pulsed assembling line;scheduling;algorithm
0引言
脉动式装配是对传统固定站位式装配方式的巨大革新，也是世界主流的发展趋势[1-3]。这种装配方式通过在生产组织、调度安排、物流配送、人员技能等各个方面进行相应地适应和调整来解决传统固定站位式装配过程中面临的种种问题[4]。在脉动式装配过程中，随着站位和节拍的引入，生产过程更加紧凑，个别装配任务的拖期对整个装配流程的影响和冲击很容易得以凸显和放大[5-6]。由于装配过程和供应链管理的复杂性，要完全消除这些拖期几乎是不可能的。面对数十乃至数百道装配工序，各种各样的约束条件，一线生产管理人员很难临时快速做出高质量的排产调度决策。为此，采用科学、高效的排产调度方法，在发生拖期的情况下临时对装配任务进行重新安排，减少对整个装配流程的不利影响。对于脉动式装配，学术界历来关注的重点是站位的平衡问题，即在确定的节拍下力求站位数量最少(第一类平衡问题)，或在确定的站位下力求节拍最短(第二类平衡问题)[7-8]。并且在进行站位平衡时，通常关注的是装配工时在站位之间的协调性，不考虑装配人员工作负荷的饱满性和平衡性。这使得脉动式装配生产线在实际运行过程中往往面临以下困难：(1)装配顺序仍需进一步确定；(2)人员调度仍需进一步解决；(3)无法适应生产过程中出现的各种异常。汪圆[9]、蔡玮[10]等借助元启发式算法对于飞机脉动装配过程中的中小型的人员调度问题进行了求解，取得了较好的效果。然而，发动机装配过程中涉及的任务数量更多，工时更短，对排产的响应速度要求更高，相关研究较少。本文从工艺过程和生产管理要求出发，深入地分析了其排产面临的约束条件与优化目标；在对比多种排产算法的基础之上，提出了多规则融合算法。与常规的元启发式算法相比，多规则融合算法对约束的遵守力度更高，扩展更为便利，其结果具有确定性，求解速度高，适合工程应用。
1约束条件与优化目标
1.1约束条件
发动机脉动装配过程中，多台分别处于不同装配状态的发动机被吊装在轨道吊车上，按照统一的节拍改变站位。完成所有站位的装配工作后，轨道吊车返回到第一站位，接受新的发动机装配任务。排产时面临的约束条件主要包括以下几个方面。
(1)工艺约束。工艺约束即装配过程中必须遵守的先后顺序。装配任务之间的先后顺序通常比较复杂，表现为网络状。除了关键路线上的装配任务，其余任务的执行时段都可以在一定范围内浮动。
(2)站位约束。由于采用了脉动式的装配方式，一些装配过程中所需使用的专用设备被固定设置在特定的站位上。这使得与之相应的装配任务必须在这些特定的站位上才能执行。
(3)资源约束。尽管总装部份出于缩短装配周期的考虑，为各项装配任务配备了专用的资源，大大减少了资源共用的情况，使得从理论上来讲可以消除许多资源约束。但是，为了应对可能的设备故障、人员短缺等各种意外情况，依然有必要把各类资源的数量作为参数纳入排产调度的计算模型中，以便于在需要的时候可以通过简单地修改参数，实现对异常情况的快速响应。
(4)班制约束。发动机装配是劳动力密集的制造环节，因此在排产调度的过程中非常有必要把安全生产和人性化的因素纳入考虑。为此，排产调度结果应当尽可能地与班制时间吻合。例如，在8 h的工作班制下，尽可能地使得装配工作不要跨越上、下午的两个4 h的工作时段，也尽力不要跨越工作日。这是因为跨越工作时段的装配工步，一方面容易对装配工人产生精神压力；另一方面容易造成工作遗漏和安全事故。
(5)空间约束。发动机的装配需要多人共同协作。而为了实现并行工作，缩短装配周期，常常还需要增加装配的人员数量。这可能会导致装配人员因为间距太近而导致相互之间形成动作干涉，影响装配效率。为此有必要在一些装配环节，例如，风扇主体外壳的支架安装，划分相互独立的工作区域。一个工作区域内在一个时刻只能允许一个装配任务。由于大量装配人员并行操作是造成工作区域紧张的主要原因，所以减少并行操作是规避空间约束的有力措施。为了简化算法、提高求解速度，也可以在工艺过程梳理部分将许多人员密集型的并行操作进行强制化的串行处理，从而规避上述空间约束。
1.2优化目标
与其他生产线排产时追求工期最短不同，脉动生产线的工期由生产线的节拍决定，因此在这方面没有优化的空间。在此，管理部门关注的优化目标包括：人员工作量的均衡，以及对于排产需求的快速响应。
发动机装配过程中存在着大量可以并行执行的任务，如果不加优化地直接并行，很有可能各时段对包括人力在内的各类资源的需求极不均衡，从而导致各人员的工作量也因此极不均衡。大体而言，有两种方式来提高人员工作量的均衡度：一种方法是直接建立各人员工作时间的统计量，通过控制方差来实现均衡；另一种方法是尽量减少工作人员的总数，通过力争实现各人员满负荷工作来间接地实现工作量的均衡。显然，第二种方式更加具有积极意义，为此，本文采用第二种方式。
尽管发动机装配的周期可能长达几天，分解到具体装配任务上的时间其实并不长，通常只有几分钟到几十分钟。因此，排产调度的响应时间也必须控制在几分钟之内，最好几十秒以内。实际上，在发动机脉动装配的过程中装配时间的严重偏移(提前或拖延)将会是引发重新排产的重要因素。因此，各个装配任务结束时都有可能引发重新排产。所以，重新排产的时间间隔与各个装配任务的工时长度密切相关。以某型号发动机为例，由于各装配任务的工时长度接近指数分布，如图1所示。可以预见，装配过程中的重新排产要求的时间间隔长度也将符合指数分布。如果从响应速度上要覆盖99%重排事件，需要排产的时间小于μ/100，约32 s。考虑到重新触发排产的过程中可能还需要一些人工的手动操作(例如登录系统、刷新数据、启动排产等)，真正留给排产计算的时间可能只有几秒。
图1某型号发动机各装配任务的时间分布
2优化算法
2.1算法选择与对比
当前主流的排产算法主要包括基于大规模搜索的精确解法[11]和线性规划方法[12]，基于约束理论的传统算法[13-14]，基于迭代进化的各类元启发式算法[15]和基于贪心策略的规则算法[16-17]。另外，还有学者提出了基于多代理竞争的分布式决策算法[18-19]，这种采用的分散决策机制具有较强的创新性，但是实际应用较少。
发动机脉动装配线排产问题涉及的任务数量多，约束条件多且复杂，数学表达的难度大，计算速度要求高，不适宜采用精确解法和元启发式算法。脉动式装配中各项生产资源相对比较均衡，瓶颈效应并不突出，所以也不宜采用基于约束理论的传统算法。为此，对于发动机脉动装配线排产而言，比较适合采用规则算法。特别地，为了适应不同约束条件对排产提出的要求，应采用多规则融合算法。
多规则融合算法是对基于规则的普通排产算法的升级。在多规则融合算法中工艺约束和资源约束被以算法流程的形式加以贯彻和实施，以避免对这些“刚性约束”的突破。例如，通过建立装配任务的筛选机制和资源时钟更新机制，使得只有那些完成了其所有前序工序的任务和在所需时段内未被占用的资源才能纳入排产计算。
在不违反刚性约束的前提下，算法将利用综合评价的方式对满足约束条件的多个生产任务进行评估，从中选择最佳的任务，优先安排生产。具体而言，包括以下几个方面的经验性规则：优先处理等待时间最短的任务；优先处理松弛时间最短的任务；优先处理与剩余可用工作时间最接近的任务；优先处理对资源占用最少的任务。
由于这些经验性的规则常常会分别指向不同的结果，因此，需要通过某种量化的方式来对规则进行综合，即多规则融合。常见的综合算法包括加权求和法、加权求积法等。
需要特别说明的是，对于脉动装配线的排产而言，为了避免任务拖延打乱既定的装配节拍，通常需要在惩罚函数的计算过程中给予松弛时间赋予较高的权重。这可能会导致某些原本等待时间较短的任务让位于那些松弛时间较短的任务，从而增加生产过程中的等待时间。为此，在选择惩罚函数最小的任务后，还应检查能否在可执行的任务中找出在惩罚函数最小的任务开始之前就能完成的其他任务。显然，如果存在这样的任务，将其插入不会对惩罚函数最小任务的执行造成任何不利的影响。
2.2排产流程与算法
2.2.1数据准备
该部分的主要任务是获取排产所需的装配节拍、工艺数据、站位数据、班制数据。工艺数据主要包括：各装配任务的编号、工时、用人数量、紧前任务编号、紧后任务编号、所属站位、最早开始时间、最晚结束时间等信息；站位数据主要包括：各站位的编号、人员编号；班制数据主要包括：开工时间、休工时间。
特别需要说明的是，与一般装配过程不同，采用脉动式装配后，由于各站位上并行安装的发动机相互独立，而且这些发动机只有在完成其当前站位上所有装配任务以后才能进入到其下一个站位，所以各站位上装配任务的紧前、紧后任务都只限于是同属于该站位的其他任务。在利用装配任务网络计算各个任务的最早开始时间和最晚结束时间时，必须使用同站位的紧前任务和紧后任务。
为了确保排产计算顺利正确地执行，有必要在此部分对获取的数据进行多角度的合理性检查，并在必要时给出相应的提示或警告。
2.2.2计划排产
该部分负责安排各装配任务的开始时间，并指定相关的操作人员。本文采用多规则融合算法，具体实现过程如下：
(1)读取待排产的任务列表tasksToSchedule，并初始化已排产任务列表tasksScheduled；
(2)筛选出可以执行的装配任务tasksValid，筛选的标准主要是检查紧前任务是否已经被纳入已排产列表tasksScheduled；
(3)确定各可执行任务的最早开始时间、松弛时间等信息；
(4)根据上述信息对各可执行任务进行评价，计算其惩罚函数值；
(5)找出惩罚函数最小的任务，将其确定为最佳任务taskBest；
(6)如果存在完成时间早于上述最佳任务的其他任务taskOther，将该任务确定为新的最佳任务taskBest；
(7)将最佳任务taskBest纳入已排产任务列表tasksScheduled，并将其从待排产任务列表tasksToScehd⁃ule中移除；
(8)更新最佳任务taskBest和相关人员的状态和完成/就绪时间；
(9)返回第(2)步，直到待排产的任务列表tasks⁃ToScehdule被清空。
排产算法流程如图2所示。
3案例分析
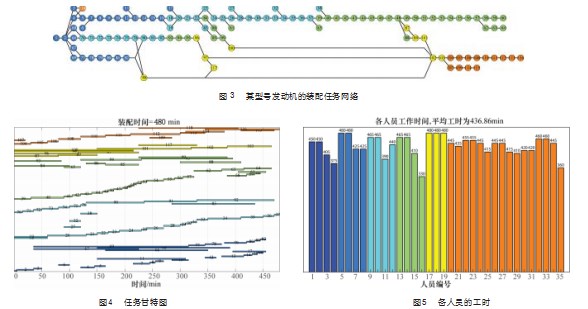
以某型号发动机为例对上述算法进行验证。该型号发动机的装配被划分为118个任务，并被安排到5个站位，脉动周期设计为8 h，其装配任务网络如图3所示。其中，不同站位的任务用不同的节点颜色加以区分。
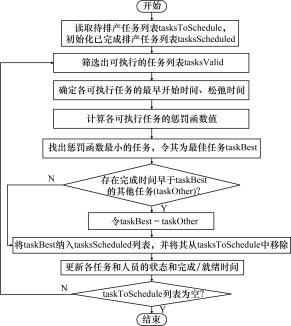图2 排产算法流程
为充分利用人力资源，需要部分人员承担跨站位的装配任务。为此，将人员分为6组，其中5组分别是各站位的常备人员，他们只负责本站位的装配任务；剩下的1组(应急中心)，负责在需要时临时支持各站位。预计投入的装配人员总数为35人，其中1~4站位常备4人，第5站位常备3人，应急中心配备16人。
根据上述约束，利用排产算法进行了求解。如图4所示，各站位的装配时间都不大于8 h，其中最大者为480 min，最小者为455 min。各站位的装配时间比较均衡。如图5所示，各人员的工时分布也较为均衡，平均工时为436.86 min，约占总工作时间的91%。
4结束语
航空发动机脉动装配线排产以提高人员劳动生产率为目标，它具有问题规模大，约束条件多且复杂，响应速度要求高等特点。规则算法和元启发式算法是求解工程实际排产问题的两大主流方法。然而，面对动态调度对求解速度提出的苛刻要求，依赖反复叠代和群体计算的元启发式算法无法胜任。此外，元启发式算法在转化生产规则方面的手段较为单一，对于复杂规则过度依赖于功效函数，虽然大多数情况下也能找到符合要求的结果，但是其代价却是更为复杂的功效函数或更大的搜索范围——而此举又会进一步加剧求解速度的不足。
本文提出的多规则融合算法是对基于规则的普通排产算法的升级。在多规则融合算法中刚性约束被以算法流程的形式加以贯彻和实施；在不违反刚性约束的前提下，算法利用综合评价的方式对满足约束条件的多个生产任务进行评估，从中选择最佳的任务，优先安排生产。与元启发式算法相比，多规则融合算法对约束的遵守力度更高，扩展更为便利；更重要的是，由于避免了随机扰动，反复叠代和群体计算，多规则融合算法具有确定性，其求解速度非常高，特别适合应用于航空发动机脉动装配线。
参考文献：
[1]孙贵青,赵哲,王彤.涡扇发动机装配脉动装配生产线分析[J].现代制造技术与装备,2018(2):107-109.
[2]李金龙,杜宝瑞,王碧玲,等.脉动装配生产线的应用与发展[J].航空制造技术,2013(17):58-60.
[3]罗鑫,阮亮.脉动式生产线在飞机总装中的应用探索[J].现代制造技术与装备,2019(7):150-152.
[4]魏小红,谈军,方红文,等.航空发动机水平脉动总装生产线规划研究[J].航空制造技术,2015(19):8-12.
[5]Tian Hua Jiang,Hao Xiang Wang.Study on the Self-Evolution Problem of an Aircraft-Engine Assembly Workshop with Uncer⁃tain Number of Assembly Times[C]//Proceedings of the Institu⁃tion of Mechanical Engineers,Part B Journal of Engineering Manufacture,2014.
[6]辛彦秋,吴斌,苏丹,等.民用航空发动机脉动装配浅析[J].航空制造技术,2013(20):118-120.
[7]潘志豪.飞机总装脉动生产线平衡问题研究与应用[D].南京:南京航空航天大学,2018.
[8]郭亚宁,张振明,田锡天,等.脉动模式下基于蚁群算法的飞机装配工序分配方法[J].机械制造,2011(5):49-52.
[9]汪圆.飞机脉动装配线平衡方法与人员调度[D].南京:南京理工大学,2016.
[10]蔡玮.双线并行飞机总装脉动式装配线平衡与调度问题研究[D].成都:西南交通大学,2021.
[11]Michael L Pinedo.Scheduling:Theory,Algorithms,and Systems[M].Switzerland:Springer International Publishing,2016.
[12]H Paul Williams.Model Building in Mathematical Programming[M].Chickester England:John Wiley&Sons,Lid.,Publication,2013.
[13]Mark J Woeppel.Manufacturer's Guide to Implementing the Thoery of Constraints[M].Boca Raton,Florida,USA:CRC Press,2000.
[14]侯伟.基于约束理论的订单排产研究[D].武汉:武汉科技大学,2009.
[15]Yuri Mauergauz.Advanced Planning and Scheduling in Manu⁃facturing and Supply Chains[M].Moscow Russia:Springer,2016.
[16]S S Panwalkar,Wafik Iskander.A Survey of Scheduling Rules[J].Operations Research,1977,25(1-2):45-61.
[18]Jacek Blazewicz,Klaus H Ecker,Erwin Pesch,et al.Scheduling Computer and Manufacturing Processes[M].Berlin,Germany:Springer-Verlag Berlin Heidelberg GmbH.
[19]王玉,罗焕佐,牟洪健,等.基于Multi-agent的优化排产系统的分析与设计[J].计算机工程,2004(12):150-152.
[20]Weiming Shen,Qi Hao.Agent-based Dynamic Scheduling for Distributed Manufacturing[C]//Process Planning and Schedul⁃ing for Distributed Manufacturing,2007.
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/46971.html
