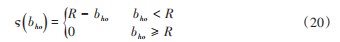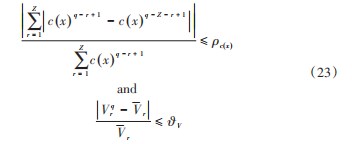SCI论文(www.lunwensci.com):
摘要:拓扑优化是实现传统结构创新式构型设计的常用技术。在此领域内, 变密度法已经成为目前结构优化设计的主流算法。这 种算法基于经典介质理论, 不包括材料尺度参数, 无法捕捉微观结构的信息。为此, 应用双向进化结构优化法取代变密度法, 并 结合偶应力理论而不是经典理论构建了优化列式来进行拓扑优化设计, 最终将两种优化算法得到的结果作对比, 以呈现出不同尺 度下结构的不同构型。结果表明, 在以结构刚度最大化为目标的设计中, 偶应力介质的结果取决于尺度参数的大小, 最优结果具 有明显的尺度效应。通过几个数值算例证明了这种方法适用于具有与单元尺寸相当的固体材料的结构单元设计, 并且拓展了针对 微型结构设计问题的技术手段。
关键词:拓扑优化; 偶应力; 尺度效应; BESO
Bi-directional Evolutionary Structural Optimization Based on Couple Stress Theory
Qiao Heting, Gao Qun, Xiong Zhan
(School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China)
Abstract: Topology optimization is a common technology to realize the innovative configuration design of traditional structures . In this field,olid isotopic material with penalization(SIMP) has become the mainstream algorithm of structural optimization design. This algorithm is based on classical medium theory and does not include material scale parameters, so it can not capture the information of microstructure. Therefore,bi-directional evolutionary structural optimization(BESO) was used to replace SIMP method, and combined with couple stress theory rather than classical theory, an optimization formula was constructed for topology optimization design. Finally, the results of the two optimization algorithms were compared to show different configurations of structures at different scales . The results show that in the design aimed at maximizing the structural stiffness, the result of couple stress medium depends on the size of scale parameters, and the optimal result has obvious scale effect. Several numerical examples show that the method is suitable for structural element design with solid materials equivalent to the element size, and expands the technical means for micro structure design.
Key words: topology optimization; couple-stress; scale effect; BESO
0 引言
在微/纳尺度技术领域中, 微机电系统 (Micro-Elec ‐ tro-Mechanical System, MEMS) 的结构设计逐渐成为研 究的热点问题。拓扑优化方法由于其能够产生结构的创 新式构型, 可获得比传统的形状和尺寸优化更好的优化 结果而被广泛应用于传统宏观机械结构概念设计中, 成 为机械领域中实现轻量化设计不可或缺的手段。但是在 微观机械结构领域中的发展却较为迟缓。因此, 为了在 MEMS 中实现结构的创新式构型设计, 必须要研究在微 观尺度下的结构拓扑优化方法。
在宏观机械领域, 结构拓扑优化理论与方法逐步完 善, 拓扑优化方法被视为寻求创新结构设计的有力工 具。 S Mantovani 等[1]针对方程式赛车转向柱的设计问题, 提出了一种以质量最小化为目标, 同时遵循严格的结构约束的拓扑优化方法。 Quhao Li 等[2]对于薄壁结构承重构 件的加强筋布局和截面轻量化设计问题, 提出了一种并 行拓扑优化方法, 显著提高了结构的性能, 同时也降低 了计算成本。毕政等[3] 面向如何提升车辆底部防护组件 的抗爆性能, 以降低车身底板变形对车内乘员的威胁问 题, 提出了一种结合混合自动元胞法的拓扑优化设计方 法, 得到了防护组件中加强梁的最佳材料分布形式。同 时, 拓扑优化方法拓宽了其在微观尺度上的应用, 以设 计满足工作需求的微型结构。微机电系统中的结构设计 也需要先进的方法来充分发挥其作用, 因此进行微观结 构的设计显得尤为重要。 Abbas Homayouni-Amlashi 等[4] 为了设计一种从来自不同方向的面内力中获取能量的压 电板能量采集器, 采用拓扑优化方法寻找压电板的最佳 布局, 以最大化电输出并克服电荷抵消。Yi Gao 等[5]考虑微观结构的不确定性, 提出了一种基于可靠性的拓扑优 化框架, 避免了不确定性对所得拓扑体积分数和局部特 征的影响, 实现精确的目标可靠性。此外, 随着材料微 观结构尺寸变小, 非均质材料的有效特性取决于结构尺 寸和材料微观结构尺度的大小, 这种现象称为尺度效应。 众所周知, 一些高阶介质理论, 例如偶应力理论可以提 供合理的方法来解决这个问题, 捕获结构的力学性能和 材料尺度参数, 揭示优化设计中的尺度效应。 Sergey P Pavlov 等[6]在 Timoshenko 运动学假设和修正的偶应力理论 的基础上, 提出了一种基于拓扑优化的纳米梁微观结构 优化方法, 获得了纳米梁在任意静态和动态载荷以及不 同边界条件下的最佳拓扑, 以增加其刚度。 Wenzheng Su 等[7] 为了描述和检验周期性蜂窝状固体微观结构拓扑设 计的尺寸相关性, 以实现结构基频最大化, 在偶应力理 论下建立优化模型, 充分说明了周期性蜂窝状固体微观 结构中优化结果的尺寸依赖性并改进了经典理论在尺度 效应描述方面的弱点。

基 于 变 密 度 (Solid isotropic material with penaliza‐ tion, SIMP) 法的拓扑优化中, 优化过程中会出现数值 问题。如何解决数值问题已成为 SIMP 法优化求解中的重 要组成部分。在这方面, 许多研究者开展了非常有价值 的工作。 Quhao Li 等[8]为了消除固有频率拓扑优化过程中 经常出现的数值问题, 结合“有界公式”和“鲁棒公式”建立了动态拓扑优化公式。 Haitao Han 等[9]提出了一种孔 洞填充方法 (HFM), 用于控制最优结构中孔洞的存在, 不仅限制了最优结构设计中的孔的数量, 而且抑制了棋 盘格和网格依赖现象。与 SIMP 法相比, 双向进化结构优 化 (Bi-directional evolutionary structural optimization, BE ‐ SO) 法允许添加和移除元素, 收敛速度更快, 效率更 高, 得到的优化结构更清晰, 现如今已成为一种寻找最 优解更稳健且更有效的算法。 Mohsen Teimouri 等[10]采用 BESO 法对新的混合实体网格结构进行拓扑优化设计, 显著提高了结构的机械性能。 Yunkai Gao 等[11] 提出了一 种改进的 BESO 法解决多约束拓扑优化问题, 结果表明 不同的约束组合产生不同的材料分布。Xiuyang Qian 等[12] 利用 BESO 法, 对机翼截面进行拓扑优化设计, 以去掉 结构中的低效材料, 证明了拓扑结构的最佳材料布局在 降低应力集中和提高机翼壁板承载能力方面的表现更好。
综上所述, 本文的研究目的是提出一种在微观尺度 下应用 BESO法实施结构拓扑优化设计的方法。基于偶 应力理论而不是经典连续介质理论构建了矩形 8节点偶 应力单元。在此基础上考察了各向同性偶应力介质刚度 最大化的优化结果, 并与相同工况下的经典连续介质结 果进行了对比。数值算例表明, 目前基于偶应力的优化模型详细说明了微型结构设计中优化结果的尺寸依赖性, 并改进了经典优化模型在尺度效应描述方面的弱点。
1 偶应力理论
本文中, ui 为线弹性偶应力模型中的位移矢量, κ i 为独立旋转矢量, χij = κj, i, 为曲率张量。应变张量 εij 依 赖于位移矢量和旋转矢量。应力张量 σ ij 和偶应力张量 mij 通过本构方程与 εij 和χij 存在联系。本节阐述了在偶应力 理论下的基本方程, 其中包括几何方程、平衡方程和本 构方程, 以及广义有限元列式。与经典弹性理论相比, 平面偶应力理论除了原有的 σxx 、σyy 、σzz 、τxy 、τyx 应力 分量外, 新增了 mxz 、myz 两个偶应力分量, 采用符号表 示如图 1 所示。
1.1 基本方程
几何方程:

式中: εij 为应变张量; uj, i 为位移向量; eji 为置换符; κk 为独立的旋转向量; χij 为曲率张量; κj, i 为旋转向量。
平衡方程:

式中: σ ij, i 为应力张量; ψj 为体积力; mij, i 为偶应力张量; eijk 为置换张量; σ ik 为独立的应力张量; φj 为体力偶。
对于平面偶应力问题, 剪应力是对称的, 分别用 τ s 和 τ a 表示, 即 ( τxy ≠ τyx ):

式中: μ 为剪切模量, μ = E / [ 2 ( 1 + δ) ], E 为杨氏模量, δ 为泊松比。
反对称部分 τ a 与刚体局部转角 ω 相关, 并且它不是 一个独立的量, 具体可以表示成如下形式:
式中: λ = D ⋅ δ/ (1 + δ)(1 - 2δ), 为拉梅常数; μ g 为类似 于剪切模量的常数; lg 为材料的特征长度。
1.2 有限元列式
本文研究了矩形 8节点偶应力单元, 其每个节点上 分别有 3个自由度, 如图 2所示, 对于偶应力模型, 根据势能原理, 则单元总势能泛函为:

式中: ui 为单元节点线位移; vi 为节点角位移; ξ 和η 为 局部坐标系中的自然坐标; Ni 为形函数。
Ni 在 8节点单元中分别表示成:

将式 (14) 代入 (13) 取变分, 并使其为 0, 得到 的有限元列式可以简写成如下:

式中: Ke 为单元刚度阵; Ue 为节点位移列向量; Fe 为节 点载荷向量。
依据经典单元矩阵的表现形式, 得出单元刚度矩阵, 即:

2 双向进化结构优化算法
2.1 优化模型
刚度是影响结构能否稳定工作的关键参数, 通常情 况下, 结构优化的最终目的是实现刚度最大化, 也就是 说, 在给定的材料约束条件下, 需要考虑的问题是如何 使结构柔度最小, 以提高抵抗弹性变形的能力。其优化
问题可以定义为如下形式:

式中: c (x) 为平均柔顺性; F T 为力矢量的转置; U 为位 移矢量; K 为总刚度矩阵; Vp 为单个元素的体积; V * 为 规定的总体积; N 为网格中的元素总数; xp 为设计变量, 为了防止刚度矩阵产生奇异问题, 使用较小的 xmin值来表 示空洞元素。
2.2 求解策略
在优化过程中, BESO 法的工作原理与 SIMP 法有所 不同, 它的材料去除方案允许添加或移除材料, 这主要 取决于元素灵敏度数值的大小, 当灵敏度为正时, 添加 材料; 当灵敏度为负时, 移除材料, 同时要通过灵敏度 过滤方案来避免数值不稳定现象的出现。因此, 使用下 式进行滤波:

式中: Q 为设计域中单元的节点总数; bho 为元素中节点 h 和 o 中心的距离; ι o 为灵敏度数; ς (bho )为权重因子。
ς (bho )具体可以写成如下形式:
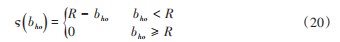
式中: R 为滤波器半径。
式 (20) 表示要将在该滤波半径范围内的元素灵敏 度值作为新的灵敏度数值, 以获得更好的优化结果。
上述灵敏度滤波过程称为空间平滑, 但是存在收敛 问题, 为了保证优化过程的绝对收敛, 引入时间平滑的 概念, 其主要思想是通过取灵敏度的平均值来防止优化 过程中结构性能发生振荡。它可以表示为:

其中 t 和 t -1分别表示当前迭代次数和上一次迭代次 数, 在每次优化过程中, ϕtp = ϕp 将会被用到下一次迭 代。
在 BESO 法中, 为了确定下一次迭代的目标体积,采用如下方程计算:
其中 M 为进化体积比, 当 V > V ∗ 时, 则根据上式计 算并更新得到下一次迭代的目标体积, 当 V < V ∗ 时, 则 结构的体积将在之后迭代中保持不变。
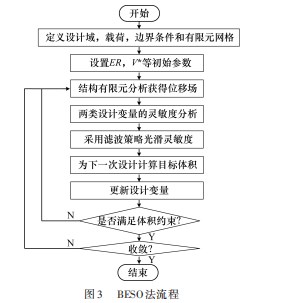
图 3所示为 BESO法的循环流程, 包括确定目标函数 和目标体积约束的详细步骤。
3 数值算例
在这一节中, 分别给出了几个例子来验证方法的可 行性。所有算例均采用的是基于偶应力下的 8 节点矩形 单元求解, 并且假设所有固体材料的杨氏模量为 1, 泊 松比为 0.3, 其进化体积比设为 0.04。
其中ρc (x) 设为 0.5%, ϑ V 设为 0.4%, Z 为整数, 取值 为 5。此外, 如果迭代次数达到 200次, 则优化将被终止。
3.1 算例一
本例模型为长 L=90 mm, 宽 H=30 mm 的 Michell 桁 架, 底部两端固定约束, 并在中间施加竖直向下的载荷, 如图 4所示。将该模型离散化为 90×30个 8节点偶应力单 元, 体积约束为 0.5。首先从图 5所示的变形示意图上可 知, 结构自身各部分的变形程度分配较为平均。符合 Mi‐ chell桁架的工作机理以及微型结构的工作机制。其次,研究了不同尺度下模型的优化结果, 将偶应力材料的特 征长度 lg 与梁高度 H 的比值称为尺度参数, 记为ζ。如表 1 所示, 依次考察了ζ 为 0.1, 0.2, 0.4, 0.6, 0.9 以及 1 时的优化结果。随着ζ 的增加, 优化结果会有明显的差 异。当ζ 在 0.1~0.4之间, 拓扑结构几乎相同, 具体地说, 结构内部的孔洞变得越来越圆滑。当ζ=0.6 时拓扑结构发 生了显著的改变, 孔洞由 2个变为 1个。当ζ=0.9 时, 孔洞彻底消失, 最终得到稳定的结构。应该指出, 当ζ 增 加到与域的维数相当时, 拓扑结构会发生很大的变化。 绘制桁架在ζ=0.6 时的平均柔度、体积分数和拓扑优化的 演变历史, 以研究 BESO 法的质量, 如图 6 所示。通过比 较, 随着体积分数的减小, 平均柔度先增大, 然后在达 到目标体积后收敛到一个几乎恒定的值。经过 48 次迭 代, 最终收敛到稳定的拓扑结构。
3.2 算例二
在这个例子中, 采用长为 L=80 mm、高为 H=30 mm 的悬臂梁作为研究对象, 左端固定约束, 上方承受均布 载荷, 如图 7 所示。宏观设计域离散化为 160×60 个 8 节 点偶应力单元, 材料的体积约束为 0.4。最优构型的变形 如图 8 所示, 最大位移发生在结构上端, 由此可以得出 在微观尺度下悬臂梁的结构设计符合最大刚度要求。同 时为了比较本文采用的 BESO 法和 SIMP 法的优化设计, 在不同尺度下, 应用 BESO 法求解 MBB 梁问题。从表 2中可以看出, 随着尺度参数的增大, MBB 梁的柔度逐渐 变小, 迭代时间和次数减少, 说明尺度的变化会对优化 过程造成影响, 并且宏观尺度和微观尺度下结构的性能有明显的差异。
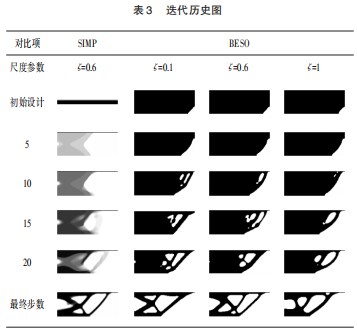
表 3 所示为ζ 取 0.1 、0.6 和 1 尺度下的迭代历史图, 其中 2 列和 4 列为算例模型同一尺度下不同算法的迭代过 程, 可以看出 SIMP 法在迭代过程中会出现灰度单元, 这 一点充分说明了本文采用的 BESO 法比 SIMP 法在数值求 解中稳定性更好。并且该表的 3~5 列反映了材料微观尺 度下结构的特性, 因此偶应力介质拓扑优化具有明显的 尺度效应。随着精密加工工艺的出现, 往往需要设计微 型结构的尺寸或与之配合的构件, 而基于偶应力理论的 拓扑优化方法在这一应用领域表现得更出色。
4 结束语
本文通过将偶应力理论与 BESO 法结合, 针对微型 结构实行最小柔度拓扑优化设计, 事实证明了偶应力介 质下结构存在显著的尺度效应, 解决了经典介质理论无 法得到微观结构的信息, 提供了一种微观结构设计的新 方法。最终的拓扑结果取决于尺度参数的大小, 且不同 尺度下结构的表现形式是不同的, 当尺度参数相差较大 时, 宏观尺度下产生的是桁架结构, 而微观尺度下会出 现不规则的椭圆形孔。并且偶应力介质具有捕获微观结 构信息的能力, 因此尺度效应明显, 这一点是经典连续 介质无法做到的。此外, 与 SIMP 法相比, 本文所用的 BESO 法不会产生灰度单元, 数值稳定性更好。
参考文献:
[1] Mantovani S. Synergy between topology optimization and additive manufacturing in the automotive field[J]. Proceedings of the Insti ‐ tution of Mechanical Engineers, 2021, 235(3):555-567.
[2] Quhao Li. Concurrent topology optimization design of stiffener layout and cross-section for thin-walled structures[J]. Acta Me ‐ chanica Sinica,2021:1- 10.
[3] 毕政,周云波, 吴凯 . 基于拓扑优化的车辆底部防护组件改进 设计[J]. 爆炸与冲击,2021,41(4):152- 162.
[4] Abbas Homayouni Amlashi, Abdenbi Mohand Ousaid,Micky Ra ‐ kotondrabe. Topology optimization of 2DOF piezoelectric under external in-plane force[J]. Journal of Micro-Bio Robotics, 2020 (16):1- 13.
[5] Gao Yi, Liu Yongming. Reliability-based topology optimization with stochastic heterogeneous microstructure properties[J]. Mate ‐ rials & Design, 2021(205).
[6] Pavlov Sergey P, Maksim V Zhigalov. Nonlinear dynamics of to ‐ pologically optimal based on couple-stress theory[J]. University Assets Engineering, 2020(159).
[7] Wenzheng Su, Shutian Liu. Size-dependent microstructure de ‐ sign for frequencies of structures[J]. Structural and Multidisci ‐ plinary Optimization, 2020: 1- 15.
[8] Quhao Li. Topology optimization of vibrating structures with fre ‐ quency band constraints[J]. Structural and Multidisciplinary Op ‐ timization, 2020: 1- 16.
[9] Haitao Han. Topological constraints in 2D structural topology op ‐ timization[J]. Structural and Multidisciplinary Optimization, 2020(63):1-20.
[10] Teimouri Mohsen, Mahbod Mahshid. Topology-optimized hy ‐ brid solid-lattice structures for efficient mechanical perfor ‐ mance[J].Structures, 2021(29):549-560.
[11] Gao Yunkai. Bi-directional Evolutionary Structural Optimiza ‐ tion of Structures with Constraints[J]. IOP Conference Series, 2020(746):012043.
[12] Xiuyang Qian. Structural design of composite stiffened panel for a flat wing micro-aircraft[J]. SN Applied Sciences, 2020, 14(2):767-773.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/45772.html