SCI论文(www.lunwensci.com)
摘 要:在传统分布式计算平台中,任务的调度是单纯基于机器资源的剩余价值,如果在超大规模机器集群下,机器彼此 间可被调度的价值差会趋于连续,那么以上调度规则会随着样本基数变大而出现调度不均匀等问题。针对这种情况,提出仿红 黑树拓扑的分布式计算平台框架设计。设计首先模拟红黑树拓扑结构,然后基于机器资源的计算资源能力,最终形成多维度调 度算法,解决大规模机器集群散列的充分性。实验结果表明,设计能够有效增强平台的综合调度能力,在分布式计算等领域能 够带来一定的实际作用。
关键词:红黑树,分布式,计算平台
Framework Design of Distributed Computing Platform Based on Red-black Tree Topology
WANG Lei1. QIAN Baochao2. CHEN Lin3
(1.Nanjing Satisfactory Digital Technology Co., Ltd., Nanjing Jiangsu 210000; 2.General Technical Machine Tool
Research Institute Shanghai Branch, Shanghai 200000; 3.Library Department, Nanjing Polytechnic Institute, Nanjing
Jiangsu 210000)
【Abstract】:In the traditional cycle computing platform, the scheduling of tasks is completely based on the residual value of machine resources. If under the super-large-scale machine load, the schedulable value difference of the machine will tend to be continuous, then the above scheduling rules will be the sample base becomes larger and problems such as uneven scheduling appear. Aiming at this situation, a framework design of topology computing platform imitating red-black tree topology is proposed. Firstly, a simulated red-black tree topology is designed, and then based on the computing power of machine resources, a multi-dimensional scheduling algorithm is finally formed to solve the adequacy of large-scale machine cluster hashing. The experimental results prove that the design can effectively enhance the comprehensive scheduling capability of the platform, and it can bring certain practical effects in fields such as multi-dimensional computing.
【Key words】:red-black tree;distributed;computing platform
引言
当前云计算与大数据发展迅猛,人工智能与机器学 习历经多年再次成为前沿热门技术,科技的突破成为推 动社会生产力变革的有力抓手,然而数据、算力的发展 离不开分布式计算技术的进步和有效使用。传统的分布 式计算平台往往采用硬件计算资源为单一考量,去完成任务与计算资源的匹配。在计算集群规模较小的情况 下,机器的差异会被放大,这一策略可以保障调度的有 效性,但是随着人工智能与算力的不断强大,机器资源 的规模将指数级别增长。在这一背景下,个体间的差异 会极端的缩小,所以采用一种能满足散列充分性的合理 算法至关重要。
红黑树 [1] 是一种高度稳定的时间复杂度 [2] 为 O(logn) 的二叉查找树,能够通过旋转和变色来保持特性,设计 通过实现红黑树结构与机器计算资源结合的多维度算 法,去解决大规模集群分布式计算平台的调度问题。同 时本文也在主从节点职责边界划分、节点选举、红黑树 算法等方面系统地去完成分布式平台的模块化设计。最 后为了验证本设计的科学有效性,通过大规模的充分取 样实验进行了回溯验证,同时也检测调度算法的性能。 实验表明,设计可以有效改善大规模集群调度的分散 性,提升调度的性能。
1 仿红黑树拓扑的分布式设计
1.1 分布式任务与分布式平台的说明
分布式任务 [3] 往往是要面对海量数据的快速处理 或是对任务处理有着超高的时效要求,所以分布式任务 一般需要多实例并发执行。如果任务设定的并发执行实 例数为 n,那么这 n 个实例需要在一个机器计算集群上 执行,假设机器资源数目为y,那么为了合理利用计算 资源,我们需要尽可能地将 n 个任务实例均匀地散落在 y 个机器资源节点上,否则极有可能出现部分机器资源 执行任务实例太多,而导致机器性能负载过高以至于机 器执行卡顿,同时部分节点过于空闲,这种非均匀合理 的资源调度情况。传统的求余算法、Hash 散列 [4] 算法 具有一定的作用,去保障任务与资源的合理调度,但存 在调度规则自动化程度不高,需要事前提前参与规划规 则。本文将采用一种数据结构稳定、性能优异的红黑树 拓扑去解决资源调度问题。
1.2 分布式计算平台中的红黑树拓扑的定义
首先,我们假设将分布式计算平台的机器资源数量 设置为y,每台机器对应 [0. y) 中连续整数数值的一个。 然后想在这个分布式计算集群上创建一个任务,并且该 任务的并发执行实例数设置为 n。那么并发数为 n 的该 任务在机器资源数量为y 的集群上执行,需要从无到有 地创建一个该任务对应的红黑树。
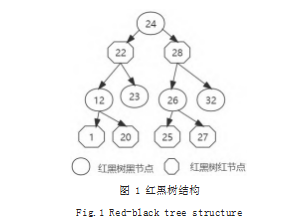
红黑树是一种平衡二叉树 [5],当节点出现新增或者 删除时,通过节点旋转、变色等手段去维护数据结构的 稳定,保持红黑树特有的特性。红黑树具备以下性质 : 结点是红色或黑色 ;根结点是黑色 ;所有叶子都是黑 色 ;每个红色结点的两个子结点都是黑色 ;从任一结点 到其每个叶子的所有路径都包含相同数目的黑色结点。 如图 1 所示。
本仿红黑树拓扑的分布式计算平台设定,每个任务 都需要生成唯一对应的一个红黑树拓扑,同时,红黑树 中黑色节点为最终任务执行节点,红色节点为非任务执行节点。同时,红黑树拓扑中的每个节点,包含以下信息 :随机生成的节点数值、机器资源编号、颜色为红色或者黑色、左右子树索引。每个节点的值为随机生成的数字 ;机器资源编号从 1 到y 循环取出,如果当次插入节点的机器资源编号为 z,且 z<
y,那么下次节点的资源编号为
z+1 ;树中节点的颜色是否为红色 ;每个节点的左右子树根节点的索引。节点内容如表 1 所示。
1.3 红黑树拓扑的作用
红黑树本质上来说就是一棵二叉查找树,但它在二 叉查找树的基础上增加了着色和相关的性质使得红黑树 相对平衡,从而保证了红黑树的查找、插入、删除的时 间复杂度最坏为 O(logn)。每个节点都携带集群资源的 信息,红黑树又是一颗平衡树,从任一节点到其每个叶 子的所有路径都包含相同数目的黑色结点,以上特性可 以保证任务的实例会非常均匀地散落在机器资源上。
1.4 创建任务对应的红黑树拓扑并进行调度
任务在平台新建后,将开始创建该任务对应唯一的 红黑树拓扑。红黑树拓扑中,每次插入一个节点后,平 台会记录树中黑色节点的总数量,假设数量为 x,同时 任务设定的并发数为 n,如果黑节点数量 xn,则取出所有的黑色节点列表,并随机取出其中的 n 个 ;平台将根据该批黑色节点的集群机 器编号确定实例执行的位置。
1.5 基于红黑树拓扑与机器资源多维调度算法
红黑树拓扑调度具备良好的分散性,但是单纯依赖 红黑树拓扑进行资源调度存在一定的局限性,计算平台 本质上是基于计算资源的调度,将任务与机器资源合理 分配,尽可能发挥出最大的利用价值。本计算平台基于 拓扑与机器初始资源、机器可用资源以及手动机器节点 选择四大维度进行综合调度,不同的维度所占优先级不 同,平台会进行综合计算。调度机器资源的初始配置比 如 CPU、内存、磁盘,机器资源实时可用资源情况比 如可用内存、可用磁盘、剩余 CPU。首先在生成红黑 树拓扑的时候,保证生成的黑色执行节点数目 x 是用户 设定的任务并发数目 n 的两倍,然后循环迭代黑色节点 列表,取出黑色节点所在的机器资源,每台机器的初始 性能配置分级别归类,不同级别对应的加权分数不同, 配置越高分值越高,同理,机器不同剩余可用资源也要 进行分级,并且对应不同的分值。计算所有的黑色节点 列表的总分支,并进行分值降序排序,在 x 个黑色列表 中取出前 n 个黑色节点最终作为任务调度执行节点。
1.6 红黑树拓扑的动态性
当任务在分布式计算平台新建后,平台会生成与任 务对应的唯一红黑树拓扑结构,平台机器资源会按照红 黑树拓扑的结果进行生成任务执行实例。但是拓扑并不 是一成不变的,如果计算平台的机器资源出现宕机等异 常情况导致该台机器不可用,那么机器集群要将该台资 源进行剔除。同时任务的所有并发实例都需要平滑结束 进程,此时需要按照红黑树拓扑规则重新建立一个新拓 扑,分布式计算平台再按照新拓扑重新进行任务实例的 资源调度与执行。
与剔除机器节点略有不同的是,如果分布式平台的 机器集群新增计算机器节点,可以重新生成红黑树拓扑 然后进行任务重新资源调度与计算,也可以选择不进行 拓扑重建,仍按原有的拓扑进行执行,尽可能地减少任 务重新调度计算带来的资源消耗,所以平台在任务创建 时对这种场景可以进行选择配置,保持原有拓扑调度还 是重新新建拓扑调度。
2 分布式计算平台的架构设计
2.1 分布式计算平台的整体架构
2.1.1 架构
分布式计算平台以主从 [6] 模式架构对整体进行管 理,主节点 Master 负责集群资源管理、任务的拓扑管 理、任务与资源调度、平台 Metrics 统计等,具体涵盖集群节点处理器 ClusterNodeHandler、拓扑任务处理 器 TopologyHandler、资源调度与分配处理器 Schedule Handler、哨兵 [7] 处理器 SentinelHandler、平台 Metrics处理器 MetricsHandler 等核心模块。从节点 Slave 主要根 据主节点的调度去负责任务实例的构建、监控、销毁等管 理,另外需要对机器进行基本的监控,并及时将机器节点 运行情况与任务的执行情况上报给主节点。从节点 Slave 具体涵盖集群节点处理器 ClusterNodeHandler、任务 处理器 TaskHandler、哨兵处理器 SentinelHandler 等 核心模块。同时每个从节点还要在主节点进程异常、主节 点所在机器宕机等情况下参与主节点的竞争选举,以保证 主从架构的完整性,从而维持平台的高可用性。平台以框 架执行器 Executor 为核心单元,框架执行器 Executor 会在集群中每个计算机器节点进行部署安装,主节点、 从节点除了哨兵处理器外其他各自拥有的核心处理器都 会封装到框架执行器中。通过各模块协同组合,共同支 撑分布式计算集群的运转,保证任务在集群之上能够高 效稳定地执行。整体架构如图 2 所示。
2.1.2 集群节点处理器
集群节点处理器是分布式计算平台中主从节点都含 有的处理器,类似于集群中每台机器上的中枢大脑,主 要负责与本节点上其他类处理器进行协作调度,并负责 与主节点机器进行通信,从而共同组建一个分布式计算 框架集群。它需要对所在机器上的 CPU、内存、磁盘 等信息实时监控,对主节点分配的任务安排对应的其他 处理器去执行,并随时将管辖的所有处理器的执行情况 进行上报。
2.1.3 拓扑任务处理器
拓扑任务处理器是主节点拥有的处理器,一个任务 的创建必定首先伴随着任务红黑树拓扑的创建,然后才 能进行综合资源调度,任务实例的消亡也对应红黑树拓 扑的消亡。
2.1.4 资源调度与分配处理器
资源调度与分配处理器也是主节点拥有的处理器,负责资源的计算与调度,它与拓扑任务处理器协作,基 于红黑树拓扑与机器资源多维调度算法去执行调度的核 心模块。
2.1.5 哨兵处理器
哨兵处理器是主从节点都包含的处理器,它是独立 于框架执行器之外的单独进程。一方面哨兵监控机器上 框架执行器进程,如果是从节点出现宕机、进程异常情 况导致框架执行器无法自身向主节点上报数据时,哨兵 可以完成这一任务,机器集群可以剔除问题主机 ;另一 方面哨兵也与其他机器上哨兵通信,在主节点宕机、主 节点进程异常时重新选举主节点。
2.1.6 任务处理器
任务处理器为从节点上专有的模块,主要负责按照 主节点调度对任务进行生命周期管理,同时监控任务执 行情况。
2.1.7 平台 Metrics 处理器
平台 Metrics 处理器为主节点上的模块,采集各从 节点所在机器上的各类监控指标,包含从节点运行情况、 任务实例执行情况等主要信息,最终形成数据大屏。
2.2 集群主节点选举算法
2.2.1 哨兵监控机器节点
平台中主节点只有一个,并且主节点不执行具体 的实例任务,只负责集群控制调度。每个哨兵都会定期 10s 检测主、从节点的进程状态, 状态有健康、亚健康、 疾病三种状态,系统启动后各节点默认为健康状态。如 果出现单个哨兵连续三次检测节点未及时回复,该哨兵 会将标记该台节点为亚健康状态,同时记录该节点亚健 康巡检哨兵数 m 为 1.同时信息上报给哨兵集群,如果 出现其他哨兵连续三次检测也未及时回复, m 将进行加 一操作,当 m 大于哨兵集群中一半的数量,系统正式标 记该台节点为疾病状态。如果该台疾病状态节点是从节 点,那么机器集群将剔除该台机器,所涉及的任务主节 点将重新调度。如果该台疾病状态节点是主节点,分布 式计算集群将重新进行主节点选举。
2.2.2 主节点选举算法
平台采用了类 Raft[8] 算法思想进行主节点选举,即 少数服从多数。考虑到主节点不执行具体实例任务,所 以平台如果主节点是疾病状态后,选举将优先推举那些 任务数量少、机器资源整体配置低的节点,因为主节点 不需要执行繁重的任务实例,这与任务调度稍有不同。 选举的过程中,首先将健康状态的节点按照执行任务数 量进行降序排序,第一名得分 1 分,第二名得分 2 分, 依次类推, 同时任务数量得分系数为 0.7.再将健康状态的节点按照整体配置降序排序,配置越高靠前排序, 第一名得 1 分,第二名得 2 分,依次类推,同时机器整 体配置得分系数为 0.3.最后迭代计算出所有健康状态 节点的加权总分,前三名为主节点备选节点。此时,循 环备选节点列表,如果哨兵集群中超过一半的哨兵连续 三次对该备选节点所在机器以及机器上所在哨兵进行通 信状态确认,则最先获得认可得当选为集群主节点。
2.2.3 主节点切换后的资源迁移
当通过选举算法确定好新主节点后,涉及到一些数 据与组件变动。第一部分是主节点上原有的任务实例需 要进行迁移,由于主节点选举优先任务少的从节点,所 以此时新主节点上的任务迁移工作量以及资源消耗相对 可控。第二部分是作为主节点所必需的任务拓扑处理 器、资源调度与分配处理器、平台 Mertrics 处理器都 需要创建,同时原有的任务处理器需要关闭。
2.3 红黑树常规算法的实现
算法 1 红黑树节点左旋算法。
def left_tree_node_rotate(self, x):
y = x.right_tree_node
x.right_tree_node = y.left_tree_node
ify.left_tree_node != self.Nil:
y.left_tree_node.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.left_tree_node:
x.parent.left_tree_node = y
else:
x.parent.right_tree_node = y
y.left_tree_node = x
x.parent = y
算法 1 中,函数输入为需要左旋节点,首先将节点 的右子树赋值保存,左子树直接设置为右子树。如果右 子树y 的左子树不为 nil 节点, 则y 的左子树父节点为 函数输入节点 x, y 的父节点为 x 的父节点。如果 x 父节 点为空,则根节点为y。如果 x 等于 x 的父节点的左子 树节点,则 x 的父节点的左子树节点为y,否则 x 的父 节点的右子树节点为y。最后 y 的左子树为 x, x 的父节 点设置为y。
算法 2 红黑树节点右旋算法。
def right_tree_node_rotate(self, x):
y = x.left_tree_node
x.left_tree_node = y.right_tree_node
ify.right_tree_node != self.Nil:
y.right_tree_node.parent = x
y.parent = x.parent
if x.parent == None:
self.root = y
elif x == x.parent.right_tree_node:
x.parent.right_tree_node = y
else:
x.parent.left_tree_node = y
y.right_tree_node = x
x.parent = y
算法 2 中,函数输入为需要右旋节点 x,节点右旋 算法同左旋算法相反。
算法 3 红黑树节点插入算法。
def insert(self, key, machine_id_num): node = Node(key)
node.parent = None
node.tree_node_value = key
node.left_tree_node = self.Nil
node.right_tree_node = self.Nil
node.color = 1
node.machine_id_num = machine_id_num
y = None
x = self.root
while x != self.Nil:
y = x
if node.tree_node_value < x.tree_node_value:
x = x.left_tree_node
else:
x = x.right_tree_node
node.parent = y
ify == None:
self.root = node
elif node.tree_node_value < y.tree_node_value:
y.left_tree_node = node
else:
y.right_tree_node = node
if node.parent == None:
node.color = 0
return
if node.parent.parent == None:
return
self.fix_insert(node)
算法 4 红黑树节点插入平衡算法。
def fix_insert(self, k):
while k.parent.color == 1:
if k.parent == k.parent.parent.right_tree_node: u = k.parent.parent.left_tree_node
if u.color == 1:
u.color = 0
k.parent.color = 0
k.parent.parent.color = 1
k = k.parent.parent
else:
if k == k.parent.left_tree_node:
k = k.parent
self.right_tree_node_rotate(k)
k.parent.color = 0
k.parent.parent.color = 1
self.left_tree_node_rotate(k.parent.parent) else:
u = k.parent.parent.right_tree_node
if u.color == 1:
u.color = 0
k.parent.color = 0
k.parent.parent.color = 1
k = k.parent.parent
else:
if k == k.parent.right_tree_node:
k = k.parent
self.left_tree_node_rotate(k)
k.parent.color = 0
k.parent.parent.color = 1
self.right_tree_node_rotate(k.parent.parent) if k == self.root:
break
self.root.color = 0
2.4 仿红黑树调度算法的实验精度
基于红黑树调度算法在不同机器规模的集群上的表 现情况,将通过以下算法 5 进行实验。如果一次任务调 度,实例任务均匀的分散到各台集群中的机器上,可以 判定这是一次良好的资源调度行为。在实际的科研、生 产中,绝对均匀是很难实现。算法 5 中机器节点数为 y,黑色执行节点代表的任务数为 x,经过一次调度后, 每台机器上都分配了 x 中的一部分任务,找出分配任 务数最多的机器,并计算出任务占总任务数 x 的占比为max,同时找出分配任务数最少的机器,算出任务占比 为 min,规定 max-min 的结果为精度差。
在算法 5 中实验将以机器规模、精度差、一次实验 需要测试精度的次数、每次需要的红黑树数量、每颗红 黑树节点数量为 5 个输入变量,从而计算出调度算法的 表现。
算法 5 红黑树节点插入平衡算法。
def perform_try(
machine_x,
accuracy_error,
a_try_times,
a_try_time_tree_num,
a_try_time_tree_node_random_num): for o in range(a_try_times):
tree_list = []
for z in range(a_try_time_tree_num):
rb = RedBlackTree()
x = 0
# num of rb-tree node
node_y = machine_x * random.uniform( 0.a_try_time_tree_node_random_num)
for y in random.sample(range(0. 1000000000), math.floor(node_y)):
x = 0 if x >= machine_x else x
rb.insert(y ,x)
x = x + 1
rb.print_tree()
# print(len(rb.blackNodes))
tree_list.append(rb)
# print(len(tree_list))
low = 0
for tree in tree_list:
black_machine_arr = []
for node in tree.blackNodes:
black_machine_arr.append(
node.machineIdNum)
# print(black_machine_arr)
dict = {}
for black_num in black_machine_arr:
dict[black_num] = dict.get(black_num,0) + 1 # print(dict)
#-min(dict.values())/sum(dict.values())) if len(dict) >0 and
(max(dict.values())/sum(dict.values()) -min(dict.values())/sum(dict.values()))
> accuracy_error :
low = low + 1
print(" 匀散波动误差小于 "
+ str(accuracy_error * 100)
+ "% 的稳定性为 :"
+ str((1-low / len(tree_list))*100) + "%")
3 实验
仿红黑树拓扑调度算法的实验主要围绕分布式集群 下的任务调度情况进行开展,任务资源调度的优良评价 以匀散精度差小于规定值并且保持 100% 稳定为成功, 实验围绕算法 5 进行开展。
3.1 资源调度的匀散精准差小于 1% 的实验
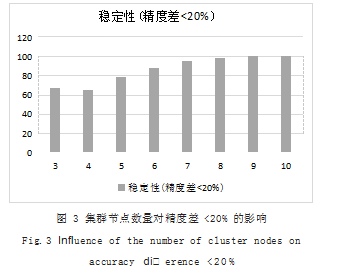
设定 perform_try 函数的参数 (y,0.2.100.100. 5), 即y 台机器组成的集群、保证每次调度误差在 20% 以内,每次实验要用 100 次测试论证,每次测试论证要 随机生成 100 个红黑树任务拓扑,同时每颗树的节点为 [0. 5×100) 内随机的整数。本函数按照以上参数预计 总共会执行y×100×250 次实验运算。
经过测试,要想保证调度的误差在 20% 以内,不同 的y 值那么算法的稳定性结果不同,实验如图 3 所示。
通过实验发现,如果集群节点数大于等于 10 可保 证精度差小于 20% 是 100% 稳定的。
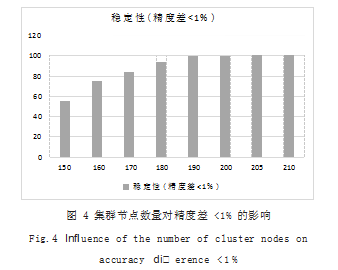
此时将精度差设定为 1%, 通过重新设定函数参数 perform_try(y, 0.01. 100. 100. 5),实验如图 4 所示, 通过实验发现,如果集群节点数大于等于 210 可保证精 度差小于 1% 是 100% 稳定的。
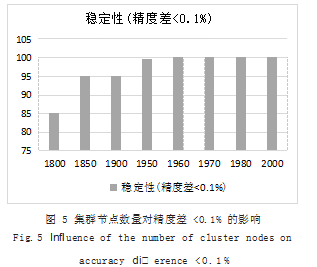
3.2 资源调度的匀散精准差小于 0.1% 的实验
此时将精度差设定为 0.1%,通过重新设定函数参数 perform_try(y,0.001.100.100.5), 实验如图 5 所示, 通过实验发现, 如果集群节点数大于等于 2100 可保证精度差小于 0.1% 是 100% 稳定的。
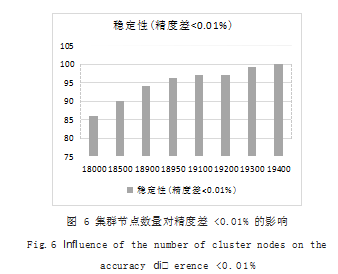
3.3 资源调度的匀散精准差小于 0.01% 的实验
此时将精度差设定为 0.01%,通过重新设定函数参 数 perform_try(y, 0.0001. 100. 100. 5),实验如图 6 所示, 通过实验发现, 如果集群节点数大于等于 2100 可保证 精度差小于 0.01% 是 100% 稳定的。
4 结语
采用一种仿红黑树拓扑结构来设计和实现分布式 计算平台,借助计算机体系中性能极为优秀的数据结 构,加上高可用的分布式计算系统的设计,来解决资源 调度的问题,特别是在规模化的计算集群中,可以非常巧妙地解决散列不均和散列维度单一的问题。同时尝试 研究了不同精度差下的调度表现与机器集群规模之间的 关系,通过多轮大规模实验,探索出各自的节点数量临 界点。本分布式计算平台可以为科研和生产提供有益指 导,在算力、大模型 [9] 等当前技术的浪潮下具备较强的 实用价值。
参考文献
[1] 杨勇.基于图元文件实现红黑树插入删除过程的动态演示 [J].电脑知识与技术,2021.17(35):166-168+174.
[2] 傅晓航,郑欢欢.K分搜索的时间复杂度分析[J].计算机技术 与发展,2021.31(2):175-179.
[3] 俞珍秒,汪明贵.浅谈分布式任务注册及调度的实现方法[J]. 中国设备工程,2021(8):51-52.
[4] 许旭晗,张俊杰,陈彦昊,等.TOE Hash冲突处理设计与实现 [J].工业控制计算机,2023.36(3):79-81.
[5] 杨云峰,胡金燕,王玉学,等.二叉树遍历算法的教学设计与实 践[J].电脑与信息技术,2023.31(3):51-54.
[6] 董文文,郭志亮,吉祥钻,等.一主多备集群式控制器设计与实 现[J].福建电脑,2020.36(10):9-13.
[7] 杨土超,章超,赖瑞福,等.一种基于振动传感器开发的哨兵模 式[J].汽车电器,2022(12):43-46.
[8] 胡琪,王晓懿,贺国平.基于Raft协议的两节点主备系统调度 算法[J].软件导刊,2022.21(4):109-115.
[9] 熊子晗,李雨轩,陈军,等.大模型发展趋势及国内外研究现状 [J].通信企业管理,2023(6):6-12
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/64903.html