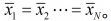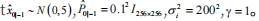SCI论文(www.lunwensci.com):
摘 要:针对无线传感器网络稀疏信号重构问题,提出了一种基于嵌入伪测量的平方根无迹卡尔曼一致滤波 (SRUKCF) 的 分布式稀疏非线性信号重构算法。融合来自无线传感器网络中不同节点的随机线性测量值,使各滤波器对稀疏非线性信号的估 计达到一致。仿真结果验证了该算法的有效性。
关键词:无线传感器网络 ;卡尔曼一致滤波 ;压缩感知 ;重构算法
An Optimized Algorithm of Consensusbased Kalman Filtering with Distributed Sparse Signal Reconstruction
ZHANG Zhaoxia, LI Lixia, LUO Zhiyong, LIU Jiping
(School of Automation and Information Engineer, Hunan Chemical Industry Vocation Technology College, Zhuzhou
Hunan 412004)
【Abstract】: In order to deal with the problem of sparse signal reconstruction for wireless sensor networks (WSNs), an distributed sparse signal reconstruction Optimized algorithm based on square root unscented kalman consensus filter (SRUKCF) with embedded pseudo-measurement is proposed in this paper. By fusing the random linear measurements from different nodes in the WSNs, such that all filters can reach a consensus on the estimate of sparse nonlinear signals. The simulation results show that the Optimized algorithm is effect.
【Key words】: wireless sensor network;consensusbased kalman filtering;compressive sensing;reconstruction algorithm
0 引言
近年来,许多研究人员尝试在经典的信号估计框架 中处理稀疏信号重构问题,如卡尔曼滤波。文献 [1] 中基 于卡尔曼滤波的压缩感知的第一次成功尝试被提出。文 献 [2]Carmi 等人将 1 范数约束作为伪测量 (PM) 集成到 经典的 2 范数卡尔曼滤波框架中,用于恢复可能时变的 稀疏信号。文献 [3] 提出了一种基于分层概率模型的算 法,该算法以重加权 1 范数最小化为核心计算,类似于 经典的卡尔曼滤波,通过时间传播二阶统计量。综上所述,这些工作几乎都考虑了线性信号。因此,本算法利 用几个来自无线传感器网络的随机线性测量开发一种分 布式滤波方法来重建稀疏非线性信号。综合考虑了基于 平方根无迹卡尔曼一致滤波和伪测量技术形成了该方法。
1 卡尔曼滤波稀疏信号估计
1.1 稀疏信号恢复
基于卡尔曼滤波框架,一般的非线性估计方法包括 扩展卡尔曼滤波 (EKF) 和无迹卡尔曼滤波 (UKF)。EKF 利用了在高阶 CS 系统中很难得到的Jacobian 矩阵。非 线性系统的线性化往往会引入误差,容易导致系统发散。
这里,考虑一个稀疏的 - 值随机离散时间过程 R
n、
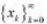
,其 中,x
k 为 s- 稀疏,如果‖x‖
0=s 。 假设 x
k 按 照以下动态模型变化。

其中 A
k ∈ R
n×n 为状态转移矩阵,
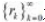
为零均值 白色高斯序列,具有协方差 R
k ≥ 0。的 m 维线性测量, 当 m < n,从测量中恢复信号通常是一个病态问题。x
k可以通过求解以下优化问题精确恢复。

但式 (3) 是一个 NP 问题,不能有效求解。但根据文献 [4],如果测量矩阵服从 RIP,则可以通过求解下面 的凸优化问题得到式 (3) 的解。

对于 R
n 中的 s 稀疏信号,只需要在样本 m=slogn 的顺序上重建。
1.2 嵌入伪测量卡尔曼滤波
对于式 (1)(2) 中给出的系统,卡尔曼滤波可以提供 xk 的一个估计,该估计是下面 l2 无约束极小化问题的一个解。

在文献 [2] 中讨论了式 (4) 的随机情况。

和它的对偶问题。

通过构造一个伪测量方程

其中,
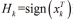
和
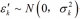
作为虚拟的测量噪 声,式 (7) 约束优化问题可以在卡尔曼滤波的框架下求 解,被归纳为 CSKF-1) 法 [3]。
在伪测量方程中,测量矩阵 H
k 是与状态相关的, 可以用表示。这种近似的发散性已由文献中 的定理 1 讨论。σ
k 是一个可调参数,它决定了状态估计 x
k 约束的严密性 l
1。
2 SRUKCF-PM 稀疏信号重构
考虑一个传感器网络,其拓扑结构由无向图 G(V,E,A) 表示。图中有节点集 V=(1,2,…,N)、边集 E=V×V 和具有 非负邻接元素 a
i,j 的邻接矩阵 A=[a
i,j]。j 节点称为 i 节点 的邻居,用 N
i 表示。假设 G 是联通的。对于非线性动 态系统,其动态系统、信号和测量满足以下模型。

假设传感器节点 i 的测量符合线性模型。
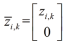
,
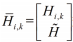
和
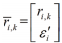
. 可以得到节点 i 的测量方程。

其中,H
i,j 是节点 i 的测量矩阵,r
i,j 是 R
i,j 零均值高斯白噪声的协方差,
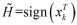
, 是服从 N(0,σ
i2) 的 虚拟测量噪声。设定
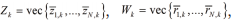
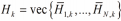
和

,可以得出 :

基于 {Z
1,… ,Z
k} 的卡尔曼滤波器的状态估计可表征为 :

估计误差协方差矩阵的逆矩阵,又称信息矩阵。其中,
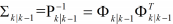
和
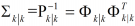
和分别表示

和
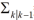
和的 Cholesky 因子。根据卡尔曼 滤波的信息形式,定义 :

其中

可得 :

其中

和

分别表示 Cholesky 因子分 解和 Cholesky 因子更新。
来自卡尔曼滤波的状态估计为

时间更新为

其中
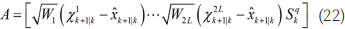
其中
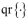
为 QR 分解,

和加权点
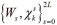
为

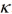
为一个比例因子。式 (15)-(24) 定义了嵌入伪测量的SRUKCF。由式 (16) 和式 (17) 可以看出,引入伪测量方程后,
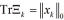
状态的稀疏性对状态误差协方差的演化产生了影响。如第二节所述,将

近似为

我们可以在网络中每个节点上嵌入伪测量,构造如下的 SRUKCF :
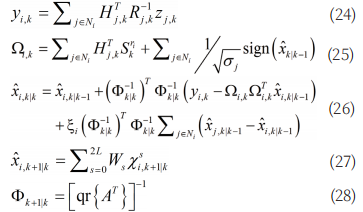
式
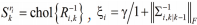
中 γ 是一个可调参数,决定了一致性更新的权值,使得误差动态全局渐近
稳定,所有滤波器在状态估计上渐近一致,也就是说
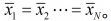
假设全局感知矩阵 Hk 满足约束等距性,通过传感器网络获得 m 维全局测量 Z
k。重要的是,对于网络中的任何一个节点,对其测量的维数没有限制,这意味着它可以小于 slogn 下界。
3 实验仿真
在本部分中将进行一些仿真实验并分析得到的结果。使用本文提出的算法对一个稀疏信号进行估计,所有的测量值都是通过一个分布式 WSN 得到的。在不失一般性的前提下,我们考虑一个如图 1 所示的 6 个节点的 WSN,其拓扑由一个无向图 G=(V,E,A) 表示,图中有节点集 V={1,2,3,4,5,6}、边集 E={(1,2),(1,3),(2,4),(3,5),(3,6),(4,5),(5,6)} 和邻接矩阵 :

在第一个实验中,首先进行参设设置对系统进行模拟, 具体设置为 :m=72,s=10,n=256,Q(i,i)=3
2,Rk=0.25
2 ×
I
12×12。这个过程可以用式 (32) 描述。

其中 i ∼ U
i [1,256],72 维测量值是通过网络获得的。假设每个节点都可以得到一个 12 维的测量值,也就是说,
H
i ,k ∈ R
12×256 是由高斯分布 N (0,1/72) 得出的,设置
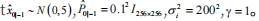
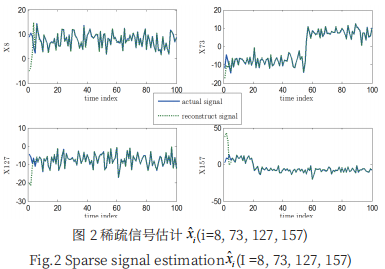
图 2 给出了对 1 号传感器节点 x8、x127、x157 的时 变实际信号的估计。很明显,1 号传感器节点对支架上 的实际信号给出了满意的估计。此外,采用了归一化均 方误差 (NMSE) 来评价各传感器节点的误差性能。
 4 结论
4 结论
能耗均衡是无线传感器网络的重点应用之一,稀疏 信号重构的使用有效改善了无线传感器网络中的能量约 束问题。本文利用基于能量均衡的压缩感知理论,将平 方根无迹卡尔曼滤波器与一致性算法相结合。同时,在 滤波器中引入伪测量方程来处理信号的稀疏性。相对于 一般稀疏信号重构算法而言,SRUKCF-PM 提供了令人 满意的稀疏非线性信号估计,使用远少于传统所需的测量 ;同时,本文的算法有效可以延长无线传感器网络的生命周期。
参考文献
[1] N.Vaswani.Kalman filtered compressed sensing.In Proc.of IEEE Int.Conf.on ImageProcessing (ICIP),Oct.2008: 893-896.
[2] A.Carmi,P.Gurfil,and D.Kanevsky.Methods for sparse signal recovery using kalman filtering with embedded pseudo-measurement norms and quasinorms.IEEE Transactions on Signal Processing,2010,58(4):2405-2409.
[3] Haiyang Yu,et al.Distributed sparse signal estimation in sensor networks using consensus filtering.IEEE/CAA
Journal of Automatica Sinica,2014,1(2):149-154.
[4] Candes E J,Romberg J and Tao T.Robust uncertainty principles:exact signal reconstructionfrom highly incomplete frequency information.IEEE Transactions on Information Theory,2006,52(2):489-509.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/34309.html

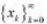 ,其 中,xk 为 s- 稀疏,如果‖x‖0=s 。 假设 xk 按 照以下动态模型变化。
,其 中,xk 为 s- 稀疏,如果‖x‖0=s 。 假设 xk 按 照以下动态模型变化。
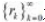 为零均值 白色高斯序列,具有协方差 Rk ≥ 0。的 m 维线性测量, 当 m < n,从测量中恢复信号通常是一个病态问题。xk可以通过求解以下优化问题精确恢复。
为零均值 白色高斯序列,具有协方差 Rk ≥ 0。的 m 维线性测量, 当 m < n,从测量中恢复信号通常是一个病态问题。xk可以通过求解以下优化问题精确恢复。 





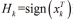 和
和 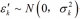 作为虚拟的测量噪 声,式 (7) 约束优化问题可以在卡尔曼滤波的框架下求 解,被归纳为 CSKF-1) 法 [3]。
作为虚拟的测量噪 声,式 (7) 约束优化问题可以在卡尔曼滤波的框架下求 解,被归纳为 CSKF-1) 法 [3]。
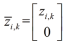 ,
,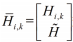 和
和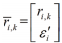 . 可以得到节点 i 的测量方程。
. 可以得到节点 i 的测量方程。
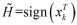 , 是服从 N(0,σi2) 的 虚拟测量噪声。设定
, 是服从 N(0,σi2) 的 虚拟测量噪声。设定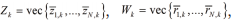
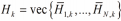 和
和 ,可以得出 :
,可以得出 :

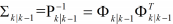 和
和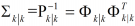 和分别表示
和分别表示  和
和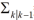 和的 Cholesky 因子。根据卡尔曼 滤波的信息形式,定义 :
和的 Cholesky 因子。根据卡尔曼 滤波的信息形式,定义 :
 可得 :
可得 :
 和
和 分别表示 Cholesky 因子分 解和 Cholesky 因子更新。
分别表示 Cholesky 因子分 解和 Cholesky 因子更新。

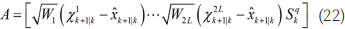
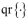 为 QR 分解,
为 QR 分解, 和加权点
和加权点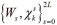 为
为
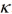 为一个比例因子。式 (15)-(24) 定义了嵌入伪测量的SRUKCF。由式 (16) 和式 (17) 可以看出,引入伪测量方程后,
为一个比例因子。式 (15)-(24) 定义了嵌入伪测量的SRUKCF。由式 (16) 和式 (17) 可以看出,引入伪测量方程后,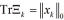 状态的稀疏性对状态误差协方差的演化产生了影响。如第二节所述,将
状态的稀疏性对状态误差协方差的演化产生了影响。如第二节所述,将  近似为
近似为
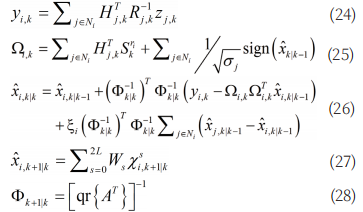
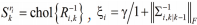 中 γ 是一个可调参数,决定了一致性更新的权值,使得误差动态全局渐近
中 γ 是一个可调参数,决定了一致性更新的权值,使得误差动态全局渐近