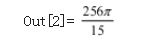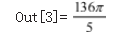SCI论文(www.lunwensci.com)
摘 要:Mathematica 数学软件具有强大的图形绘制处理和数值计算功能, 也是一个很好的辅助教学平台。本文主要结 合数学分析课程教学过程中的一些常见问题,由例题的形式,首先借助 Mathematica 软件的绘图功能进行分析和认识空间图 形,为此辅助理解三重积分的计算方法及逻辑推导计算过程 ;其次根据 Mathematica 软件的数值计算功能,验证例题的结果 及更深入理解三重积分的计算。事实证明,利用该软件辅助教学有利于激发学生的学习积极性,加深学生对相关概念及其计算 的理解,能够提升学生的数学逻辑思维能力。
Visualization of Triple Integral Based on Mathematica Software Exploration of Teaching Application
LIANG Zhipeng, YANG Jinxia
(School of Information Engineering, Tarim University, Alar Xinjiang 843300)
【Abstract】:Mathematica mathematics software has powerful functions of drawing, processing and numerical calculation, and is also a good auxiliary teaching platform. This paper mainly combines some common problems in the teaching process of mathematical analysis course, first analyzes and understands spatial graphics with the help of the drawing function of Mathematica software in the form of examples, so as to help understand the calculation method of triple integral and the logical derivation calculation process; Secondly, according to the numerical calculation function of Mathematica software, verify the results of the example and understand the calculation of triple integral more deeply. Facts have proved that using this software to assist teaching is conducive to stimulating students' learning enthusiasm, deepening students' understanding of relevant concepts and calculations, and improving students' mathematical logic thinking ability.
【Key words】:triple integral;mathematical software;Mathematica;visualization;teaching application
0 引言
数学分析课程是我校本科应用统计学和数学与应用 数学专业必修的学科基础平台课程,是初等数学通向高 等数学的桥梁,也是专业的“老三基”课程之一。作为 基础学科中的基础课程,它有其固有的特点,尤其是在 重积分教学过程中存在着大量复杂的计算和繁琐的公式 推导,使得部分学生在上课时感到非常枯燥,从而失去学习的兴趣。同时,部分学生对数学的抽象性感到十分 困惑,比如在计算重积分时,部分同学对于确定积分上 下限存在困惑,也对于一些积分区域比较模糊,从而导 致积分计算出错。另外,传统的教学过程中,主要以逻 辑推导和计算为主,显得枯燥无味,使得学生上课注意 力不集中就会跟不上教师的授课思路,从而导致学生的 学习积极性受挫。
为了提高学生的学习兴趣和学生运用数学知识解 决实际问题的能力, 把 Mathematica 数学软件融入课 堂之中不仅十分必要,而且它也是一个很好的辅助教 学平台 [1-3]。本文通过在数学分析课程教学过程中运用 Mathematica 数学软件发现,其枯燥的内容更具形象 化、具体化、生动化,其空间图形的展示更直观,具体 的演示和计算一些复杂和繁琐的问题更简化容易得到结 果,以此激发学生的学习兴趣,提高课堂教学效率。再 者, 教师利用 Mathematica 数学软件辅助教学或科研 都十分有意义,教学科研相辅相成、相互促进,以此提 升学生学习数学的内在动力。
1 利用 Mathematica 作图
在重积分计算教学过程中,对教师而言用手工绘制 二元函数的图形或是空间有界闭区域呈现出来的效果不 直观、且立体效果不佳,也浪费了有限的教学时间,对 空间感不强的学生而言稍微复杂空间立体图形的绘制更 是一件难以实现的任务,因此首要的绘图成为教与学的 困难瓶颈。Mathematica 数学软件具有强大的图形绘 制及处理功能,可以将抽象的、难以理解的空间图形形 象地展示出来,直观性显而易见。因此, Mathematica 不失为学习数学分析课程的一款有效工具。以下利用 Mathematica 作图进行实例分析,让学生有效地、直 观地突破这一瓶颈。
例 1 :空间图形 Ω 是由x2+y2+(z-2)2 ≥ 4. x2+y2+(z-1)2 ≤ 9 及 z ≥ 0 所围成的,利用 Mathematica 软件作出图形。
解 :在 Mathematica 的工作窗口输入以下命令 :
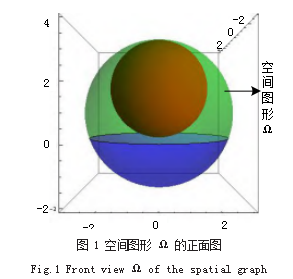
In[1]:=Show[ContourPlot3D[x^2+y^2+(z-2)^2== 4.{x,-2.2},{y,-2.2},{z,0.4},ContourStyle → {Red,Opacit y[1]},MeshStyle → None],ContourPlot3D[x^2+y^2+(z-1)^2==9.{x,-3.3},{y,-3.3}, {z,0.4},ContourStyle → {Green,Opacity[0.4]},MeshStyle → None],ContourPlot3D[x^2+y^2+(z-1)^2==9.{x,-3.3},{y,-3.3}, {z,-2.0},ContourStyle → {Blue,Opacity [0.5]},MeshStyle → None], PlotRange → {-2.4},Axes → True,Boxed → True]Out[1]= 如图 1 所示。
分析 :图 1 中的空间图形 Ω 是由大球 Ω1 除去小球 Ω2.再除去大球 Ω1 在 xoy 坐标面以下的 Ω3 所围成的, 即所示绿色部分就是空间图形 Ω。
2 三重积分的计算
教学过程中,三重积分的计算具有抽象性与复杂 性, 基于 Mathematica 数学软件的可视化方法及其数
值计算功能应用于三重积分课堂教学中,增加了教学的 直观性,并在实际教学过程中该教学方法是可行有效 的。以下先介绍三重积分的计算方法,再结合例题讲 解,为下一部分验证结果前后呼应,也可辅助理解数学 的逻辑推导计算过程。
2.1 计算方法
三重积分的计算根据坐标系不同,可分为 3 种情 形 :直角坐标系(投影法、截面法)、柱面坐标系、球 面坐标系。
2.1.1 直角坐标系
(1)投影法(“先一后二”)或(先积线,后积面)
例如,将空间有界闭区域投影在 xoy 面上,其投影 区域记为 Dxy
1)先对 z 积分(先积线)
过 Dxy 内任一点 (x,y) 作平行于 z 轴的直线,沿着 z 轴正向穿过 Ω,观察直线从曲面 z=z1(x,y) 穿入(入口 面),从曲面 z=z2(x,y) 穿出(出口面),则 z=z1(x,y) ≤ z
2.1.2 柱面坐标系
直角坐标点 (x,y,z) 与柱面坐标点 (ρ,θ,z) 之间的关系 :
分析 :计算这道三重积分的关键其实就是如何确定 积分的上下限及明确积分区域。由例 1 作出的空间图形 直观可知,空间积分区域 Ω 是由大球内部、小球外部 及大球在 xoy 坐标平面的上方所围成的。所以,在 Ω 上 的三重积分的计算可以理解为,在大球内 Ω1 上的三重 积分减去小球内 Ω2 上的三重积分,再减去大球在 xoy 坐标面以下的 Ω3 上的三重积分。确定积分的上下限利 用穿线法和穿面法,原则是入口线及入口面、出口线及 出口面对应的函数即为下限和上限。其三重积分最终的结果为
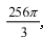
具体计算过程略。
3 利用 Mathematica 验证三重积分
Mathematica 软件除了第二部分应用的强大绘图 功能外,还有强大的计算功能,利用 Mathematica 软 件可以很容易求出上述例题中三重积分的结果,这样也 便于学生验证自己做的正确性。因此,根据上述逻辑推 导过程,分以下四步完成 :
第一步 :在 Mathematica 的工作窗口输入以下命令, 可得大球内 Ω1 上的三重积分 ;
In[1]:=Integrate[(x^2+y^2)Boole[x^2+y^2+(z-1)^2<=9],{x,-Infinity,Infinity},{y,-Infinity,Infinity}, {z,-Infinity,Infinity}]
第二步 :在 Mathematica 的工作窗口输入以下命 令,可得小球内 Ω2 上的三重积分 ;
In[2]:=Integrate[(x^2+y^2)Boole[x^2+y^2+(z- 2)^2<=4],{x,-Infinity,Infinity},{y,-Infinity,Infinity}, {z,-Infinity,Infinity}]
第三步 :在 Mathematica 的工作窗口输入以下命 令,可得大球在 xoy 坐标面以下的 Ω3 上的三重积分 ;
In[3]:=Integrate[(x^2+y^2)Boole[x^2+y^2+(z- 1)^2<=9&&z<=0],{x,-Infinity,Infinity},{y,-Infinity, Infinity},{z,-Infinity,Infinity}]
第四步 :在 Mathematica 的工作窗口输入以下命 令,可得最终结果。
4 结语
为了优化传统教学过程中枯燥无味、学生上课注意力 不集中等问题, 也为了提高学生的学习兴趣和学生运用数 学知识解决实际问题的能力,本文基于 Mathematica 软 件平台,应用探索如何实现三重积分的教与学过程。事 实证明,利用现代化教学手段既能体现出 Mathematica 软件的绘图和数值计算功能的可视化过程,也可辅助学 生认识空间图形、理解三重积分的计算方法及逻辑推导 计算过程,又验证了例题的结果及更深入理解三重积分 的计算,以此激发学生的学习积极性,提升学生的数学 逻辑思维能力。
参考文献
[1] 周保平,晁增福.高等数学实验[M].北京:北京邮电大学出版 社,2016.
[2] 干国胜,孙旭东.Mathematica在二重积分计算教与学的研 究[J].汉江师范学院学报,2018.38(6):20-24.
[3] 周小燕,杨惠,赵春艳,等.高等数学课程与Mathematica软 件相结合的教学研究[J].甘肃科技,2022.38(5):81-84.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/61897.html



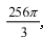 具体计算过程略。
具体计算过程略。