SCI论文(www.lunwensci.com):
摘要:随着互联网金融不断发展,金融数据的规模越来越大,其中蕴含的信息也越来越丰富。金融行为中欺诈、违规行为危害巨大,通过对金融数据的异常检测和根因分析有利于检测欺诈和违规行为,有效把控金融风险。针对大规模金融数据的异常检测与根因分析,本文提出了一套具有泛化性的面向不同类型特征因素的自动化处理框架。其中基于长短期神经网络以及周期混合学生化偏差测试的预测差值检验模型能够针对于连续值因素进行预测和检验,并在检测到异常后进行连续值因素相关性分析。这样的检测方式在高波动的序列区间具有较高召回率,在低波动区域有较高准确率。谱聚类结合模型能够将大规模离散值因子中的空间联系与时间上的偏差特征融合,在异常发生时进行快速聚类,具有灵活、高普适性以及高效的特点。
关键词:交易数据;异常检测;根因分析;聚类;无监督学习
Anomaly Detection and Root Cause Analysis for Financial Data
LI Xingang,CHEN Zhihao,YANG Yining
(UnionPay Business Co.,Ltd.,Shanghai 201203)
【Abstract】:With the continuous development of Internetfinance,the scale offinancial data is getting bigger and bigger,and the information contained in it is getting richer and richer.Fraud and irregularities infinancial behaviors are extremely harmful.Through abnormal detection and root cause analysis offinancial data,it is helpful to detect fraud and irregularities and effectively controlfinancial risks.Aiming at the anomaly detection and root cause analysis of large-scale financial data,this paper proposes a generalized automatic processing framework for different types of characteristic factors.Among them,the prediction difference test model based on long-term and short-term neural networks and periodic mixed studentized deviation test can predict and test continuous value factors,and perform correlation analysis of continuous value factors after abnormalities are detected.This detection method has a higher recall rate in the sequence interval with highfluctuations,and a higher accuracy rate in the lowfluctuation area.The combined model of spectral clustering can fuse the spatial connection in the large-scale discrete value factor with the time deviation feature,and perform rapid clustering when anomalies occur.It has the characteristics offlexibility,high universality and high efficiency.
【Key words】:transaction data;anomaly detection;root cause analysis;clustering;unsupervised learning
0引言
随着互联网和移动支付的广泛普及,大数据处理在金融行业中已经成为了一个不可避免的问题。大数据金融需要更加精准、可靠以及快速地识别和预防金融欺诈的发生,从而有效控制金融风险。银联商务作为国内最大的收单机构,服务于近800万的商户,进行海量收单数据依赖型管理是一个从粗放型经验化管理向精细化转变的一个重要途径,本文着眼于银联商务收单数据进行异常检测以及异常根因定位方面的研究,通过整理归纳分析结果以期掌握隐含规律并进行针对性的风险管理。
在很多的应用场景中,检测小规模异常样本有着广泛的需求与前景[1]。通常情况下,这些异常样本在整个数据集之中只占很小的部分且没有相对一致的特征,这给异常检测带来了诸多困难与挑战[2]。另一方面,引起异常的原因纷繁复杂,在收单中有多样的影响因子来源。针对于收单交易这样有较高安全性要求的场景,对于银联商务来说,多维度多类型因素的异常检测和根因分析是一个值得研究的问题。
1算法介绍
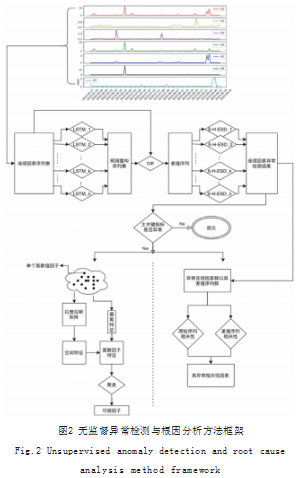
异常检测与根因分析的过程如图1所示,先对关键指标的异常进行检测,再对出现的异动进行根因分析,由无监督学习的方式进行根因分析,确定一系列可疑根因(包括连续值因素与离散因子)并交由业务人员进行解决。
本文提出的无监督异常检测与根因分析方法框架如图2所示。该框架针对连续因素与离散因子的不同特征,分别提出了长短期预测(LSTM)[3]差值检测模型与混合谱聚类[4]模型。长短期预测差值检测模型能够对于连续值序列由循环神经网络产生预测值,并通过与原始序列进行重构差值序列,对于差值序列进行学生化偏差检测(S-H-ESD)[5]。在主关键指标产生异常报告的情况下,异动根因分析将被启动。图左下部分展示了针对于离散因子的混合谱聚类模型,其结合了因子间的空间特征与当前时间点的偏差特征。图右下部分展示了针对于连续值因素集的相关性分析。
通过对于连续值因素序列的训练,特定的LSTM预测器将根据该连续值因素的特点进行学习适应,从而具备对于该连续值因素的预测能力。对于差值序列的异常检测相较于对原始序列直接进行异常检测加强了检测效果与准确度,去除了一些由于常规波动带来的影响。同时差值序列有较合理的中心分布状态。在连续值异常检测中,对于检验统计量G值的计算利用中位数代替平均值以及利用中位偏差代替方差,能够有效减少某些异常值对衡量整体平均状体以及方差状态的极端影响。连续值因素的空间相关性分析主要依靠回溯近期一段时间内的原始序列以及差值序列,分析因素之间的序列相关性。
对于离散值因素来说,模型更细化地将各个离散值因素中的离散值因子剥离出来放到同构关系图中进行考虑。通过因子间的关系添加边,再利用拉普拉斯矩阵提取空间特征向量。此外通过频率构建的时间特征也将被结合构建时空特征。利用时空特征对于大规模离散值因子进行无监督聚类,能够确定一定范围的异常的离散值因子。这样的操作方法能够处理较大规模的离散值因子,较快地对于可疑离散因子进行聚类。
通过提出对于连续因素以及离散值因子的异常检测与根因分析方法,模型能够处理绝大多数金融交易场景中的数据异常问题,并且具有较好的泛化性。
2实验结果与分析
2.1连续值因素预测差值检测模型(Preditector)
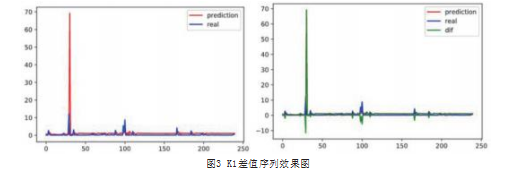
以某个因素序列K1(交易金额)为例,预测值与真实数据产生的差值序列能够有效地捕捉乃至放大原始真实序列的异常波动,如图3所示,将这样异常放大后的序列进行S-H_ESD异常检测,能够有更高的识别准确性以及召回率。
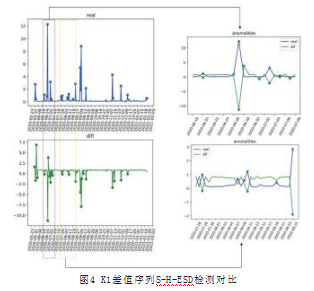
图4为用差值序列进行异常检测的结果,与直接对原始序列进行异常检测的结果进行比较。图4红框剧烈波动的区域(右上放大图所示)中,差值序列的S-H-ESD检测结果相较于原始序列直接进行检测的结果表现了更高的召回率,在短时间内召回的异常点数要高40%。而对于低波动范围的黄框区域(右下放大图所示),差值序列的S-H-ESD检测结果具有更高的准确率。实验结果显示,对原始序列进行S-H-ESD检测更加倾向于检验出峰值,而差值序列更能够在剧烈变化的过程中检验出异常。对于原始序列进行S-H-ESD检验得出的异常点来说,差值序列的结果能够大范围覆盖,并且在一些剧烈波动处的异常密度更高。例如对于6月22日至7月4日范围内的剧烈波动,差值序列的检测结果具有更高的敏感度;而在8月初的小幅波动时,差值序列的检测结果具有更高的准确度。从这点上来看,利用预测器得到的差值序列进行S-H-ESD检测得到的异常结果更加具有根据波动情况动态调整的能力,也说明预测差值检测模型的有效性。
2.2连续值因素根因分析
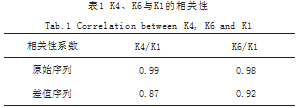
本文以K1-K7七个连续序列因素为例,时间跨度为自2019年6月8日开始的230天,对每个序列做LSTM预测器处理之后,得到七个在测试时间内的差异序列,如图5所示,其中每一幅子图对应了一个因素。分析异常需要先排除那些没有在该时段有异常表现的序列。对于6月24日至7月4日这段时间的突变异常来说,K1,K4和K6均检测出了异常,我们可以初步判断K4与K6有可能与K1的异常有关,而无需再考虑K2,K3,K5和K7等等因素。对于异常发生的节点判断根因,需要查看这三个异常序列的相关性。例如在7月4日这个节点向前半个月的时间窗内,三个因素原始序列的相关性与差异序列的相关性将会作为根因判断的重要依据,相关性结果如表1所示。
对于这些相关性系数,可以判断K4与K6对于K1在这段时间的异动呈高度相关。如图6将这段时间内三个因素放大,经过分析发现,三者的整体走势都很相近,而对于6月24日至次月4日的异常来说,三者成同样的走势。因此可以确认K4与K6均为K1关键指标的相关根因。
值得注意的是,K3这一因素,如图7所示,在异常窗口6月24日之前发生了异动。而这里的异常取窗(在6月24日之后)会忽略之前的异常的影响,也就是通常情况下忽略含有较大延迟的潜在弱根因相关性。如果需要关注这种含有较大时间延迟的弱根因相关性,可以在调整异常检测取窗的基础上使用含延迟时间系数的相关性分析。
在图7中,分别对K1和K3两个序列进行向前滑窗(起始位置为诊断出K1异常的6月24日-29日)的相关性比较,图7的热力图中的横坐标代表在K3上的滑动,而纵坐标代表在K1上的滑动。在当下位置,也就是起始位置,可以关注热力图的最后一行来判断(在K1滑动为零的时候)是否有一些之前的K3序列与当前的K1异常高度相关。24-28日K1与七日前17-21日K3的相关性进行了计算,得到了较高的相关性系数。需要注意的是,相同时间17-23日K1与17-21日K3的相关性系数,如热力图中(-7,-7)位置所示。事实上K3在18日左右的异常是与K1的18日时的异常相结合的,而并不是K1在所观察24-28日时间窗异动的原因。在热力图中,靠近对角线的高相关性相较于远离对角线的高相关性更强,因为越靠近对角线表明时间延迟系数越小,表明这样的相关性更加敏捷。此外如果想要进一步对根因的因果性进行分析,还可以进一步对时间颗粒度进行调整。例如将模型精确调小时,然后对新的细粒度预测器得到的差异序列进行异常检测,判断出现异常的先后顺序。这样的异常先后顺序从某种程度上体现了一定的根因的因果关系。
2.3离散值根因分析
对于离散值因子来说,本文使用用户、商品、地址、用户来源和种类五个因素,其中用户有2500个(在订单中实际出现1746个)、商品200件,地址48个州,5个用户来源以及4个商品种类。这里用户、地址以及用户来源之间有着相互关系,商品以及商品种类也有着关系。这些关系都体现在了一张由两千七百多个节点组成的图谱之中。节点1-2500为用户节点,2501-2700为商品节点,以此类推。这张图的对角线度矩阵与邻接矩阵的差值就构成了一个描述这个图的拉普拉斯矩阵。通过拉普拉斯矩阵的特征空间向量,可以得到如图8中四个小图所示的结果。在横坐标中,1-2500为用户因子,这些同类因子在四个维度的空间特征都较为类似,说明同类因子在不同的特征向量中具有类似的特征。此外可以发现不同的特征向量提取的空间关系也不尽相同。在上两幅的图中,用户因子的区分度较低(1-2500用户因子的特征值均趋于0),而在下两幅图中,用户因子内的区分度较大(1-2500用户因子的特征值的分布扩张到-0.5与0.5之间)。对于商品因子(2501-2700)来说,在上两幅的图中区分度较高,而在下两幅图中较低。因本文将这种现象概括为不同的特征向量能够提取不同潜在的空间特征信息。
图9为5个离散值因子空间特征聚类结果,这样的聚类方式能够比较好地提取到因素之间的空间信息,通过潜在的空间特征信息起到分离不同类因素的效果。在处理含有关系的离散值因子的问题时,通过关系图谱类的方式能够达到广泛的区分因素层次的作用。也就是说,空间特征对于离散值因子节点之间的关系的描述是较为准确的。
无监督聚类的精度与种类数目呈正比,也就是说设置越多的聚类中心,能够让可疑异常因子群的准确度更高。但是与此同时,由于离散因子的稀疏性,它们的频率序列会呈现较高的二值化程度,这样的分布状况导致在追求高准确率时会出现天然的召回率下降的问题。因此在选取聚类类数时,需要结合目标精度与偏离特征分布状态进行调整。
3总结
本文基于金融大数据的自动化分析,提出异常检测与根因分析解决方案。该方案主要分为两个方面,一是对连续值因素的差值检测模型,另一个为处理离散值因子的谱聚类模型。连续值因素的差值检测模型结合了LSTM预测模型与S-H-ESD异常检验方法,通过对连续值因素序列的训练,特定的LSTM预测器将根据该连续值因素的特点进行学习适应,从而具备对该连续值因素的预测能力。对于离散值因素,本文细化地将各个离散值因素中的离散值因子剥离出来放到同构关系图中,它能够取因子间的关系构造节点的若干空间特征维度。此外还将描述异常频率偏离程度的偏差特征维度与空间特征维度拼接构成一个包含时空信息的多维特征。利用这样的时空特征对于大规模离散值因子进行无监督聚类,能够确定一定范围的异常的离散值因子。通过提出对连续因素以及离散值因子的异常检测与根因分析方法,模型能够处理绝大多数金融交易场景中的数据异常问题,并且具有较好的泛化性。
参考文献
[1]Grubbs,F.E.,Procedures for detecting outlying observations in samples[J].Technometrics,1969,11(1):1-21.
[2]Goldstein,M.and S.Uchida,A comparative evaluation of unsupervised anomaly detection algorithms for multivariate data[J].PloS one,2016,11(4):p.e0152173.
[3]Hochreiter,S.and J.Schmidhuber,Long short-term memory[J].Neural computation,1997,9(8):1735-1780.
[4]Chen W Y,Song Y,Bai H,et al.Large-Scale Spectral Clustering with Map Reduce and MPI[J].Scaling up Machine Learning:Parallel and Distributed Approaches,2011,1(1):240-261.
[5]Hochenbaum J,Vallis O S,Kejariwal A.Automatic Anomaly Detection in the Cloud Via Statistical Learning[J].2017.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/37579.html