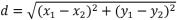SCI论文(www.lunwensci.com):
摘 要:K-means 聚类算法是一种以距离为依据进行聚类的算法,原理简单且便于处理数据,但对于呈环形分布的数据集,传统的 K-means 算法的聚合结果并不理想。因此,本文提出了基于环形数据集的改进 K-means 聚类算法,引进了原 点相对距离差的概念,将欧氏距离的计算改进为原点相对距离差的计算,使得数据集聚类为环形状。实验结果表明,改进的 K-means 聚类算法处理呈环形分布的数据集效果更好。
关键词:K-means 聚类算法 ;环形分布数据集 ;原点相对距离差
Improved K-means Clustering Algorithm Based on Circular Data Set
ZENG Yimiao
(School of Mathematics and Computational Science, Hunan University of Science and Technology, Xiangtan Hunan411100)
【Abstract】: K-means clustering algorithm is a clustering algorithm based on distance. Its principle is simple and easy to process data. However, for data sets with ring distribution, the aggregation result of traditional K-means algorithm is not ideal. Therefore, this paper proposes an improved K-means clustering algorithm based on ring data set, and introduces the concept of relative distance difference of origin. The calculation of Euclidean distance is improved to the calculation of relative distance difference of origin, so that the data set is clustered into ring shape. The experimental results show that the improved K-means clustering algorithm is better in dealing with data sets with circular distribution.
【Key words】: K-means clustering algorithm;circular distribution data set;relative distance difference of origin
0 引言
随着社会进入大数据时代,对大量数据的处理与分 析是非常重要的。利用数据挖掘能够从数据中抽取出隐 藏的有用信息,从而广泛应用于物流领域、商务智能等 各行各业 [1-5]。在数据挖掘技术中,聚类分析是非监督 的机器学习算法,其模型可以建立在无类标记构成的训 练数据上。聚类算法以距离或相似度为依据进行划分, 使得组内距离最小,而组间距离最大。
K-means 聚类算法,也称为快速聚类法,是其中一种利用均值的计算对数据进行聚类的算法,原理简单且便于处理数据。然而,传统的 K-means 算法存在一些缺陷导致聚类效果不理想。因此,产生了多种对传统的 K-means 算法的改进方法,对初始聚类中心的选择进行了改进 [6-7],优化了 k 值和初始聚类中心 [8-9],提出了对迭代过程的改进 [10]。本文针对呈环形分布的数据 集,提出了改进的 K-means 算法,将欧氏距离的计算 改进为原点相对距离差的计算。实验结果表明,基于环 形数据集的改进 K-means 聚类算法在聚类上效果较好。
1 相关定义和概念
为了便于表述和理解,本文给出以下定义及概念 :
欧式距离 :在平面直角坐标系中,设两点 a=(x1,y1), b=(x2,y2),则两点之间的距离为
原点相对距离差 :在平面直角坐标系中,设两点 a=(x1,y1),b=(x2,y2),则称两点分别到坐标原点的距离 的差的绝对值为原点相对距离差,表示为

聚类中心 :设归属于同一个聚类中心的数据集 typei={ci1,ci2,… ,cin},其中 cij=(xij,yij),i=1,2,… ,k,j=1,2,… ,n, 则更新后的聚类中心 μi 表示为
 2 传统的 K-means 聚类算法
2 传统的 K-means 聚类算法
传统的 K-means 算法是通过不断迭代求解的聚类 算法,根据距离函数将数据分为 k 类。以距离作为相似 度的依据,距离越小的两个点,则相似度越大。因此, 每一类的点相似度较大,而类与类间相似度较小,最终得到 k 类独立的簇。传统的 K-means 聚类算法 [11] 的 一般步骤如下 :
(1)选择 k 值和初始聚类中心。k 值和聚类中心的 选择会影响聚类效果。
(2)通过计算各点和各聚类中心的欧氏距离,将样 本点分配到欧氏距离最小的聚类中心集合中,归为一类。
(3)更新聚类中心。对每一类聚类中心集合,重新 计算聚类中心,从而获得新的聚类中心。
(4)不断迭代,反复执行第二、三步,直至满足一 定的条件,终止循环,得到最后的聚类结果。
3 改进的 K-means 聚类算法
对于呈环形分布的数据集,本文提出了改进的 K-means 算法,将欧氏距离的计算改进为原点相对距离差的计算, 从而得到环形状的聚类。具体步骤如下 :
3.1 构造环形分布数据
本文利用极坐标产生呈环形分布的数据集 C={c1, c2,… ,cm},并转化至直角坐标系,其中一个数据集可视 化后如图 1 所示。
3.2 随机选择 k 个聚类中心
通过观察可视化后的数据样本点,确定聚类中心的 数量 k,并随机产生 k 个聚类中心,分别为 μ1,μ2,… ,μk, 对应于每个聚类中心的集合分别为 type1,type2,…,typek。
3.3 改进算法――计算原点相对距离差
对于呈环形分布的数据,欧氏距离在该条件下不再 适用,本文提出了原点相对距离差的定义,即计算样本 点和聚类中心分别到原点距离的差值。由公式 (2),比 较样本点和每个聚类中心的原点相对距离差,若某个样 本点 cj 与某个中心点 μi 的原点相对距离差最小,则把 该样本点归到集合 typei 中。
3.4 更新聚类中心
数据样本点每次归类后,计算每一类聚类中心的数据 集,得到新的聚类中心。因此,第 i 类聚类中心的数据 集为 typei={ci1,ci2,… ,cin},其中 cij=(xij,yij),i=1,2,… ,k, j=1,2,… ,n,由公式 (3) 更新所有聚类中心。
3.5 迭代至条件终止
通过不断对数据样本点归类并更新聚类中心,当各 个样本与所在类均值的误差平方和小于某一定值时,即 满足终止条件,迭代结束得到最后的聚类结果。
4 实验结果分析
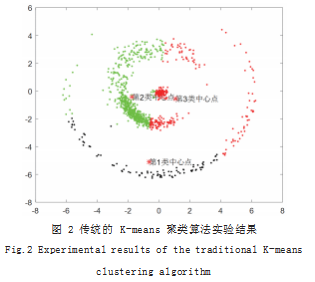
4.1 传统的 K-means 聚类算法实验结果分析
对于本文的具有环形分布特征的数据集,本文采用 传统的 K-means 聚类算法进行测试,实验结果如图 2 所示。由图像可得,聚类效果明显较差,这是因为传统 的 K-means 聚类算法以欧式距离作为聚类依据,每次 迭代时将与聚类中心的欧氏距离最小的样本点归类在一 起,忽略了数据集的总体特征。因此,对于呈环形分布 的数据集,传统的 K-means 聚类算法不再适用。
4.2 改进的 K-means 算法实验结果分析
在实验过程中,本文构造了具有环形分布特征的数 据集。与传统的 K-means 聚类算法不同的是,针对环 形特征的数据,本文引进了原点相对距离差的定义,在 聚类迭代过程中,通过计算样本点到聚类中心的原点相对距离差进行样本点的划分。通过数据可视化,本文得 到如图 3 ~图 6 所示的实验结果。每次实验的数据都被 很好地归类,聚类结果较好,表明改进的 K-means 算 法是有效的,每一种聚类是合理的。
5 结语
为了更好地对呈环形分布特点的数据集进行聚类分 析,本文提出了改进的 K-means 聚类算法,将欧氏距 离的计算改进为原点相对距离差的计算。(1)通过数据 可视化后随机选择 k 个聚类中心 ;(2)计算样本点和聚 类中心分别到原点距离的差值,将差值小的样本点归至 该聚类中心的集合中 ;(3)更新聚类中心点 ;(4)直至 满足各个样本与所在类均值的误差平方和达到最小,结 束迭代。实验结果表明,相比传统的 K-means 算法, 改进的 K-means 算法更适用于呈环形分布的数据集的 聚类,效果更好。
参考文献
[1] 王勇,黄思奇,刘永,等.基于K-means聚类方法的物流多配送 中心选址优化研究[J].公路交通科技,2020,37(1):141-148.
[2] 蔺小清.大数据时代K-means聚类算法应用于在线学习行为研究[J].电子设计工程,2021,29(18):181-184+193.
[3] 张萌谡,刘春天,李希今,等.基于K-means聚类算法的绩效 考核模糊综合评价系统设计[J].吉林大学学报(工学版),2021,51 (5):1851-1856.
[4] 杨真真,方秀男.基于K-means++聚类算法的各省市生产总 值增长水平聚类分析[J].中国科技信息,2021(17):98-99.
[5] 钟穗希,李子波,唐荣年.基于PCA-Kmeans聚类法的橡胶树 叶片氮含量的近红外高光谱诊断模型研究[J].海南大学学报(自 然科学版),2020,38(3):260-269.
[6] 王美琪,李建.一种改进K-means聚类的近邻传播最大最小 距离算法[J].计算机应用与软件,2021,38(7):240-245.
[7] 张嘉龙.一种新的选取K-means初始聚类中心算法[J].现代 计算机,2021(18):56-59.
[8] 马钰,莫路锋.通过密度思想和聚类有效性指标改进的K- means算法[J].现代电子技术,2021,44(17):120-123.
[9] 王巧玲,乔非,蒋友好.基于聚合距离参数的改进K-means算法[J].计算机应用,2019,39(9):2586-2590.
[10] 宋国兴,张清伟,郑明钊,等.基于Spark Streaming的并行 K-means改进算法研究[J].现代计算机,2021(18):68-71.
[11] 丛思安,王星星.K-means算法研究综述[J].电子技术与软 件工程,2018(17):155-156.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jisuanjilunwen/35651.html