SCI论文(www.lunwensci.com):
摘要:随着现代信息技术的发展,运用几何画板轨迹功能解决数学问题,能够将复杂的问题形象化、简单化,从而激发学生的学习兴趣。
关键词:几何画板;轨迹;动态
本文引用格式:王露.例谈几何画板轨迹功能求解初中数学问题[J].教育现代化,2019,6(31):170-171+183.
几何画板是数形结合的强有力的工具,能够将枯燥、复杂的数学问题用直观的“形”表示出来,几何中的运动轨迹问题以及图形拼接涉及运动、轨迹等较为抽象的概念,知识点多、覆盖面广、运算量大,是教学中较为棘手的问题,几何画板具有“运动变化过程中保持几何关系不变”的特点,在动态演示中,观察轨迹的形状,思考形成的原因,诱发解题思路,激起学生探究欲望,破解求动点轨迹的难题,并为问题进一步拓展创造了条件[1]。
一几何图形中的运动轨迹问题
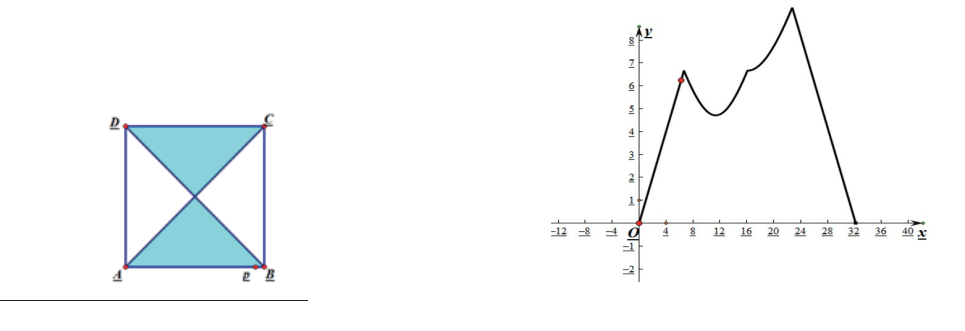
例题:如图所示,动点P沿着A→B→D→C→A的方向移动,求P在移动过程中路程的变化情况,以及点P到点A之间距离的变化情况。问题的分析:此类问题的动态性、抽象性是教师讲授的难点,也是学生吸收的重灾区,光凭教师的讲述很难使学生在头脑中建构出准确的数学模型,几何画板则能够将动点距离初始点的长度的变化情况用图像表示出来,使学生理解得更加透彻,有利于学生对知识点的吸收和掌握。具体绘图步骤如下:
(1)打开几何画板,用线段直尺工具画出一条线段,再单击变换窗口中的旋转,构造出一个正方形ABCD。
(2)点击多边形工具,在正方形ABCD内部沿着A→B→D→C→A的方向移动构造多边形,如图所示:
(3)选中线段AB,度量出AB的长度为4.95厘米,并计算所构造的多边形的周长为23.89厘米。
(4)选择线段直尺工具,画线段EG,在线段EG
上任取一点F,度量点F在线段EG上的值为0.21。
(5)选中构造的多边形,打开”绘图→在四边形上绘制点”命令,将值设为点F在线段EG上的值,点击确定,得到点P。
(6)依次选中点F,点P,选择”变换→创建自定义变换命令”,创建关于F→P的变换。
(7)依次选中线段EF和点P,选择“F→P变换”命令,创建关于线段EF→P的变换。
(8)连接点A和点P,度量线段AP的值,并计算所构造多边形的周长和点F在线段EG上的值的乘积为M。
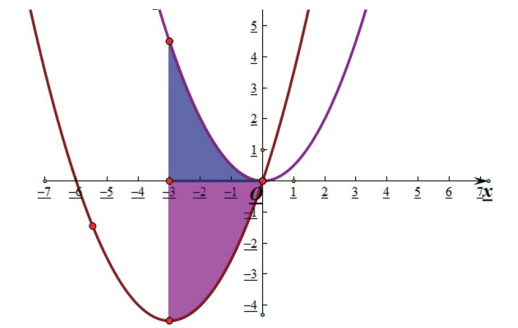
(9)点击自定义工具,选择迷你坐标系,建立坐标系,在坐标系上绘制以M的值为横坐标,以线段AP长度为纵坐标的点Q。
依次选中点F和点Q,选择“构造→轨迹”命令,此时便绘制出了点P运动的轨迹,横坐标表示点P运动的路程,纵坐标表示点P到点A之间的距离。
二 不规则图形的拼接问题
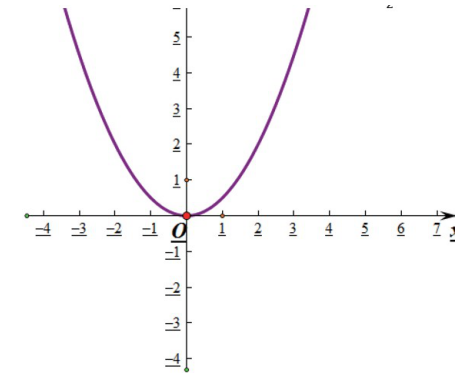
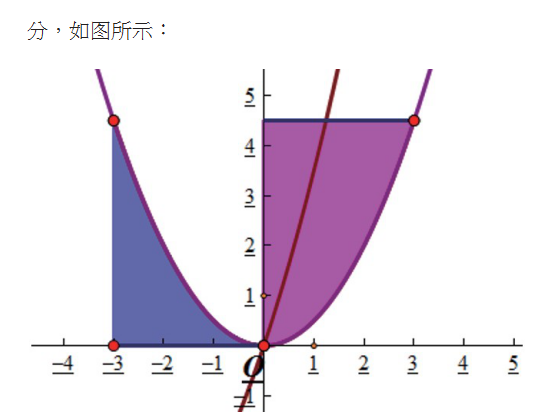
例题:如图,把抛物平移得到抛物线M,抛物线M经过点A(-6.0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线交于点Q,则图中阴影部分的面积为()
分析:此题图形属于不规则图形,对于求解这类不规则图形的面积,只能通过拼接的方式,将阴影部分拼接成一个规则的图形,几何画板的轨迹功能可以将整个拼接的过程通过动画展示出来,学生理解起来也更加简单、深刻。下面我将介绍利用几何画板解此题的具体步骤 :
(1)打开几何画板,选择“数据→新建函数”命令,新建函数。
(2)选择“自定义工具→迷你坐标系→平面直角坐标系”,并初始化直角坐标系。
(3)双击坐标系原点,选中函数式: t, 点击右键,选择绘制函数,得到二次函数图像,如图所示:
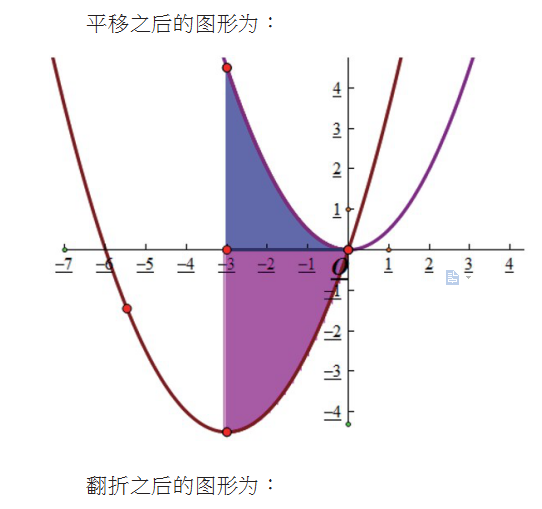
(4)由题可知平移后的图像过点P(-3,-4.5),选择“绘图→绘制点”命令,在坐标系中绘制点P。
(5)依次选中原点和点P,选择“变换→标记向量”命令。
(6)在函数图像上任意绘制一点Q,选择”变换→平移”命令,得到Q’。
(7)依次选中点Q和点Q’,选择“构造→轨迹”命令。
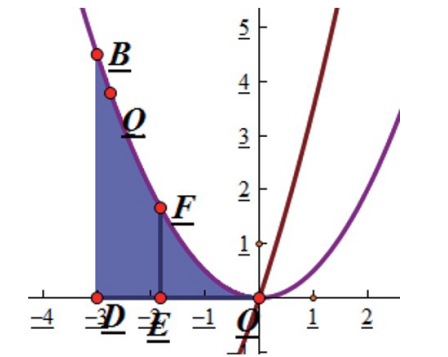
(8)依次选中点P和y轴,选择“构造→平行线”命令,得到直线J,直线J与函数图像的交点B,以及直线J与X轴的交点D。
(9)连接O,在OD上任取一点E,依次选中点E和y轴,选择“构造→平行线”命令,得到平行线与函数曲线的交点F,连接EF。
(10)依次选中点E和线段EF,选择”构造→轨迹”命令,所得图形如下:
(11)依次选中点E和点F,选择”构造→轨迹”命令,得到BO段函数曲线的轨迹,在轨迹上任取一点G,双击y轴,做镜面反射,选择“变换→反射”命令,得到点G’,连接GG’。
(12)依次选中原点O和点P,选择“变换→标记向量“命令,再选中G’,选择”变换→平移”命令,得到点G’’。
(13)选择多边形和边工具,依次过点G,点G’,点G’’构造四边形AGG’G’’,在四边形上绘制点H,再合并点A和点G’。
(14)依次选中点G和点H,构造轨迹,得到轨迹L。
(15)选择“数据→新建参数”命令,新建参数t[1]=1.00,和t[2]=0.00,选中轨迹L,选择”绘图→绘制轨迹上的点“命令,在弹出的对话框中,将值选为t[1],单击绘制按钮,再将绘制的点建立一个隐藏显示按钮,并将标签改为起点;同理绘制值为t[2]=0的点,建立隐藏显示按钮,标签为终点。
(16)依次选中起点和X轴,构造平行线K,再依次选中终点和平行线K,构造垂线I,得到垂线I与平行线K的交点M。
(17)用同第⑨和第⑩步相同的方法构造阴影部
所以不规则图形阴影部分的面积最终转化成了求矩形的面积。
三 小结
几何画板作为现代教育的辅助工具,有助于学生在一个动态的演示过程中形象直观的理解知识的发生和发展的各个环节,从而让学生很好的理解和掌握所学的知识,不仅如此,几何画板在解决各类轨迹问题,尤其是开放性的试题时,通过直观展示轨迹形成,为我们解题指明了方向,提供了新的思路[2]。
参考文献
[1]梁金兰,唐剑岚.巧用几何画板拓展解析几何动点轨迹问题[J].数学之友,2015(4):73+77.
[2]何立特.几何画板在探究轨迹问题中的应用[J].河南教育学院学报(自然科学版),2009,18(3):65-66.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/9838.html