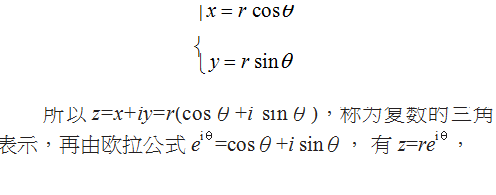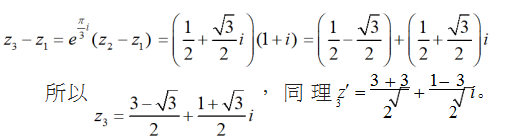SCI论文(www.lunwensci.com):
摘要:复变函数做为一门基础数学课程,在工程中应用非常广泛,是很多工科专业的专业基础课。复数作为复变函数研究的对象,它的表示方法有很多种。而不同的表示方法都有自己独特的优点。文章针对常用的几种复数表示方法探究它们各自优点并给出相应实例,以便学生深刻理解各表示方法,更好的理解复数,从而更好的掌握复变函数的理论,为后续专业课程的学习打下坚实的基础。
关键字:复数;代数表示;几何表示
本文引用格式:唐贤芳 等 . 浅谈复数的表示方法 [J]. 教育现代化,2019,6(28):168-170.
复变函数是一门基础数学课,很多工科专业都开设这门课程。它在工程中的应用非常广泛,比如物理学上有很多不同的稳定平面场,对它们的计算就是通过复变函数来解决的,再比如俄国的茹柯夫斯基在设计飞机的时候,就用复变函数论解决了飞机机翼的结构问题。而作为复变函数研究的主要对象复数,它的表示方法很多。常用的有代数表达, 几何表达。而几何表达中有点表示,向量表示,三角表示与指数表示。为什么同一个点,引进不同的表达?下面就针对不同的表示方法谈谈它们的作用和解决的问题。
一 代数表达
定义 1:对任意两实数 x,y, 称 z=x+iy 为复数, 其 i 为虚单位。我们把这个方式表达出的复数称为复数的代数表达。这种表达方式的优点是可以将复数问题实数化。比如我们通过代数形式定义出的复数加法运算,就可以归结为实部与虚部的加法,即实数的加法。有了复变函数概念后,我们有如下定理 1,2 成立。

以上定理的重要作用在于,讨论复变函数的极限,连续性等价于它所对应的二元实变函数的极限与连续性的讨论。在研究实数时,为了形象的表达数字我们建立了坐标轴,通过坐标轴上的点表示数,使得很多问题能够便于理解。同样,为了便于理解我们引入了复数的几何表示。
二 复数的几何表示
(一) 点表示
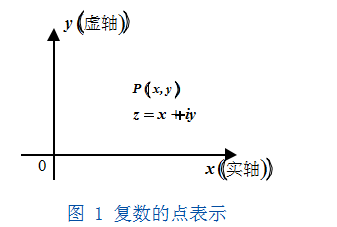
一个复数 z=x+iy 对应于一对实数 (x,y),于是在平面上建立坐标系 XOY,用坐标是 (x,y) 的点 P 表示复数 z,如图 1 所示。从而可以使我们可以借助于几何语言和方法研究复变函数问题,也为复变函数应用于实际奠定了基础。
(二) 复数的向量表示
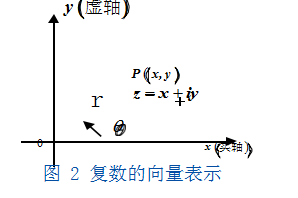
连接点 z 与坐标系圆点 O 得到向量 OP,即为复数的向量表示。如图 2 所示。
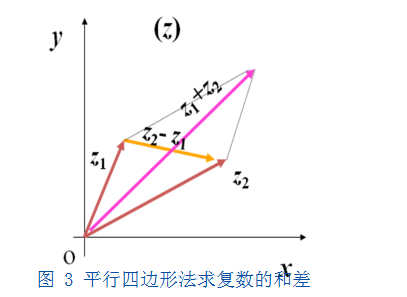
至此,我们就可以利用几何上的性质来解决复数的问题。比如在直角三角形 VOPA 中如图 2 所示, 利用三角形的直角边的长度小于斜边长度很容易理解 |x|≤|z|,|y|≤|z|,利用三角形两边和大于第三边则有 |z|≤|x|+|y| 成立。再比如有了复数的向量表示后, 复数的加法与减法运算可以利用平行四边形来理解, 如图 3 所示。

给出向量表达后,向量的长度 r 称为复数z=x+iy 的模或绝对值。以 x 轴正方向为始边 ,OP 为终的的夹角 θ 称为复数 z=x+iy 的辐角,如图 2 所示。从图形上容易得到 :
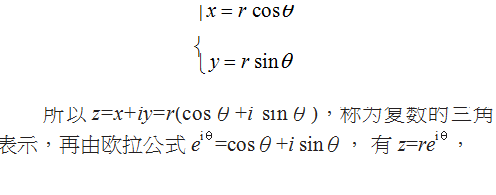
称为复数的指数表示。他们的引入在复变函数中有什么作用呢?
(三) 三角与指数表示
三角与指数表示是引入模与辐角表示复数,这种表达的优点与向量表达类似,可以用几何知识解决复数问题。利用三角表达,不难推得如下定理三成立。
定理 3:两复数相乘 , 只要把它们的模相乘 , 辐角相加。

法具有显著的几何意义,即 Z1Z2 相当于将 Z1 的模伸缩 |Z2 | 倍数,辐角增加 Argz2。这样的几何意义在解决有关几何问题时会发挥它特有的优点。如下题:
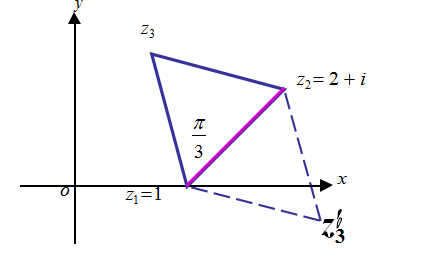
例 1: 已 知 正 三 角 形 的 两 个 顶 点 为 Z1=1 与Z2=2+i,求它的另一个顶点。
解:将已知的两点及由它们作为顶点所构成的正三角形画在直角坐标系下,如图 4 所示:

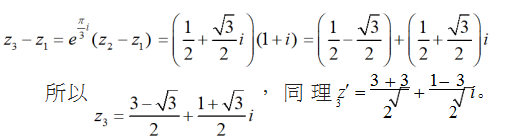
上题就是灵活运用复数的乘法的几何意义,结合正三角形的几何特点解决此问题。
三 结束语
同一个复数有几种不同的表达,引入不同的表达是因为每种表达都有它独特的优点。比如代数表达,这样的表达使得我们很多有关复数的问题能够实数化。几何表达因为它显著的几何意义,使得我们在处理很多问题时直观,简单化。深刻理解每种表达的优点,使我们能够更好的理解复数,从而更好的掌握复变函数的理论,为实际应用打下坚实的基础。
参考文献
[1]盖云英,包革军编.复变函数与积分变换[M].高等教育出版社,2008.
[2]杭俊,张燕.浅谈“化复为实”思想在“复变函数”教学中的应用[J].电气电子教育学报,2018,40(4):101-104.
[3]罗嘉锐.复变函数在通信工程中的应用分析[J].通讯世界,2017,(11):54-55.
[4]唐贤芳,张如,贾亚朝.独立学院复变函数与积分变换教学改革探讨[J].中国教育技术装备,2016:105-106.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/9393.html