SCI论文(www.lunwensci.com)
[摘要]表现性评价是通过动作、操作、写作等客观测评,对学生的口头表达能力、书面能力、思维能力、创造力和实践能力等进行评价。本文以人教版小学数学五年级上册“平行四边形的面积”课时作业的表现性任务为例,通过开发素养导向的测评工具,确定测什么和怎么测;运用素养导向的测评工具,确定测评对象并分析结果;借助大数据改进教学活动,定位教学短板和精准评价学生。
[关键词]表现性评价;平行四边形的面积;课时作业
《义务教育数学课程标准(2022年版)》(以下简称“新课标”)指出,要改变过于注重以课时为单位的教学设计,推进单元整体教学设计,体现数学知识之间的内在逻辑关系,以及学习内容与核心素养表现的关联。可见课时作业的设计要基于单元整体编排进行设计,摒弃传统的“二元对立”评价方式,借助表现性评价真实呈现学生的数学思维水平。
以人教版小学数学五年级上册第六单元“平行四边形的面积”课时作业的表现性任务为例,通过测评工具的开发、测评工具的运用和教学活动的改进等过程,构建基于素养立意的课时作业表现性评价,精准定位学生在作业中的具体表现和认知水平。
一、开发素养导向的测评工具
评价发挥着育人导向的作用,应努力实现以评促学和以评促教的功能。评价贯穿在教学和作业过程中,尤其是在课时作业的监测环节,教师要考虑以下两个问题:①测什么,即课时作业的评价目标;②怎么测,即课时作业的设计原则。让课时作业能合理地反映学生掌握知识技能的水平,承载起落实数学核心素养的功能。
(一)测什么:确定作业的评价目标
为了确定课时作业的评价目标,教师需要研读课标、教参和教材,确定课时作业的知识技能、数学思考和问题解决等方面的要求,并划分好不同水平层次的具体表现标准。基于以上的整理与思考,我们确定了“平行四边形的面积”课时作业评价目标,并对作业评价目标进行具体化(见表1)。
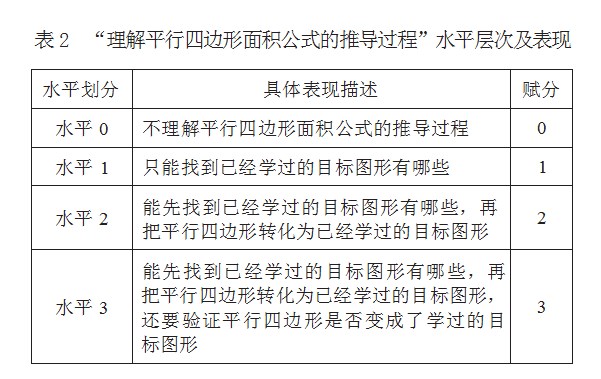
接着,我们确定了各个作业测评知识点的水平层次,方便教师合理地评价学生的具体表现。以“理解平行四边形面积计算公式的推导过程”这个作业测评知识点为例,划分出具体的表现水平(见表2)。
细化课时作业测评点过程中明确测什么,既能指导教师的教学行为,还能清晰地刻画学生在作业中的表现。
(二)怎么测:确定作业的设计原则
基于素养导向的表现性评价更加关注学生的思维过程,促进学生知识技能和关键能力的形成,在设计课时作业时应遵循思维可视化、过程开放化、情境生活化等原则。我们确定了“平行四边形的面积”课时作业的表现性任务。
测评知识点:理解平行四边形面积公式的推导过程表现性任务:
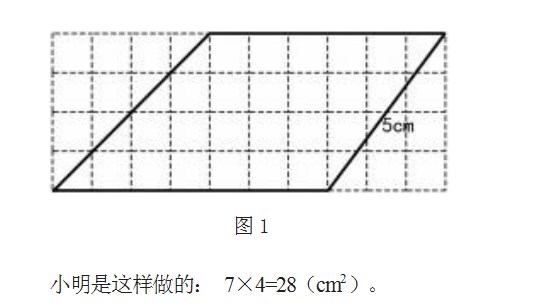
这个图形(图1)的面积是多少?(每个方格的边长是1厘米)
(1)你觉得小明是怎么想的?
(2)你同意小明的做法吗?为什么?
设计意图:以凸平行四边形为习题素材,先让学生解释错误的解答过程,再引导学生思考正确的解答过程。
测评知识点:用平行四边形的面积知识解决问题
表现性任务:
一个平行四边形草坪的一条高是4.8米。
(1)请你在图(图2)上分别填入10和6,说明你的理由。
(2)画出两种相对应的“转化后的长方形”,并标出长和宽。
(3)至少用两种方法计算面积。
设计意图:以生活中的平行四边形为习题素材,第1小题考查学生能在具体情境中确定底和高;第2小题考查学生转化前后图形的面积不变;第3小题考查学生能找到平行四边形中对应的底和高并计算面积。
测评知识点:解决“等底等高”的平行四边形面积相等的变式问题
表现性任务:
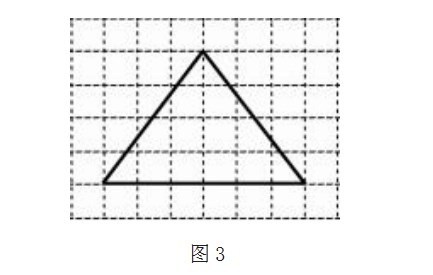
这个图形(图3)的面积是多少?用尽可能多的方法计算。(每个方格的边长是1厘米)
设计意图:此题引导学生用等底等高、割补等转化方法探究三角形面积计算方法,实现转化方法的迁移。
二、运用素养导向的测评工具
设计好表现性评价的测评工具后,教师就要经历确定测评对象和测评过程,并分析测评结果等测评活动。
(一)确定测评对象
按照现行的小学数学人教版教材,我们选择了五年级56名刚刚学习“平行四边形的面积”一课的学生进行课时作业的测评活动。
(二)测评和访谈过程
测评时间选择在2022年10月20日,为了保证测评的有效性,教师上完“平行四边形的面积”新授课后就下发课时作业,没有给予任何提示和指导。整个测评过程真实地反映了学生在独立情境下运用平行四边形面积解决问题的能力。
当学生完成“平行四边形的面积”课时作业后,教师批改了学生的作业,并对部分学生进行了访谈,有助于更加清晰地了解他们的思考过程。
(三)分析测评结果
1.对某道题的测评结果分析
以第一个表现性任务为例,测评知识点是“理解平行四边形面积公式的推导过程”,我们统计了四个层次的学生人数。
水平为0,即“不理解推导过程”的有0人。
水平为1,即“只知道目标图形”的有3人,占总人数的5.3%。具体表现如图4。
水平为2,即“知道目标图形,能把现有图形转化为目标图形”的有31人,占总人数的55.4%。学生具体表现如图5。
水平为3的,即“知道目标图形,能把现有图形转化为目标图形,还验证现有图形与目标图形面积是否相等”的有22人,占人数的39.3%。具体表现如图6。
2.对课时作业的测评结果分析
(1)近40%的学生主动验证现有图形与目标图形的关系。从表4可以看出,5.3%的学生知道要把凸平行四边形转化为长方形,但不知道如何转化。94.7%的学生能把凸平行四边形转化长方形或三角形,仅有39.3%能发现凸平行四边形不能完全转化成长方形,需要验证凸平行四边形是否变成了长方形,即凸平行四边形与长方形的面积是否保持不变。
(2)近90%的学生能找到平行四边形与长方形的对应关系。
从表3可以看出,8.9%的学生处于水平0,即学生不能解决第二个表现性任务中的3个小题;14.3%的学生处于水平1,即学生只能解决第二个表现性任务中的第1小题;23.2%的学生处于水平2,即学生能解决第二个表现性任务中的第1和第2小题;53.6%的学生处于水平3,即学生能解决第二个表现性任务中的3个小题。
(3)近80%的学生至少能用两种方法解决三角形面积。
从表4可以看出,8.9%的学生处于水平0,即学生不能解决三角形面积问题;12.5%的学生处于水平1,即学生只能用一种方法解决三角形面积问题,多数学生选择用三角形面积公式或把三角形转化为平行四边形;21.4%的学生处于水平2,即学生只能用两种方法解决三角形面积问题,多数学生选择用三角形面积公式和把三角形转化为平行四边形;57.2%的学生处于水平3,即学生能用三种及以上的方法解决三角形面积问题,多数学生选择用三角形面积公式、把三角形转化为平行四边形、把三角形转化为长方形等。
三、借助大数据改进教学活动
测评工具的开发和运用为教学活动积累了大量有效的数据,有利于教师通过教学精准化改进教学活动。
(一)定位教学短板,增加活动体验
基于课时作业中的表现性任务,教师可以清晰地看到教学短板。例如,第一个表现性任务“理解平行四边形面积公式的推导过程”,39.3%的学生处于水平3,因此教师在后续的“平行四边形的面积”教学过程中要让学生经历“确定目标图形为长方形—把现有的平行四边形转化为目标图形长方形—验证现有图形与目标图形面积是否相等”的全过程,从而把现有的平行四边形成功地转化为目标图形长方形,再沟通平行四边形与长方形之间的对应关系,最后利用目标图形长方形的面积计算公式解决现有平行四边形的面积计算问题。
又如第二个表现性任务“用平行四边形的面积知识解决问题”,53.6%的学生处于水平3,主要问题是仅有47%的学生能在斜边上画出转化后的长方形。因此,教师在后续的“平行四边形的面积”教学过程中要鼓励学生用多种方法把平行四边形转化为长方形,尤其是要求学生掌握在平行四边形的斜边上画出转化后的长方形,并且验证平行四边形与长方形的面积是否相等。
(二)发挥数据价值,精准评价学生
教师要善于解读每个数据背后隐藏的真实思考,具体且精准地评价每个学生的学习过程。例如,针对小张同学完成“平行四边形的面积”课时作业结果给予建议:
先给予充分的肯定:小张同学,恭喜你能先找到已经学过的目标图形有哪些,再把平行四边形转化为已经学过的目标图形,还能用两种方法解决三角形面积问题。
再给予努力的方向:你还要学会验证平行四边形是否变成了学过的目标图形;学着能画出相对应的“转化后的长方形”,并写出相对应的面积计算方法。
同时,教师为学生及时推送相应的练习巩固题,如小张同学在解决第二个表现性任务时,他不能画出相对应的“转化后的长方形”,也不能写出相对应的面积计算方法。教师可以为小张同学提供类似的练习题。
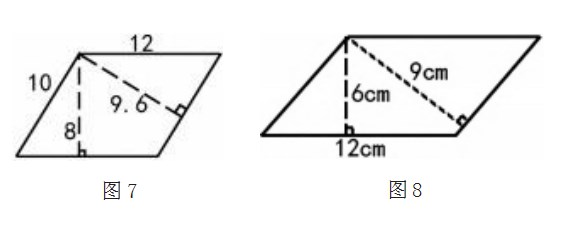
(1)用2种方法计算平行四边形的面积(见图7)。(单位:厘米)
(2)用铁丝围成一个平行四边形,如果还是用这根铁丝围一个正方形,这个正方形的面积是多少平方厘米?(见图8)
(三)基于作业分析,调整评价框架
基于学生完成课时作业的分析,得出调整后的作业评价框架(见表8)。
接下来的课时作业的表现性任务应参照上述评价框架展开适度的修改和完善。
总之,基于素养导向的表现性评价是把每个学生看作独立的个体,他们原有的知识经验和思维方式等对外部信息加工后形成真实的思维过程,教师需要尊重每个学生在表现性任务中呈现的结果,关注他们学习过程中的个性与共性,动态化地评估每个学生的学习过程和结果,促使每个学生自信地形成必备的数学素养。
参考文献:
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2]史宁中,曹一鸣.义务教育数学课程标准(2022年版)解读[M].北京:北京师范大学出版社,2022.
[3]葛素儿.基于素养立意的小学数学单元测评工具的研发与应用[J].教学月刊,2021(1):82-86.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/77022.html