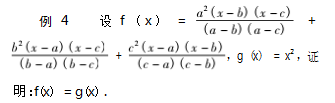SCI论文(www.lunwensci.com)
摘 要 : 数学运算是一种逻辑推理,学生在学习过程中普遍存在问题.为了使学生更好地理解 数学运算素养,提升运算素养水平,本文从数学运算的方向、方法和程序的角度,培养学生思维的广 度、敏捷度和深度,结合实例来探讨“数学运算”素养如何在教学中落地.
关键词 : 核心素养,数学运算,教学,落地
我们在教学过程中常常遇到一个让人困惑的现 象 : 对于很多题目学生知道运算方法,但总是算不下 去,或是运算出错,做得不够完整,解答过程不够规 范,等等,呈现出一种“会而不对,对而不全,全而不 规”的特点,这是数学运算能力问题.教师在执教过 程中,经常会跟学生强调数学运算能力的重要性,也 给了学生充足的时间让其运算,但这样还远远不够.
在《普通高 中课程标准(2017 年版 2020 年修 订) 》中,数学运算作为六大核心素养之一,是数学 的基本能力,是学生借助运算培养解决问题的能力. 课标明确指出数学运算是指确定运算对象,由运算 法则解决问题的素养.它包含: 运算对象、方向、方法、 程序、运算结果等等.数学运算能力的培养,能促进思 维品质的提升.而学生主要是在运算方向、运算方法以 及运算程序上出现了问题,本文以这三点为载体,结合 具体例子,谈谈教师除了在“意识”上重视数学运算之 外,如何在“行动”上落实数学运算素养的培养.
1 实例分析
数学运算是一种演绎推理、也是逻辑推理的呈 现形式,根据规则运算每一步,最终得到数学问题的 结果.学生恰恰是因为抽象能力不够、运算方向感不 强、整理化简能力欠佳等原因导致了运算的错误.比如三角函数边角互化的问题中,学生总是算到中途 就不知道往哪个方向走了 ; 解析几何运算时只知道 “联、化、判、韦”,但是在运算方法的选择上却不够 灵活,导致计算量人为加大,等等.下文针对这一现 象做具体阐述和对策分析.
1.1 多角度寻求运算方向,培养思维的广度
思维的广度是指从多方面思考一个问题.对这 个问题的事实作多方面的说明,用多种方式表述这 个问题的条件、可能的思考方向,能找到多种角度下各 种不同的解法.在教学过程中,要注重培养学生多思考 问题以及多角度探究运算方向,挖掘思路清晰且运算 量小的方法,以培养学生的运算能力和思维的广度.
例 1 ΔABC 的内角 A,B,C 的对边分别为 a,b,c,已知 sin(A + C) = 8 sin2B/2.,求 cosB.
分析 首先明确运算方向—— 求 cosB,即要保 留角 B 或 cosB,故先把 sin(A + C) 写成 sinB,得 sinB= 8 sin2 B/2.接下来该从哪个方向来求 cosB,是本题的核心所在.
解析 若是由降幂公式得 sinB = 4 ( 1 -cosB) , 那么接下来可考虑从以下三个方向着手.
点评 方向 1 出现“算不下去”的原因有: ( 1) 没有明确运算方向,正确的运算方向是求 cosB,而 不是直接求角 B; (2) 受到辅助角公式的影响,形成 了定式思维,看到这样的形式,就想到辅助角公式, 这也是很多学生思维受阻的原因.方向 2 通过两边平 方,消去了 sinB,得到了关于 cosB 的方程,是个很好的 思路,不足的是如果学生因式分解掌握得不好,算出结 果需要一定的时间,而方向 3 正好弥补了这一点,先约去1-cosB,简化了运算.方向 4 先用二倍角公式求出 tanB/2=1/4.再求 cosB,方向明确,而且运算量不大.
多角度地探究运算方向,在探究过程中,探寻方 向性强且运算量小的方法,是解题教学的重要任务, 也是培养学生思维广度的有效途径.
1.2 合理选择运算方法,培养思维的敏捷度
数学思维的敏捷性是指思维、智力活动的灵敏 程度,体现在思考问题时不固执己见,能随机应变、 触类旁通,不拘泥于某一固定形式或模式. 在解题 教学中,合理选择运算方法,减少运算量,以及对问题 的一题多解,发散思维,都可以培养思维的灵活性.
解析几何运算量较大,很多学生容易出现“算 不下去”或算错的情况,往往不能得到正确答案,或 得到了正确答案,但花费了很长的时间.出现这一现象的原因是没有选择合理的运算方法.那么在教学 中,应该怎么解决这一问题呢? 除了多训练计算能 力外,更需要多思考、多总结.比如,若直线过定点 M(0.m) ,则设其方程为 y = kx + m,若直线过定点 N(n,0) ,则设其方程为 x = ky + n ; 若有两个点都在 圆锥曲线上,可选择“点差法”; 若遇到中点,则选“中点 弦公式”; 若遇根式,可选换元法或整体运算等等.
点评 先由已知得 A,B 两点坐标的关系,再用 “整体消元法”,不需要与椭圆联立,过程简洁,运算 量小,优化了解法 1.
2 依据本质设计运算程序,培养思维的深度
思维的深度在具体问题中表现为 : 对问题提炼 的深度、抽象程度和逻辑思考水平,即思考问题的深 度和难度.依据问题的条件、现象,思考问题的本质 和联系,是思维深度与否的主要体现.我们在教育教学活动中,老师应该由外及里,由一点向多角度发 散,提炼题目的本质和规律,可以采用的运算程序, 以达到培养深度思维的目的.
例 3 已知函数f(x) = ex -ln(x + m) ,当 m≤2 时,证明f(x) >0.
解析 当 m≤2 时,ln(x + m) ≤ln(x + 2) ,所以 f(x) = ex -ln(x + m) =ex -ln(x + 2) ,故只需证明 当 m = 2 时,f(x) >0.
点评 本题的关键是证明当 m = 2 时f(x) >0. 即证 ex >ln(x + 2) .那么 m = 2 是怎么得到的呢?
由人教 A 版选择性必修第二册 99 页第 12 题得 ex =x +1 ①
当且仅当 x = 0 时等号成立.
又由人教A 版选择性必修第二册94 页第2 题得x - 1=lnx,把 x 换成 x + 2.得到 x + 1=ln(x + 2) ②
当且仅当 x = -1 时等号成立.
根据①②式,可得 ex >ln(x + 2) .
(这是因为①和②等号成立的条件不同,即两 式不能同时取到等号) .
如果我们知道该题的教材背景,则只需要证明 ①②两式成立即可( 教材上的题目) ,那样就可以简 化运算,降低思维难度.因此只要抓住了问题的本 质,揭示问题的背景,从而可以为我们的解题提供新 思路、新方法,减少运算量.
分析 如果按常规思路去分母来证明,运算量很大,很麻烦.此时就需要探寻问题的本质,抓住问 题的核心,方可简化运算.
证明 注意到f(a) = a2.f(b) = b2.f(c) = c2.又 f(x) 为次数不超过2 的多项式,故f(x) = x2 = g(x) .
点评 此题的核心所在是挖掘、发现f ( a) = a2 ,f( b) = b2 ,f ( c) = c2 ,然后利用“多项式恒等定 理”来证明这两个多项式相等. 多项式恒等定理即 : 如果两个次数不超过 n 的多项式有 n + 1 处取值相 等,则这两个多项式相等.这就抓住问题的本质,发 现解题的新思路、新方法,从而减少运算量.
数学核心素养与数学基本思想、数学思想方法 等密切相关.数学核心素养是数学基本思想在学习 某一个或几个领域内容中的具体表现 ; 数学思想方 法则是体现如何从操作层面上实现核心素养、基本 思想方法 ; 数学核心素养是数学育人阶段性的凝练, 是以往“五大数学能力”( 抽象概括、逻辑推理、数据 处理、运算求解、空间想象) 的拓展.数学核心素养 之一的数学运算在培养学生数学品质上有着重要的 意义和价值.
在培养学生的数学运算能力时,应重视学生思 维的广度、敏捷度和深度的培养,这些品质紧密相 连,密不可分.缺乏了思维,数学就不是数学,就没有 生命和活力.教师在教学过程中,应重点对学生的 “思维的过程”进行教学设计,课堂教学的每个环节 也应立足培养学生的思维品质,实现“数学运算”素 养在教学中落地生根.
参考文献 :
[1]洪燕君,周九诗,王尚志,鲍建生.普通高中数学 课程标准(修订稿) 的意见征询: 访谈张奠宙先 生[J].数学教育学报,2015.24 (3) : 39-35 .
[2] 陈玉娟.例谈高中数学核心素养的培养,从课堂 教学中数学运算的维度[J].数 学通报,2016 (8) : 34-36.54 .
[3]马云鹏.关于数学核心素养的几个问题[J].课 程·教材·教法,2015(09) : 36-39 .
[4]朱潇,李鸿昌.从数学运算素养的内涵,谈运算 能力的培养[J].中学数学,2018(01) : 57-59 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/75067.html