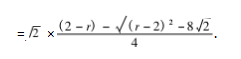SCI论文(www.lunwensci.com)
摘 要 : 随着教育体系的不断发展,逆向思维逐渐成为当今教师开展教学工作开展的重点内 容.作为学生问题分析、问题解决的基本能力,逆向思维摆脱传统单向思维的束缚,学生可以另辟蹊 径,转换思维,快速找到问题的突破口.文章立足数学学科教学,围绕当下课堂教学现状,从多个切 入点予以逆向思维的渗透,旨在强化学生的解题能力,提高学生的核心素养.
关键词 : 初中数学,解题教学,逆向思维,培养策略
逆向思维是一种创新性思维方式,旨在帮助学 生摆脱传统思路的束缚,从事物的另一面入手,回推 其发展过程,并从中发现新的原理、新的方法、新的 思路.数学作为一门逻辑学科,于学生能力、素养发 展有着十分重要的现实意义,而解题教学作为初中 数学教学的重要组成部分,一直以来都是一个教育 难点,尤其对于现阶段初中学生来说,自我思考、自 我总结能力的不足,使得他们常花费大量时间进行 知识记忆,学习质量难以得到保障.同时,从课堂教 学这一层面来看,部分教师仍沿用传统“知识讲授 + 阶段练 习”的教学模式对学生数学思维予以启 发,然而方式的单一、机械化难以有效调动学生学习 积极性,极易使他们陷入认知困境,对知识的理解、 运用流于表面.而逆向思维的渗透,能够帮助学生更 好地了解数学知识间的逻辑关系,并在思考、论证、 方案制定等环节中形成完整的知识体系,对于同类型问题也能依托自身的力量进行解决,进而提高对数学学习的自信心.对此,教师应注重逆向思维的渗透,从教学内容、教学方法予以优化,充分发挥教学 情境、导学问题等教育元素的引导作用,帮助学生摆 脱被动式学习的束缚,提升课堂教学质量.
1 初中数学解题教学中逆向思维培养原则
1.1 阶段性原则
在初中教学过程中,教师应遵循阶段性原则,依 照教学内容、课程标准进行问题设计,给予学生足够 的思考时间,同时要对学生思考过程予以记录,一方 面提高学生的课堂参与度,确保教学工作的顺利开 展 ; 另一方面避免问题分析太快,学生难以跟上,进 而影响自身解题能力的提升[1].同时,教师也要处 理好各教学环节的时间配比,注重学生思维的启发 与定理的证明,逐步进行知识拓展,从而提高课堂教 学成效.
1.2 自主性原则
学生作为课堂主体,其对教学工作的顺利开展 有着十分重要的作用.在实际教学中,教师应以“尊重学生课堂主体地位”为原则,加强学生自主思考 能力的提升,渐退适时,依托教学情境、导学问题多 元性的特点,改善“问答式”的互动方式,调动学生 学习积极性,使其主动参与到课堂学习中[2].同时, 在对问题分析、解决方案制定等环节中,教师还应引 导学生从不同角度探索解题新思路,并在小组内部 进行经验分享,以此帮助学生搭建良好的知识框架, 为其逆向思维的培养奠定基础.
1.3 延展性原则
逆向思维作为学生知识能力的综合体现,更是 其学科核心素养发展的关键品质.在实际教学中,教 师也要遵循延展性原则,摆脱教材知识的束缚,依托 多种教学技术,加强教学资源的开发与教学服务的 应用,并对现有的教学方法予以创新,如 : 依托翻转 课堂,鼓励学生自定教学方案,并围绕教学目标进行 习题设计,以此提高自身解题能力.
2 初中数学解题教学中逆向思维培养策略
2.1 逆向分析方程,强化解题能力
方程作为初中数学知识的重要组成部分,也是 学生数学模型建立的重要方法.其中,一元二次方程 作为方程的组成部分,也是初中数学教师教学的重 点.以往的教学模式下,老师常常会根据教学内容及 课程标准,根据教材知识点分布展开教学,然而学生 间能力的“多元化” ,使得他们对知识理解、运用情 况存在差异,加之自我思考能力的不足,一些学生面 对方程中的未知数无从下手,也不清楚该运用哪些 知识点[3].对此,教师可从方程问题的双向性入手, 将逆向思维运用到方程教学中,启发学生数学思维, 提高他们的解题能力.
例如,教师可设计如下方程题 :
已知关于 x 的方程 2x2 + (r-2) x + ■= 0 的两 个根分别为正方形的内切圆半径和外接圆半径,求 r 的值.若按正向思维进行求解,则根据题目信息可列 出如下方程 :
这种方式过于冗杂,且多数学生很难列出正确 的方程.对此,教师可借助逆向思维,带领学生梳理 题目关键信息,思考根与系数的关系,将正方形内切 圆半径设为 R , 列出以下方程组 :
通过代入法可求出 r = -根号2.通过这种方式,学 生能够更为清晰直观地感受到逆向思维解题的便捷 之处,不但能深化他们对解方程思路的认知,而且还 能达到提升其计算能力的目的,可谓是一举两得.
2.2 逆向梳理信息,促进思维发散
对于初中生而言,解应用题是他们的一个学习 难点.可以说,做好应用题解题教学是提高初中数学 教学有效性的必要途径,也是学生解题能力提升的 关键.由于应用题往往需要学生运用灵活的思维来 提取一些关键信息,所以教师不但要做好正向思维 的引导,而且也要将逆向思维引入到应用题解题教 学中来,使学生更好地理解题目中的数量关系,为其 解题正确率的提升以及思维能力的发展注入活力.
例如,教师可结合日常生活设计如下应用题 :
某人乘坐飞机,自身携带了 30 公斤行李,而飞 机免费行李额是 20 公斤,超重的部分每公斤按照票 价的 1.5% 来收取费用.该乘客缴纳了 120 元的行 李超重费,求该乘客的飞机票价格是多少? 在讲授 该题时,教师可引入逆向思维,首先与学生一同提取 其中的关键信息 :
120 元超重费、30 公斤行李、20 公斤免费行李 额、1.5% 票价费用.
随后,教师可提问学生 120 元对应多少公斤的 行李重量?
即 30-20 = 10( 公斤) .
然后,再让学生进行票价计算 ;
即 120 ÷ 10 ÷ 1.5% = 800 元.
通过问题的逐步引导,帮助学生更好地梳理题目信息间的逻辑关系,以此促进他们数学思维的多 向化发展,提高学习积极性与自信心.
2.3 逆向逻辑推理,提高学生空间想象能力
几何问题是初中学生学习的难点,需要学生 具备良好的空间想象能力.对此,教师在 实 际教 学中,应注重学生思维的启发,同时融合逆向思 维,降低学生学习难度的同时,便于学生理清题 设与结论之间的复杂关系,并通过逆向思维获得 解题新思路.
对此,教师可设计如下例题 :
如图 1.已知 : ΔABD 与 ΔAEC 都是等边三角 形,求证 : BE = DC.
在讲解时,教师可先让学生在图中标注已知信 息,并借助已学知识,尽可能地推理出其他信息.随 后,教师可设置阶段性的导学问题,依托逆向思维, 引导学生执果索因.
如 : 要 想 证 明 BE = DC,就 要 证 明 ΔABE ≌ ΔADC,而要想证明上述两个三角形全等,就要从边 和角的关系入手.这样通过梳理,便可明确本题的目 标为 :
证明 :AD = AB; ∠2 + ∠3 = ∠ 1 + ∠2;AC = AE
随后根据题目信息,ΔABD、ΔAEC 为等边三角形,便可层层推导出 BE = DC.
通过这种逆向推理的方法,既能帮助学生建构 良好的思维,又能有效简化证明过程,提高他们的逆 向思维能力,使其在日后面对此类题目时更加得心应手.
2.4 优化课后评价,提升核心素养
教学评价的改革对于数学教学质量的提升有重 要作用.新时代背景下,教师要改革以往的评价理 念,革新教学评价体系,通过这种方式助力学生个性 发展.
首先,注重褒贬合一,提升评价指向.在初中数 学教学过程中,教师应避免一味地奖励或批评学生, 注重其课堂主体地位,转变传统的评价模式,同时给 予学生足够的尊重,进而提高他们的学习体验[4]. 从另一个角度来看,考试评价是对学生上一阶段学 习情况的总结与分析,因此教师在制定评价内容时, 应立足学生能力、素养发展需求,融入赏识教育、差 异化教育等教育理念,帮助学生正确认识自己,明确 发展目标.
其次,拓宽评价形式,注重共 同参与.新课标 背景下,教师要进一步优化课堂评价模式,结合 学科特点、考试要求,制定预设评价与生成评价, 例如,预设评价,教师应根据教学进度、学生学 习 情况初步拟 定,如 : 学生是否掌握该 知识 点? 学 生考试过程中是否会出现分析时间过长等.生成 评价则要根据学生能力提升情况进行制定,且 需 要在预设评价反馈的基础上予以深化,同时加强 其数学思维的培养,以此提高评价对学习的促进 作用.
总之,将逆向思维渗入到初中数学解题教学中 有着诸多现实意义.初中数学教师应明确当下教学 工作的出发点与落脚点,深入解读逆向思维的特点 与实施原则,依据数学知识特点进行有效渗透,摆脱 传统“知识主导”教学架构的束缚,降低学生学习难 度,发散其数学思维,以此促进其数学综合能力的全 面提升.
参考文献 :
[1]李文江.浅谈初中数学教学中学生逆向思维能力的培养[J].试题与研究,2022 (31) : 4-6 .
[2]马子健.逆向思维在初中数学解题教学中的应 用探究[J].科学咨询(教育科研) ,2022 ( 10 ) :210-212 .
[3]扈学慧.如何在数学解题中有效利用逆向思维方式[J].数理化解题研究,2022 (26) : 5-7 .
[4]梁玲.初中数学解题中逆向思维的应用[J].数 理天地(初中版) ,2022 (16) : 51-52 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/74934.html