SCI论文(www.lunwensci.com):
摘 要 : 极值点偏移问题综合性较强,难度较大,经常作为压轴题出现在高考试卷中.解决此类 问题主要有以下几种方法 : 辅助函数法、对称函数法、对数均值不等式法、差比换元法.
关键词 : 极值点偏移; 构造; 换元
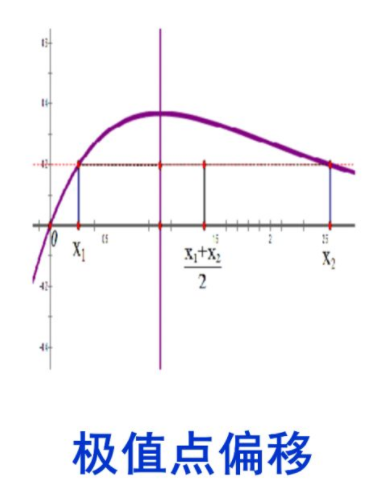
极值点偏移就是函数在极值点左右的增减速度 不一样,导致函数的图象不具有对称性,从问题设置 分类,极值点偏移问题主要有加法型、减法型、平方 型、乘积型和商型[1].每种类型的试题都有通解和 特殊解法,本文通过探析 2022 年全国甲卷理科数学 第 21 题的多种解法介绍处理极值点偏移问题的几种解题策略.
1 试题呈现及分析
题目 (2022 年全国高考甲卷理科数学 21 题)
已知函数f( x) =

-lnx + x-a.
( 1) 若f( x) =0,求 a 的取值范围 ;
(2) 证明 : 若f( x) 有两个零点 x1 ,x2 ,则 x1 x2 <1.
试题分析 试题中函数f(x) 解析式以指数函 数、对数函数和幂函数通过加法、减法、乘法和除法 运算构成,第( 1) 问考查恒成立问题求解参数的取 值范围 ; 第(2) 问在第( 1) 问的基础上,考查乘积型 的极值点偏移问题,极值点偏移问题的解答方法多 样,但每种方法都要求学生有极高的变形技巧,下面 对第(2) 问一一介绍各种解答方法.
2 多解探究
2.1 第(1) 问解法
2.2 第(2) 问解法
分析 1 由第( 1 ) 问知g (x) =

-lnx + x 在(0,1) 上单调递减,在( 1,+ ∞ ) 上单调递增,由于 f(x) 的单调性与 g(x) 相同,所以f(x) 的两零点 x1 , x2 分别在 x = 1 两侧,不妨设 0 <x1 < 1 <x2.要证x1 x2 < 1,即证 0 <x1 <
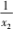
< 1,只 需证 明 f (x1 ) >f(
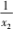
) ,即证f(x2 ) >f(
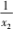
).可以构造辅助函数 F(x)=f(x) -f(

) (x >1) 直接证明
点评 构造辅助函数是处理极值点偏移问题的 通法,此方法的重点在于将证明多元变量不等式x1 x2 <1 转化为证明单元变量不等式f(x2 ) <f(
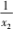
) ,进而可以构造辅助函数直接证明.
分析 2 令 h(t) = et + t -a,t(x) = x -lnx,易 知 t(x) 在(0,1) 上单调递减,在( 1,+ ∞ ) 上单调递 增,h(t) 在 ( 1,+ ∞ ) 单调递增,因此,由 f ( x1 ) = f( x2 ) 可得 t(x1 ) = t(x2 ) ,即 x1 -lnx1 = x2 -lnx2.要 证 x1 x2 <1,需证 lnx1 + lnx2 <0.令 u = lnx,m( u) = eu -u,则原问题转化为若 eu1 -u1 = eu2 -u2 ,即 m(u1 ) = m(u2 ) ,证明 u1 + u2 <0,可构造对称函数 H(u) = m(u) -m( -u) (u>0) 加以证明.
解法 2 ( 构造对称函数) 由f ( x1 ) =f ( x2 ) 可 得 t(x1 ) = t(x2 ) ,即 x1 -lnx1 = x2 -lnx2 成立.假设 0<x1 <1<x2 ,要证 x1 x2 <1,需证 lnx1 + lnx2 <0.
令 u = lnx,m ( u ) = eu - u,所 以 m ( u1 ) = m(u2 ) ,下证 u1 + u2 <0.
构造对称函数 H( u) = m( u) -m( -u) ( u > 0) ,H ' (u) = m ' (u) -m ' ( -u) = eu + e-u -2>0.
所以 H( u) 在(0,+ ∞ ) 上单调递增,H ( u) > H(0) = 0.
当 u >0 时,m ( u) -m ( -u) >0,即 m ( u) > m( -u) ,所以 m(u2 ) >m( -u2 ) .
又因 为 m ( u1 ) = m ( u2 ) ,所 以 m ( u1 ) > m( -u2 ) .
由于 m(u) = eu -u 在( - ∞ , 0) 上单调递减,所 以 u1 <-u2 ,即 u1 + u2 <0.得证.
点评 构造对称函数也是处理极值点偏移问 题的通法,本题中由f ( x1 ) =f ( x2 ) 可得 x1 -lnx1 = x2 -lnx2 成 立,再 将 证 明 x1 x2 < 1 转 化 为 证 明 lnx1 + lnx2 <0,进而可以通过构造对称函数进行证 明.需要注意的是,构造对称函数法若找不到极值点将失效,需要寻找其他解法.
分析 3 由解法 2 可知 x1 -lnx1 = x2 -lnx2 成立,即
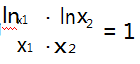
成立.要解决此类双变量不等式问题,可以尝试从不等式的角度出发,本题可以考虑 对数均值不等式.如果令 u = lnx,则 eu1 -u1 = eu2 - u2 ,要证 u1 + u2 <0,此时还可以尝试运用指数均值 不等式证明.
解法 4 ( 指数均值不等式) 要证 x1 x2 <1 ,需 证 lnx1 + lnx2 <0 ,令 u1 = lnx1 ,u2 = lnx2 ,即证 u1 + u2 <0 .
点评 在处理原函数中同时含有幂指对的极 值点偏移问题时,可以通过幂指对互化的方法将原 函数形式进行适当变化,将其转化为常见不等式的 模型,并运用不等式进行证明,这样可以将不同的题型转化为同一类型,简化解题过程.
分析 4 对于极值点偏移问题,可以依据已知 条件f(x1 ) =f(x2 ) ,得到关于 x1 、x2 的等式,再利用比值换元
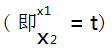
或差值换元( 即 x1 -x2 = t) 将x1 、x2 替换为含 t 的函数加以证明.
点评 以上两种解法均是从处理多变量函数问 题的角度入手,引入参数 t 将多元函数问题转化为 一元函数问题,即在得到 x1 、x2 关于 t 的等量关系 后,直接证明 x1 x2 <1.
突破极值点偏移问题,不仅要掌握每种类型试 题的通用解法,更要掌握常见解法所蕴含的数学思 想,如转化思想、数形结合思想、消元思想等[2].另 外需要掌握一些常见不等式放缩,如对数不等式、基 本不等式、切线不等式、糖水不等式等.在教学中,还 要立足教材,注重通性通法.
参考文献 :
[1]王丽君.再谈极值点偏移问题[J].理科考试研 究,2019,26(05) : 9 -10 .
[2] 胡贵平.2021 年全国新高考 I 卷导数题的几种 解法[J].理科考试研究,2021,10(01) : 2-4 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/72803.html
 -lnx + x-a.
-lnx + x-a.
 -lnx + x 在(0,1) 上单调递减,在( 1,+ ∞ ) 上单调递增,由于 f(x) 的单调性与 g(x) 相同,所以f(x) 的两零点 x1 , x2 分别在 x = 1 两侧,不妨设 0 <x1 < 1 <x2.要证x1 x2 < 1,即证 0 <x1 <
-lnx + x 在(0,1) 上单调递减,在( 1,+ ∞ ) 上单调递增,由于 f(x) 的单调性与 g(x) 相同,所以f(x) 的两零点 x1 , x2 分别在 x = 1 两侧,不妨设 0 <x1 < 1 <x2.要证x1 x2 < 1,即证 0 <x1 < 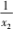 < 1,只 需证 明 f (x1 ) >f(
< 1,只 需证 明 f (x1 ) >f(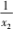 ) ,即证f(x2 ) >f(
) ,即证f(x2 ) >f(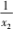 ).可以构造辅助函数 F(x)=f(x) -f(
).可以构造辅助函数 F(x)=f(x) -f(  ) (x >1) 直接证明
) (x >1) 直接证明

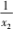 ) ,进而可以构造辅助函数直接证明.
) ,进而可以构造辅助函数直接证明.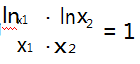 成立.要解决此类双变量不等式问题,可以尝试从不等式的角度出发,本题可以考虑 对数均值不等式.如果令 u = lnx,则 eu1 -u1 = eu2 - u2 ,要证 u1 + u2 <0,此时还可以尝试运用指数均值 不等式证明.
成立.要解决此类双变量不等式问题,可以尝试从不等式的角度出发,本题可以考虑 对数均值不等式.如果令 u = lnx,则 eu1 -u1 = eu2 - u2 ,要证 u1 + u2 <0,此时还可以尝试运用指数均值 不等式证明.


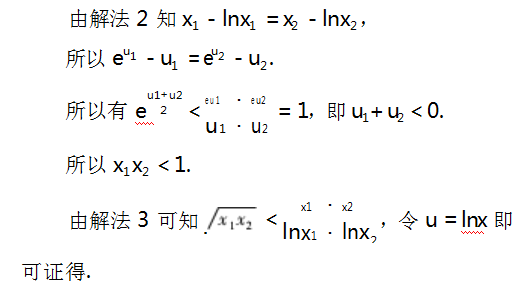
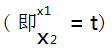 或差值换元( 即 x1 -x2 = t) 将x1 、x2 替换为含 t 的函数加以证明.
或差值换元( 即 x1 -x2 = t) 将x1 、x2 替换为含 t 的函数加以证明.



