SCI论文(www.lunwensci.com):
摘 要:高等代数是数学系大一新生的必修科目,每一位高中数学教师都学习过这门课程.但 是,大部分数学教师认为:大学数学知识与高中数学没有太大联系,故线性代数的知识早已被抛到 九霄云外.当然,这样的认知是很自然的,因为在大学课本中鲜有介绍线性代数理论在初等数学中 的应用.新课程标准中提到:高中数学课程的基本理念之一是—构建共同基础,提供发展平台.为了满足部分对数学有兴趣的学生更高的数学需求,在人教版《普通高中课程标准实验教科书 ·矩阵与变换(选修 4 - 2) 》中介绍了一些简单的二阶矩阵知识,但现行的新版教材中将这块内容删掉了.本文将介绍利用线性代数中的矩阵理论解决初等数学中的部分经典问题.
关键词:矩阵;线性代数;数列
由于本文涉及线性代数中矩阵的知识,若有需 要,可参考本文的参考文献[1] , 当然也可以选择其 它的高等代数或线性代数教材.与微积分一样,矩阵 也是数学知识体系中非常有力的工具.笔者将介绍 矩阵理论在求数列通项中的应用以及在分式线性函 数迭代中的应用.
1 二阶矩阵的幂
为了方便本文定理的证明,这里,我们先介绍二 阶矩阵幂的求法.我们将二阶矩阵 A 分为两种类 型,类型一:复数域上的二阶矩阵 A 有两个不相等 的特征根;类型二:复数域上的二阶矩阵 A 有两个 相等的特征根.为了求这两种类型的二阶矩阵的任 意次正整数幂,我们给出以下引理.
引理 1 若复数域上的二阶矩阵 A 有两个不相 等的特征根 x1 与 x2 , 则存在某个可逆矩阵 T, 使得
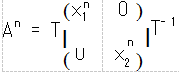
由线性代数知识知,矩阵 T 就是二阶矩阵 A 的 两个特征向量构成的矩阵,容易求得.再由公式
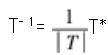
, 即可求出 T- 1(其中 T 指矩阵 T 的行列式,T ∗ 指矩阵 T 的伴随矩阵).也就是说,类型一 中 的二阶矩阵 A 的任意有限次正整数幂由引理 1 彻底 解决.接下来笔者将介绍类型二中的矩阵 A 的任意有限次正整数幂的求法.
引理 2 若复数域上的二阶矩阵
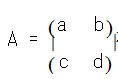
有两 个 相 等 的 特 征 根 x0 , 则
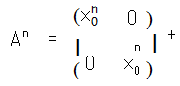

引理 2 彻底解决了类型二中的二阶矩阵 A 的任 意有限次正整数幂.至此,我们彻底解决了复数域上 的二阶矩阵的任意有限次正整数幂问题.在具体解题 时,不必背引理 1 和引理 2,只需掌握求解方法即可.
2 二阶矩阵在分式线性函数迭代中的应用
引理 3 记 f( x )=

,f1( x )=f( x ),f2( x )=f[f1( x )],…,fn( x )=f[fn - 1( x )],若记 f( x )对应的 矩阵为
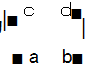
, 则 fn( x )对应的矩阵为
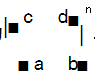
例 1 已知

,记 f1( x )=f( x ),f2(x)=f[f1(x)],…,fn(x)=f[fn -1(x)],求f10(x).
解 由引理 3 知,我们只需求
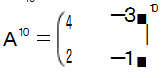
即可求得 f10( x ).而矩阵 A 的特征方程 x2 -3 x +2 =
0 的两根为 x 1 =1 ,x2 =2.接下来我们可以利用引理 1 的方法,求得矩阵 A 属于特征根 x 1 =1 的特征向量为线性方程组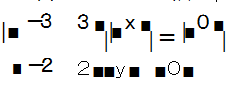 的 一 个基础解系
的 一 个基础解系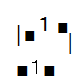 ,矩阵A属于特征根 x2 =2 的特征向量为线性方程组
,矩阵A属于特征根 x2 =2 的特征向量为线性方程组
笔者对例题的编写源于引理 3 ,由例 1 我们看 到,矩阵理论在初等数学中也大有用武之地,是解决 很多数学问题强有力的工具.虽然在高考中不会出 现这样的考题,但是矩阵理论之于热爱数学的学生 和教师而言可以开阔视野,激发学习与研究数学的 兴趣,是大有裨益的.
3 特征根法求数列的通项公式
在多数高中数学竞赛教材中都有提及利用特征 根法求二阶实系数线性递推公式的数列通项问题. 比起待定系数法而言要简单许多,只需记住几个简 洁的结论即可快速解题,深受竞赛学子的追捧.但是 多数竞赛教材并未提及该方法的来源,这令多数阅 读教材的师生仅知其然而不知其所以然.笔者将于 此给出一个满意的解答.
方法二 ( 矩阵法,揭示结论来源)我们将数列
方法二 ( 矩阵法,揭示结论来源)由复数域上多项式根与系数的关系:p = 2x0 , q = - x
0 , A n - 2 =
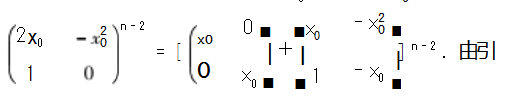
定理 1 的两个小结论都采用了两种方法进行证 明,其中方法一高中生亦能理解,但是留给我们一连 串巨大的问号.是谁这么聪明发明了这个方法? 数 列的特征根又是什么? 事实上从方法二就能看出特 征根法求数列通项的本源,数列并没有特征根,特征 根是矩阵的.定理 1 只是用初等数学的语言将结论 表示给中学生看,它的优点在于避开了高等数学,但 笔者认为作为数学教师,追本溯源才能真正理解该 方法的本质,才能发现更多类似定理 1 的有趣结论. 事实上,数列可以理解为一种特殊的矩阵,故矩阵理 论在数列中的应用是非常广泛的.对于这些中学课 本与大学课本都未涉及的经典应用,笔者将给出以 下例题.
例 2 求著名的斐波那契数列的通项:已知 a1 = a2 = 1 , a n + 2 = a n + 1 + a n 求 a n .
由例 2 , 例 3 我们看出,用特征根法求二阶线性 递推公式的通项是多么的简洁,求系数 A 与 B 时不 必背定理 1 的结论,只需使用待定系数法求解即可.
由例 4 , 例 5 我们看出 ,非齐次的二阶线性递 推公式以及部分非线性的递推公式求通项只需 稍作处理 即 可 转 化 为 齐 次 线 性 递 推 公 式.至 此 , 定理 1 即可 彻 底 解 决 二 阶 线 性 递 推 公 式 求 通 项 的问题.当然例 3 的解法很多 ,例如我们可以使 用母函 数 法 ,这 将 涉 及 数 学 分 析 中 的 幂 级 数 理 论 ,且计算 量 较 特 征 根 法 要 大 很 多 ,这 里 就 不 作 介绍了 ,感 兴 趣 的 读 者 可 参 考 本 文 的 参 考 文 献[ 4 ] 第 83 页例 3 . 36.
例 6 已知 a1 = a2 = 2018 , a n + 2 = - a n + 1 - a n ,求 a n .
解 特征根为
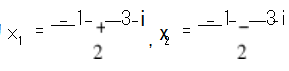
, 由待定系数法求得 A = B = - 2018.
由例 6 , 例 7 我们看出,定理 1 对虚特征根以及 虚系数的二阶线性递推公式求通项也是非常方便 的.细心的读者或许已经发现笔者编制的例 4 是周 期为 3 的周期数列,求通项的意义并不大,但是此题 仍具有一定的代表性.
5 笔者的点滴感悟
作为高中 数 学 教 师 ,笔 者 以 为 ,高 观 点 下 的 初等数学 更 显 深 刻 ,更 显 本 质.掌 握 一 些 与 高 中 数学有关的高等代数、数学分析、解析几何、初等 数论、复变 函 数、概 率 论 等 大 学 数 学 知 识 是 大 有 裨益的.于学生 ,我们倡导积极主动、勇于探索的 学习方式;于 己 ,又 何 尝 不 应 如 此? 毕 竟 ,学 习 , 是一辈子的事情.
参考文献:
[1] 张禾瑞,郝鈵新.高等代数( 第五版)[ M] . 北 京:高等教育出版社,2007.
[2] 蔡小雄,孙惠华.新课标高中数学竞赛通用教材 (高二分册,第三版)[ M] . 杭州:浙江大学出版 社,2009.
[3] 陈唐明.矩阵求法递推数列通项公式再探[ J] .高中数学教与学,2010(09) : 11 - 13.
[4] 李胜宏,李名德.高中数学竞赛培优教程(专题讲 座)(第二版)[M] . 杭州:浙江大学出版社,2009.
[5] 欧阳光中,朱学炎,金福临,陈传璋.数学分析下 册( 第三 版)[ M ] . 北 京:高 等 教 育 出 版 社, 2007.
[6] 中华人民共和国教育部.普通高中数学课程标 准( 实验)[ M] . 北京:人民教育出版社,2003.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/70835.html

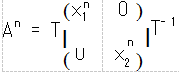
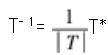 , 即可求出 T- 1(其中 T 指矩阵 T 的行列式,T ∗ 指矩阵 T 的伴随矩阵).也就是说,类型一 中 的二阶矩阵 A 的任意有限次正整数幂由引理 1 彻底 解决.接下来笔者将介绍类型二中的矩阵 A 的任意有限次正整数幂的求法.
, 即可求出 T- 1(其中 T 指矩阵 T 的行列式,T ∗ 指矩阵 T 的伴随矩阵).也就是说,类型一 中 的二阶矩阵 A 的任意有限次正整数幂由引理 1 彻底 解决.接下来笔者将介绍类型二中的矩阵 A 的任意有限次正整数幂的求法.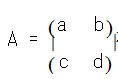 有两 个 相 等 的 特 征 根 x0 , 则
有两 个 相 等 的 特 征 根 x0 , 则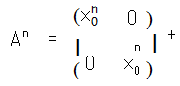

 ,f1( x )=f( x ),f2( x )=f[f1( x )],…,fn( x )=f[fn - 1( x )],若记 f( x )对应的 矩阵为
,f1( x )=f( x ),f2( x )=f[f1( x )],…,fn( x )=f[fn - 1( x )],若记 f( x )对应的 矩阵为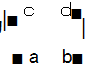 , 则 fn( x )对应的矩阵为
, 则 fn( x )对应的矩阵为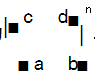
 ,记 f1( x )=f( x ),f2(x)=f[f1(x)],…,fn(x)=f[fn -1(x)],求f10(x).
,记 f1( x )=f( x ),f2(x)=f[f1(x)],…,fn(x)=f[fn -1(x)],求f10(x).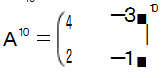 即可求得 f10( x ).而矩阵 A 的特征方程 x2 -3 x +2 =0 的两根为 x 1 =1 ,x2 =2.接下来我们可以利用引理 1 的方法,求得矩阵 A 属于特征根 x 1 =1 的特征向量为线性方程组
即可求得 f10( x ).而矩阵 A 的特征方程 x2 -3 x +2 =0 的两根为 x 1 =1 ,x2 =2.接下来我们可以利用引理 1 的方法,求得矩阵 A 属于特征根 x 1 =1 的特征向量为线性方程组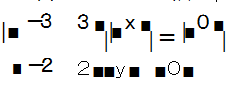 的 一 个基础解系
的 一 个基础解系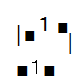 ,矩阵A属于特征根 x2 =2 的特征向量为线性方程组
,矩阵A属于特征根 x2 =2 的特征向量为线性方程组




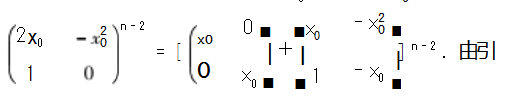




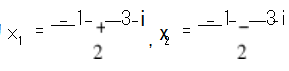 , 由待定系数法求得 A = B = - 2018.
, 由待定系数法求得 A = B = - 2018.

