SCI论文(www.lunwensci.com):
摘 要:概念学习是数学学习中至关重要的组成部分.本文以古典概型的概念教学为例,探究 概念辨析的闭环教学方法.具体以抽签问题和掷骰子问题为例,在样本空间的不同选取方法下阐述 了古典概型概念的学习过程,不断检验条件,不断辨析,从而达到闭环教学效果.
关键词:概念学习;试错教学方法;古典概型;抽签问题;掷骰子问题
1 数学概念的传统教学方式
数学概念的传统教学方法,主要采取“ 教师讲 解”的教学模式,学生主要采取“ 听课—练习”的 模式.这样,教师和学生可以快速高效地完成教和学 的任务.就古典概型这一概念来说,课堂讲解的时 候,有经验的教师会强调“ 等可能性”这 一前提条 件,然后就是举例讲解.但是在教师讲解例题的过程 中,容易忘记强调“ 等可行性”;学生在做题的过程 中,更容易忘记检验“等可能性”这一条件.
2“ 试错法”教学方式
“ 试错法”的根本原则是以学生为主体.学生根 据数学问题,用概念自行尝试、自行分析,教师对学 生的学习情况起引导作用,这样可以提高学生的自 主思考能力和自学能力.
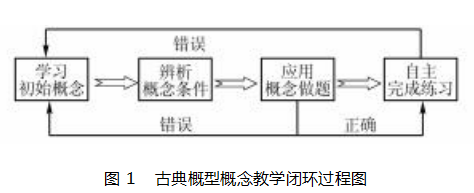
具体就古典概型的概念教学来说,概念学习的 一般过程为课前导学( 预习)、课堂概念讲解、试错 式解题、错误分析( 寻求帮助)、获取正确解题方法、 分析总结、课后练习等环节.当选取不同的样本空间 时,可能会得到错误结果.对错误原因进行分析,产 生有效提问,教师进行引导;然后找到一种或多种正 确做法;最后完成练习,形成一个闭环过程,如图 1 .
下面以古典概型的概念教学为案例,具体阐述 教学活动中的概念学习的试错教学方法.
3 教学案例
3 . 1 第一步:教师引导学生学习初始概念,即样本空 间和古典概型的概念
随机试验中的每一种可能出现的结果称为样本 点.所有样本点组成的集合称为样本空间,记为 Ω .
在中学概率中,古典概型是一种非常重要的概 率模型.如果每次试验的结果只有有限多个,并且每 个试验结果发生的可能性是相同的,那么称这种概 率模型为古典概率模型,简称古典概型.设古典概型 中样本点总数为 n , 事件 A 含有其中的 m 个样本点, 则定义事件 A 的概率为 P( A) = m/n.
3 . 2 教师引导学生辨析概念条件
在解决概率问题时,分析问题的角度不同会导 致选取的随机试验的样本空间的不同.在不同的样 本空间下,是否都能通过古典概型来计算同一个事件的概率呢?这就要看样本空间中每个样本点的发 生是否是等可能的.有的学生在解决问题的时候,以 为找到了样本空间,就可以直接利用古典概型的计 算公式来计算概率,而忽略了古典概型的概念中 “ 样本点发生的等可能性”这一前提条件.
3 . 3 第三步:学生应用概念做题
教学活动中,全班学生按小组进行讨论,提出解 题方法,写出解题过程.将有代表性的小组结论进行 展示和讨论.
3 . 3 . 1 提出数学问题
掷骰子问题:同时掷两颗骰子,求出现的点数和 为 7 的概率.
3 . 3 . 2 找样本空间并计算概率
首先,由生活经验知道,每颗骰子都有 6 个面, 分别标有数字 1 、2 、3 、4 、5 、6. 当同时掷两颗骰子时, 每颗骰子出现各个数字是等可能的.记事件 A 表示 两颗骰子点数和为 7 .
小组成果展示 1 :
考虑骰子的顺序,第一颗骰子出现的点数有 6 种不同情况,第二颗骰子出现的点数有 6 种不同情 况,因此样本空间含有 6 × 6 = 36 个样本点,具体为:
Ω 1 = { ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 1 , 5 ) , (1 , 6) , (2 , 1) , (2 , 2) , (2 , 3 ) , (2 , 4 ) , (2 , 5 ) , ( 2 , 6) , (3 , 1) , (3 , 2) , (3 , 3 ) , (3 , 4 ) , (3 , 5 ) , (3 , 6 ) , (4 , 1) , (4 , 2) , (4 , 3 ) , (4 , 4 ) , (4 , 5 ) , (4 , 6) , ( 5 , 1) , (5 , 2) , (5 , 3 ) , (5 , 4 ) , (5 , 5 ) , (5 , 6) , (6 , 1 ) , (6 , 2) , (6 , 3) , (6 , 4) , (6 , 5) , (6 , 6) } ,
A = {(1 ,6) , (2 ,5) , (3 ,4) , (4 ,3) , (5 ,2) , (6 , 1)} .
根据题意可知样本空间 Ω1 中的 36 个样本点是 等可能发生的,所以在此样本空间下,可以用古典概型来计算事件 A 的概率,并且概率为 P(A) =

=

.
教师点评:此处的分析非常好,检验了概念的适 用条件,正确使用概念解决问题.
小组成果展示 2 :
不考虑骰子的顺序,样本空间含有 21 个样本 点,具体为:
Ω2 = { ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 1 , 5 ) , (1 , 6) , (2 , 2) , (2 , 3 ) , (2 , 4 ) , (2 , 5 ) , (2 , 6) , ( 3 ,3) , (3 , 4 ) , (3 , 5 ) , (3 , 6) , (4 , 4 ) , (4 , 5 ) , (4 , 6 ) , (5 , 5) , (5 , 6) , (6 , 6) } ,
A = { (1 , 6) , (2 , 5) , (3 , 4) } .
此时概率为 P( A) =

=

.
教师点评:注意到样本空间 Ω2 中的每个样本 点都可以用 Ω1 中的样本点来表示,由此可知这 21 个样本点不是等可能发生的,所以在此样本空间下 不能用古典概型来计算事件 A 的概率.
小组成果展示 3 :
直接考虑两颗骰子点数和的不同情况,样本空 间含有 11 个样本点,具体为:
Ω3 = {2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12} , A = {7} .
此时概率为 P( A) =

.
教师点评:注意到样本空间 Ω3 中的每个样本 点都可以用 Ω1 中的样本点来表示,由此可知这 11 个样本点不是等可能发生的,所以在此样本空间下 不能用古典概型来计算事件 A 的概率.
3 . 3 . 3 教师总结
只有严谨地验证古典概型的前提条件,确保样 本空间中样本点的等可能性,才能找到符合要求的 样本空间,计算出正确的概率.
3 . 4 第四步:学生自主完成练习
抽签问题:袋中有 a 根红签,b 根白签,它们除 颜色不同外,其他方面没有差别.现有 a + b 个人依 次无放回地去抽签,求第 k 个人抽到红签的概率.
学生们认真思考,经过小组讨论,得到了如下几 种解决问题的方法.
根据题意,抽到每根签都是等可能的,因此这是 一个古典概型问题,并且问题等价于把签一根一根 抽出来排成一列,求第 k 次抽到红签的概率.记事件 A 表示第 k 个人抽到红签.
方法 1 把 a 根红签和 b 根白签看作是不同 的,那么 a + b 根不同签的所有全排列种数为( a + b) ! , 即样本空间 Ω1 含有( a + b) ! 个样本点.根据 题意可以判断每个样本点是等可能发生的,符合古 典概型的前提条件.事件 A 可以理解为:在第 k 个位置上排列的一定是红签,有 a 种排法;在其他 a + b- 1 个位置上的签的排列种数为( a + b - 1) ! . 因此,事件 A 含有 a ( a + b - 1) ! 个样本点.由古典概型公式可得

方法 2 把 a 根红签看作是没有区别的,把 b 根白签也看作是没有区别的,仍把抽出的签依次排 列成一列,这是含有相同元素的全排列.此时 a + b根签的所有全排列种数为

,即样本空间
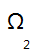
含有
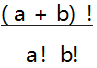
个样本点.根据题意可以判断每个样本点是等可能发生的,符合古典概型的前提条件.事件 A 可以理解为:在第 k 个位置上放红签,只有 1 种放法;在其他 a + b - 1 个位置上放余下的 a + b - 1根签,其中 a - 1 根是没有区别的红签,b 根是没有区别的白签,共有
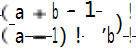
种方法,即事件 A 含有

个 样 本 点.由 古 典 概 型 公 式 可 得
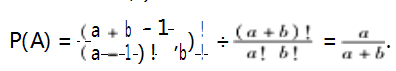
方法 3 根据题意知,第 k 次抽到红签仅与前面 k - 1 次所取的签的情况有关,而与以后抽签的情况无关.因此只需要研究前面 k 次抽签情况.把各签 看作不同,前 k 次的每一种抽签情况相当于从 a + b根不同的签中任取 k 根的全排列,共有
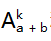
种方法,即样本空间 Ω3 含有
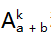
个样本点.根据题意可以判断每个样本点是等可能发生的,符合古典概型的前提条件.事件 A 可以理解为:在第 k 次取红签,有a种取法;在其他k-1次,是从a+b-1根不同的签中任取k-1根的全排列,共有
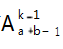
种方法,即事件A含有
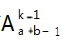
个样本点,由古典概型公式可得;

教师点评:从三种角度寻找生活中最常见的抽 签问题的样本空间,并发现样本空间中的样本点都 符合等可能性的,因此均可以使用古典概型公式计 算概率.这三种方法中,方法 1 是最常规的最容易想 到的,方法 2 和方法 3 的技巧性都要强一点. 完成练习后,仍然有“ 爱思考”的学生提出如下 质疑:
学生说:老师,第一个人抽签后,还剩下( a + b- 1) 根签.如果第一个人抽到红签,那么第二个人 抽到红签的概率就变小了;如果第一个人没有抽到红签,那么第二个人抽到红签的概率就变大了.因 此,第二次抽签的概率会受到第一次抽签结果的影 响,从而抽签问题不是公平的.
此时很多学生也深以为然.这样,就产生了冲突. 教师引导:我们后面会学习条件概率的概念.
“ 如果第一个人抽到红签,那么第二个人抽到红签 的概率就变小了”,这里的概率实际上是条件概率 了,与我们题目中的概率是不同的概率.请同学们接 下来预习条件概率并用条件概率来分析抽签问题的 公平性.
4“ 试错法”教学效果提升
传统教学中教师是主体,主导学生的概念学习; “ 试错法”教学中学生为主导,学生自主探索解决问 题.试错教学方法,让数学课堂更真实,更有趣,学生 参与度更大.缺点是会有不自觉的学生出现“ 浑水 摸鱼”现象,没有进行比较有效的思考和学习,这就 需要教师及时地观察和督促以及帮助.
一次课的教学方法的改变可能不容易区分两种 教学方式的差异,但是若长期坚持“ 试错法 ”教学 方式,学生能自主思考,提出更有深度的问题,能 更清晰正确地使用概念解决问题,那么 一 定能更 有效地培养和提升学生的自主学习能力、创新思 考能力,提升学生的数学素养.
参考文献:
[1] 缪铨生.概率与统计( 第 3 版)[ M] . 上海:华东 师范大学出版社,2014 : 7 .
[2] 沈荣泸.抽签公平性的多种解法[ J] . 数学学习 与研究,2014(23) : 72 .
[3] 姚璐,李洋.一道概率题引发的思考[ J] . 中学生数学,2020 , 9(641) : 4 - 5 .
[4] 刘长柏.从不同侧面求解古典概型[ J] . 中学生数理化,2021(3) : 6 - 7 .
[5] 刘义娟.“试错”:让数学课堂更真实、有效[ J] .教学机智,2016(5) : 42 - 43 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/70782.html

 ,即样本空间
,即样本空间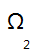 含有
含有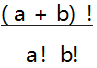 个样本点.根据题意可以判断每个样本点是等可能发生的,符合古典概型的前提条件.事件 A 可以理解为:在第 k 个位置上放红签,只有 1 种放法;在其他 a + b - 1 个位置上放余下的 a + b - 1根签,其中 a - 1 根是没有区别的红签,b 根是没有区别的白签,共有
个样本点.根据题意可以判断每个样本点是等可能发生的,符合古典概型的前提条件.事件 A 可以理解为:在第 k 个位置上放红签,只有 1 种放法;在其他 a + b - 1 个位置上放余下的 a + b - 1根签,其中 a - 1 根是没有区别的红签,b 根是没有区别的白签,共有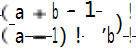 种方法,即事件 A 含有
种方法,即事件 A 含有 个 样 本 点.由 古 典 概 型 公 式 可 得
个 样 本 点.由 古 典 概 型 公 式 可 得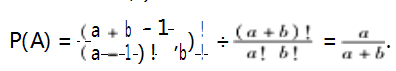
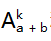 种方法,即样本空间 Ω3 含有
种方法,即样本空间 Ω3 含有 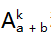 个样本点.根据题意可以判断每个样本点是等可能发生的,符合古典概型的前提条件.事件 A 可以理解为:在第 k 次取红签,有a种取法;在其他k-1次,是从a+b-1根不同的签中任取k-1根的全排列,共有
个样本点.根据题意可以判断每个样本点是等可能发生的,符合古典概型的前提条件.事件 A 可以理解为:在第 k 次取红签,有a种取法;在其他k-1次,是从a+b-1根不同的签中任取k-1根的全排列,共有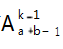 种方法,即事件A含有
种方法,即事件A含有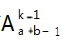 个样本点,由古典概型公式可得;
个样本点,由古典概型公式可得; 
