高中数学习题课变式教学探索—以“ 函数的概念与基本性质”习题课为例论文

SCI论文（www.lunwensci.com）

　　摘  要：新课程改革明确了高中数学基本的教学思想与形式，即使用教材传授知识与利用教材 习题组织开展教学活动．而随着我国教育事业的不断发展，如今，越来越多的教学方法被运用到了 高中数学教学之中，变式教学便是广受教师好评的教学方法之一，许多教师在运用了变式教学后均 获得了较为满意的教学成果．对此，教师也可尝试将变式教学与习题课联系到一起，以帮助学生在 感知新知本质的同时把握数学学习的规律，从而发展其数学核心素养．本文将围绕人教版高中数学 《 函数的概念与基本性质》章节，就变式教学方法的具体运用策略展开探讨.

　　关键词：高中数学；习题课；变式教学

　　《 函数的概念与基本性质》是函数部分的基础  内容，无论是初中还是高中数学，函数均占有极其重  要的地位．到了高中阶段，函数的抽象性陡然上升， 为帮助学生理清函数各变量之间的关系，教师可以  在讲解习题时采用变式教学法，借变式挖掘函数本  质的同时还能引导学生展开深入地交流与探讨，继而发展学生的数学核心素养.

　　1 课标解读

　　高中数学的《 函数的概念与基本性质》章节的  主要教学目标是让学生构建出函数知识体系，以此  促使学生从变量变化的对应关系上升到集合的集合  论描述中，继而让学生的思维从直观感知过渡到抽  象归纳之上．与此同时，在学生学习函数的过程中， 教师还应指引学生借助对函数性质特征的分析去合理构建函数模型，逐步掌握解决函数问题的方法.

　　2 学情分析

　　学生在高中阶段已接触到了集合与集合表达方 法等知识，也了解了集合与元素之间的基本关系，有 了以上基础，便能独立完成集合间的交、并、补混合 运算，且对数学化归、转化等数学思想有了一定程度 的了解，可借助数形结合或分类讨论的方式去解决 几何问题.

　　3 教材内容分析

　　函数作为高中数学的重点学习内容之一，无论 是基础概念还是性质特征，均是高中学生需要攻克 的难关．同时，函数在构建完善数学知识体系及培养 学生数学思想方面也发挥着无可替代的重要作用.  因此可以说，学生能否全面掌握函数的基本概念，领 悟函数的性质特征，将直接关系到学生数学核心素养及能力水平的发展．在学习了函数的基本概念与 性质之后，学生还将面临更为高深的函数模型等知 识，这些均对学生的函数学习基础有着极高要求．由 此可见，函数知识对学生整个高中阶段的学习均有 着重要影响.
 

　　4 教学设计

　　4. 1 教学目标

　　基于上文分析，本文在研究的过程中主要是针  对人教版高中数学《 函数的概念与基本性质》这个  章节的内容进行具体教学，共计提出了五大教学目  标．分别是：能够使用数学语言准确描述函数概念； 明确函数的三要素并能求解函数解析式；能够说明  简单函数的定义域与值域；能够准确判断一般函数  的奇偶性以及掌握在坐标系上绘制函数图像的方  法．基于以上目标，可以明确本章节的教学重点是： 理解函数的基本概念及表达方法；识别函数的奇偶  性与单调性；了解分段函数的实质并掌握处理分段  函数的方法.

　　基于以上教学重点，可确定教学难点主要包括 证明函数的奇偶性与单调性；利用函数性质解决实 际问题.

　　4. 2 教法分析

　　采用变式教学法进行本章节教学，教师需首先 结合学生学情与上述教学目标对经典函数习题予以 合理的变式处理，随后向学生下达任务，以任务来驱 动教学，如此既能彰显学生在学习中的主体地位，又 能全方位锻炼学生独立思考、合作交流等数学核心 素养，进一步促使学生理解函数概念及性质的同时 掌握应用性问题的解决方法.

　　4. 3 教学案例

　　4. 3 . 1  习题一

　　奇偶性是高中函数知识的基础性内容，也是学 生最先接触到的函数知识．教师在对此部分知识及 相关习题做变式处理时也要充分考量学生当前对知 识的认知程度，确保变式的合理性．首先，教师可从 两个基础性的问题入手，通过对基础问题的变式教学为后续教学打下基础．如第一个问题可选择人教 版高中数学教材必修一 中的练习题，题目内容为：已知函数 f( x ) 为偶函数，且在(0 , + ∞ ) 上为减函数，试判断函数f( x ) 在( - ∞ , 0) 上的单调性并证明.

　　分析  该题具有一定的探究性，对于学生总结  数学思想方法，构建函数知识体系均有一定帮助．基  于此题仅考查了证明函数奇偶性与单调性的方法， 故整体的难度系数较低，学生解答时能深化其对函数基本概念的理解.

　　变式 1   f( x ) 在(  - ∞ , 0) 上为单调递减函数，在(0 , + ∞ ) 上为单调递增函数，试判断函数f( x ) 的 奇偶性.

　　设计意图：变式 1 采用的逆向变式方法，目的既 是为了锻炼学生的辩证思维，也是为了能强化学生 对函数性质的理解，进而促使学生学会从具象的函 数图像中得出抽象数学结论的方法.

　　变式 2    函数f( x ) 为奇函数，已知该函数在(0 ,+ ∞ ) 上是增函数，判断函数 f( x ) 在区间( - ∞ , 0)上的单调性.

　　设计意图：变式 2 是通过改变条件的方式完成 了变式，目的是为了让学生能够在探究函数奇偶性 与单调性的同时还能理清它们之间的逻辑关系．对 此，教师讲解习题的过程也可选择典型函数，引导学生 经历思维从具象到抽象、从特殊到一般的发展过程.

　　变式 3    已知函数 f( x ) 为偶函数，该函数在( - ∞ , 0) 上为减函数，试判断其在(0 , + ∞ ) 上的单调性.

　　设计意图：此变式为典型的类比变式，虽然在原 题上作出了拓展并改变了题中已知条件，但解决的 思路基本一致.

　　变式 4    函数 f( x ) 的定义域为 R , 其在定义域  上为偶函数．已知 f( 4 )  < f( 3 )  < 0 , 试判断 f( 7 ) 、 f(8) 与f(5) 、f(3) 的大小关系.

　　设计意图：此变式重点考查了学生利用函数奇偶 性解答问题的能力，目的是要让学生掌握函数性质的 应用方法，进而深化其对函数值间逻辑关系的认知.

　　变式 5   偶函数在对称区间上的单调性是相同的，请判断并证明此命题的真假.

　　设计意图：该变式为一般变化式，问题以命题的 形式提出．学生在解答该问题时还能同步探知函数 性质，在强化学生的逻辑思维的同时还能引导学生 理解函数的本质.

　　变式 6    (1) 已知偶函数f( x ) 在[ m , n ] 上为增函数，试问该函数在[ - n , - m ] 上是增函数还是减函数？ (2) 已知奇函数 g( x ) 在[ m , n ] 上为减函数，则该函数在[ - n , - m ] 上是增函数还是减函数？

　　设计意图：变式 6 是以变式 5 为基础的，通过对 变式 5 的一般化解释进行变式求解训练，加深了学 生对函数性质和区间概念的认知与理解.

　　4. 3 . 2 习题二

　　人教版高中数学教材中还有一道适合变式训练 的习题，原题为：函数f( x ) 的定义域为 R , 已知该函 数在其定义域上是奇函数，当 x≥0 时，f( x ) = x (1 +  x ) , 请画出函数f( x ) 的图像并求该函数解析式.

　　分析  此题难度系数较低，主要考查了学生对 函数奇偶性的掌握.

　　变式 1    已知函数 f( x ) 的定义域为 R , 该函数在定义域上为奇函数，当 x≥0 时，f( x )  = x ( x - 2) ,试求函数f( x ) 的解析式.

　　变式 2    已知函数 f( x ) 的定义域为 R , 该函数 在定义域上为偶函数，当 x≥0 时，f( x )  = x (2 + x) , 试求函数f( x ) 的解析式.

　　设计意图：变式 1 与 2 均利用了类比变式的方 法，分别对条件及结论作出了改变，目的是为了考查 学生对分段函数奇偶性的掌握情况.

　　变式 3    已知函数f( x ) =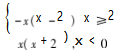, 试判断函数f( x ) 的奇偶性.

　　变式4    已知函数f( x ) 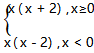 =, 试判断函数f( x ) 的奇偶性.

　　设计意图：此题意在锻炼学生的逆向思维及数 形结合思想的运用，本题不仅能让学生意识到运用 数形结合思想的重要性，当学生在图像帮助下获得 问题的正确答案后，还能强化学生的学习自信.

　　变式 5    函数 f( x ) 的定义域为 R , 该函数在其 定义域上为奇函数，当 x≤0 时，f( x )  = x (1 + x) , 请 画出函数图像并求该函数解析式.

　　设计意图：此变式主要考查了学生的类比思维， 尽管题目不甚新颖，但能解答出该问题，表明学生已  经掌握了该知识点，进而也为学生后续独立设计变  式问题打下了坚实基础.

　　变式 6    函数 f( x ) 的定义域为 R , 且该函数在其定义域上为偶函数，当 x≥0 时，f( x )  = x ( x - 1) .已知方程f( x ) - m = 0 仅有一个实数根，则 m 的取值范围应当满足怎样的条件？

　　设计意图：该变式不仅要求学生懂得如何利用 图像去求解函数的解析式，还要会运用数形结合的 思想将函数与方程联系到一起，借此让学生意识到 函数与方程有着并存的关系，故此变式也是在原题 基础上的类比变式.

　　5 结论

　　总之，高中数学以变式的方法开展习题教学 不仅能帮助学生深入探寻问题的本质，还能深化 学生对知识的记忆与理解．因受传统应试教育教 学理念的影响，绝大多数高中数学教师仍旧习惯 于沿用题海战术．然而，一 味地解题并不能提高学 生的解 题 技 巧，且 容 易 激 起 学 生 的 厌 烦 心 理．因 此，教师必须结合变式教学思想，将经典问题与变 式结合在 一 起，以此才能在激活学生辩证思维的 同时激发他们的学习动力，进而为培养学生的数 学核心素养打下坚实基础.

　　参考文献：

　　[1]  雷洪春．高中数学习题课变式教学探索— 以“ 函数的概念与基本性质”习题课为例[ J] . 华夏教师，2022(25) : 43 - 45 .

　　[2]  詹增春．略谈高中数学习题讲评课的变式教学 [ J] . 考试周刊，2015(94) : 3 .

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/70632.html