SCI论文(www.lunwensci.com)
摘 要 : 本文为探究隐含条件助力数学解题,以不等式为例,分别对已知方面、推理方面、定义 方面、联系方面、认知动因方面以及图形方面对不等式隐含条件解答方法进行了阐述,为发掘隐含 条件助力数学解题.
数学问题的完整性通常包括条件和目标,问题 条件则又包括显性条件、隐性条件和显性干扰条 件,这些条件对数学解题起到了很大的作用.一般 隐性条件容易被忽略,所以需要学生自己去发掘 ; 干扰项会增加试题的难度,从而影响学生 的思维 设定.在解题时,学生只需要确定显性条件,挖掘 隐藏的条件,排 除干扰,就能提高解题 的效率.从 高中数学试题模块的角度来看,不等式一般都是 与数列、函数、导数等知识结合在一起,甚至作为 压轴题型出现,并且压轴题具备一定的难度,如果 学生能够清楚地解决问题,并且能够找到 问题突 破口,那么解决问题便可水到渠成.此外,在选择 题和填空题 中,也会出现不等式,所 以,我们要注 意对不等式解题规律进行归纳和总结,以便为高 考做好充分的准备.
1 已知方面: “焦点”解题
学生们在解题的时候,要做的就是将老师教给 他们的知识进行扩展,要想知道这些问题的答案,就 必须对现有的条件进行深入分析和归纳,然后才能 得出答案中的隐含条件.
从分析中可以看出,问题的关键是如何利用好已知条件,并将问题隐含的条件转化为已知的条件, 并从中找出问题的中心,即“| AB | = 60 ”.在找到了 解题的关键点后,这个问题就从一个不完全的问题 转变为一个简单的不等式问题,从而大大减少了解 题的困难.
2 推理方面: “对偶式”解题
在高中数学教学中,只要掌握了一些方法,就可 以显著地减少试题所包含的隐性条件,从而彻底地 解决数学问题.只有通过对问题的不断思考和推理, 学生们才能找到问题的答案,并且找到答案所需要 的问题条件.
当学生们看到这道题的时候,他们的第一反应 就是这道题的难度大,题干所给出的条件不够,难以 进行推理与求证,但是如果能够通过合理的逻辑推 理,就能发现这道题的隐含条件.
解析 挖掘隐含条件,构造对偶式,令
从以上问题的分析可以看出,单靠题干的显性 条件很难展开目标论证,因此需要学生充分发挥自 己的能力,理解题中的隐含条件,就像前文提及的数 学题型,该类题型在高学数学教学中“出镜率”较 高,但也存在着一定的困难,这类题型的目的是为了 考验学生知识储备量,只有掌握了不等式固定关系,方可有效解决数学问题,以达到“补全”的目的.学 生在未来的学术研究中,要想得到未知的知识,就必 须要有这样的“补全”思想,将所学知识和已知条件 结合起来,这样才能更好地解决一个数学问题,所以, 在学习和练习这些问题的时候,教师就需要给学生提 供一个很好的学习机会,并在一定程度上对其进行引导,以此作为他们在日后学习和工作的前提保障.
3 定义方面: “一次函数具有单调性”解题
数学解题过程中,相关定义与属性是解决问题 的起点,作为一类较为简单的隐含条件,如果没有得 到充分关注,它也有可能会变成难以被挖掘的隐含条件.
通过以上分析可以看出,在做题的时候,如果学 生及时发现此类隐含关系,那么总体计算并不困难,因此要求老师在平时的训练中要对学生进行引导,并引导他们进行相应的积累.在要求学生进行推理 操作时,要注意给学生指明问题的关键,以便使他们 能够找到隐藏的情况,避免让他们进行死记硬背.
5 认知动因方面: “两个正数的和大于 0”解题
在数学教学中,既有教学的认知动机,又有激发 学习内容与学习方法的策略.前半部分内容揭示联 想,后半部分内容揭示类比,因此数学解题过程既包 含了联想又包括了类比.
从这一类问题的解题过程来看,这类问题是一 个很好的测试题干分解能力的题目,老师在给学生讲 解完问题后,要着重分析它的隐含条件的特点,这样才 能引起学生的注意,从而在后面的解题中发现问题.
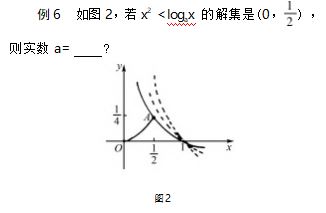
6 图形方面: “函数的图象”解题
数学代数与几何一旦分道扬镳,它们的发展就 会非常缓慢,而且它们的用途也会变得很有限,但如 果它们结合起来,互相补充,互相促进,就能起到共 同进步的效果.在不等式解题中,也应如此,我们应 将题干与图象相互结合,充分挖掘隐含条件.
数形结合是数学发展的一个重大发现,同时也 是目前高中数学试题中发现隐含条件的最佳工具, 所以,在教学过程中,教师要充分地训练学生将图形 联系题干.另外,由于高中数学的功能模块化,使学 生对函数的理解能力得到了提高,因此,在日常教学 中,老师要强化学生对图形的理解,让学生在一定的 时间内完成函数图形的绘制,或者让学生编写相应 的函数图形.
总而言之,如若在解决不等式问题时忽略题干 的隐含条件,很可能会导致问题解决出现失误,所 以,在解决不等式问题时,要注意对问题的深入挖 掘,这样才能保证解题的精确性和严密性.在目前高 中数学试题中,不等式问题的解题形式和知识点都 比较丰富,解题的方法也很多,但通常情况下解题的 难度并不大,如果不能将不等式和相应定义等内容 结合起来,则会影响对题目开展论证与运算,从而影 响整体学习效果.
参考文献 :
[1]俞梅清.高中数学解题中隐含条件的挖掘[J]. 数理化解题研究,2021 (10) :20-21 .
[2]赵春.高中数学解题中隐含条件的挖掘应用[J].数理化解题研究,2019(10) : 14 -15 .
[3]王乙羽.高中数学三角函数解题中的隐含条件 的挖掘[J].考试周刊,2018(30) : 67-68 .
[4]郑宇,陈明.浅谈中学数学解题中隐含条件的挖 掘[J].遵义师范学院学报,2020.22 (04) : 141
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69839.html