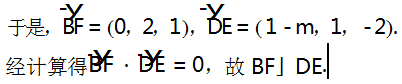SCI论文（www.lunwensci.com）:
摘要 : 本文以数形结合的理论基础为切入点，着重探索数形结合思想在 2020 －2022 年高考 全国理科卷中函数及立体几何的具体应用，以帮助学生解决复杂问题，切实提升数学解题能力.
关键词 : 数形结合思想,高考, 数学解题
1 数形结合思想
数形结合思想是高中数学中学生必须要掌握的 思想方法，它体现在高中数学内容的各个方面，如集 合、不等式、向量、三角函数、解析几何、立体几何等. 通过阅读大量文献发现，许多学者对“数形结合”都有自己的理解.
徐文龙把“数”理解为数学文字表征，即数字、 数学概念、数学定理、数学结构等，把“形”可以理解为图形表征，即实物、图象、图表、图形等.
蔡小雄认 为“形”因“数”得到抽象的概括， “数”因“形”得到直观的体现，将数学语言与图形语 言巧妙结合，利用图形的直观刻画和代数的严谨论证，使数学问题得以研究和解决.
华罗庚在描述数形结合时说: “数缺形时少直 观，形缺数时难入微．数形结合百般好，割裂分家万事休. ”
2 数形结合思想在2020－2022 年高考全国理 科卷中的应用
经过对近几年高考试题的研究，在解决一些复 杂的问题时运用数形结合的思想方法，可以小费力 获得大收获，特别是在求解选择题、填空题中更能表 现出它的优越性．在这里主要以“函数”“立体几何”这两类较难的问题进行探索.
2．1 在函数问题上的应用
函数是高中数学学习中的重点与难点，是高中 数学课程内容的四条主线之一，在高中数学中占据 非常重要的地位．在解决函数问题时，可以应用数形结合思想，将题目中的问题与图形有效结合起来，通过图形将题目中的问题具体化，抓住题目中的解题要点.
例 1 (2022 年全国乙卷) 已知 x = x1 和 x = x2 分 别是函数f ( x) = 2ax －ex2 ( a＞0 且 a≠1) 的极小值点 和极大值点．若 x1 ＜x2，那么 a 的取值范围是 _ .
解析 由题意，得f '( x) = 2axlna－2ex(a＞0 且 a≠1) ，因为 x = x1 和 x = x2 分别是函数f ( x ) 的极小值 点和极大值点，即f ' ( x ) = 0 有两个不同的实数根 x1 ，x2 ，且 x1 ＜x2 .
当f '( x) = 0 时，ax =
x，令 g ( x) = ax，h ( x) =
x，则g( x) 与 h( x) 的函数图象有两个不同的交点.
当 0 ＜a ＜1 时，g '( x ) = axlna，设函数 g ( x ) 过原 点的切线方程为 y －ax0 = ax0 lna ( x－x0 ) ，如图 1 所 示，则 0 －ax0 = ax0lna ( 0－x0 ) .
即 x0 lna = 1，即 x0 =
= loga e.
所以切线斜率
，要使 g ( x ) 与 h ( x ) 的函数图象有两个不同的交点，则
＜k = elna，即ln2 a ＜1，解得
＜a＜e.
又 0 ＜a ＜1，所以
＜a ＜1.
当 a ＞1 时，若函数 g ( x ) 与 h ( x ) 的图象有两个 不同的 交 点，则函数图象如图 2 所示，则 当 x ∈ ( 0，x1 ) 时，f '( x ) ＞0，可得函数f ( x ) 是单调递增的 ; 当 x∈( x1 ，x2 ) 时，f '( x ) ＜0，可知函数f ( x ) 是单调递 减的 ; 当 x∈( x2 ，+ ∞ ) 时，f '( x ) ＞0，f ( x ) 单调递增. 则 x1 为极大值点，x2 为极小值点，与题意不符.
综上所述，a 可取的范围是
，1 ).
例2 (2021 年全国甲卷) 设 a≠0，如果x = a 是函数f( x) = a ( x－a) 2 ( x－b) 的极大值点，则( ) .
A．a＜b B．a＞b C．ab＜a2 D．ab＞a2
解析 函数f ( x ) 求导得
f '( x ) = 3a ( x－a ) (x－
.
由于 a≠0，所以对 a 进行分类讨论.
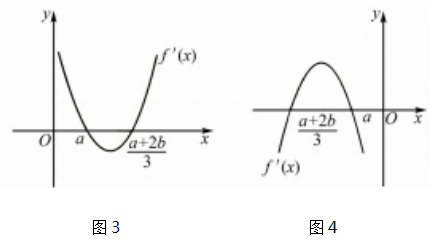
当 a＞0 时，f ' ( x ) 图象如图 3，可得 a ＜
，即 a＜b，所以 ab－a2 = a ( b－a ) ＞0，故 ab＞a2 .
当 a＜0 时，f '( x) 图象如图4，可得 a＞
，即 a> b，所以 ab－a2 = a( b－a) ＞0，故 ab＞a2．故选 D.
通过这两个例题，可以发现 : 在近几年的高考题 中，对于函数的考查主要集中在“极值”这个比较困难的知识点上．同时考查了学生的逻辑推理能力及化归与转化思想，体现了数学运算的核心素养.
2．2 在立体几何问题上的应用
在每年的高考题中，立体几何最常见的考法就 是 12 分的一道大题．对于这类题几乎有相同的步 骤，首先建立空间直角坐标系，然后巧妙地将立体几 何与空间向量相联系，最后利用数形结合思想方法来解决问题.
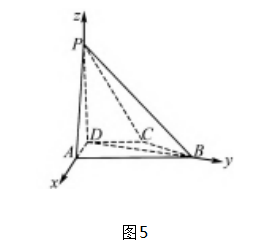
例 3 (2022 年全国甲卷) 如图 5，P－ABCD 是 四棱锥，PD⊥底面 ABCD，CD ∥AB，AD = DC = CB =1，AB = 2，DP =
.
( 1) 证明 : BD⊥PA;
(2) 求 PD 与平面 PAB 所成的角的正弦值.
解析 ( 1) 因为 CD∥AB，AD = DC = CB = 1，AB = 2，可知四边形 ABCD 是等腰梯形，易得 BP =
， 且 AD2 + BD2 = AB2 ，所以 AD⊥BD.
又因为 PD」底面 ABCD，BD军底面 ABCD，故 PD 」BD．因为 PD，AD军平面 PAD，PD nAD = D，故 BD」 平面 PAD．又因为 PA军平面 PAD，得到 BD」PA.
(2) 将 D 记作坐标原点，将 DA，DB，DP 所在直线分别记作 x，y，z 轴，建立空间直角坐标系．那么D ( 0 ，0 ，0 ) ，A ( 1 ，0 ，0 ) ，B ( 0 ，
，0 ) ，P ( 0 ，0 ，
) .
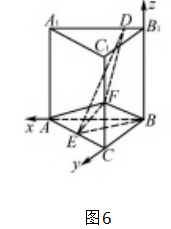
例4 (2021 年全国甲卷) ABC－A1 B1 C1 是直三棱 柱，侧面AA1 B1 B 是正方形，AB = BC = 2，E，F 分别为AC 和 CC1 的中点，D 为棱A1 B1 上的点，BF」A1 B1 .
( 1) 证明 : BF」DE;
(2) 平面 BB1 C1 C 与平面 DFE 所成的二面角的 正弦值最小时，B1 D 取何值?
解析 ( 1 ) 因为 E，F 分别为 AC 和 CC1 的 中 点，侧面 AA1 B1 B 是正方形，AB = BC = 2，所以 CF = 1，BF =
，如图 6 所示，连接 AF，由 BF 」A1 B1 且AB/A1 B1 ，则 BF」AB．故 AF = 3．所以 AC =
.
由 AB2 + BC2 = AC2 ，则 AB」BC.
故以 B 为坐标原点，
, 所在的方向分 别为 x，y，z 轴的正方向建立空间直角坐标系．于是A( 2，0，0 ) ，B ( 0，0，0 ) ，C ( 0，2，0 ) ，E ( 1，1，0 ) ，F( 0，2，1 ) ，设 B1 D = m，则 D( m，0，2 ) .
(2) 因为 AB 」BC，侧面 AA1 B1 B 为正方形，则 AB」BB1 ，且 BC n BB1 = B．故 AB」平面 BB1 C1 C.
通过这两个例题，可以发现 : 在近几年的高考题 中，对于立体几何大题的考查主要集中在证明线线 的关系及求线面所成角上．考查了学生的空间想象能力、运算求解能力，体现了直观想象的核心素养.通过对 2020 －2022 年高考全国理科卷中个别 题目的详细解答可以发现 : 现在的高考数学不仅仅 是对知识点的考查，考查更多的是学生的逻辑推理、 直观想象等能力．所以，在教学过程中，首先增强学 生的学习兴趣，其次在进行思想方法渗透时要有支撑，最终提高学生运用数形结合方法解决问题的能力.
参考文献 :
［1］蔡小雄．更高更妙的高中数学思想与方法［M］.杭州: 浙江大学出版社，2012 .
［2］ 陶政国．论数形结合思想在高中数学解题中的 优势与应用［J］．数理化解题研究，2022 ( 16)
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/69762.html
